Distance measure for textures

In this work we have chosen the Kullback distance between two Gaussian models of textures :

$$\begin{array}{r} D(P_{1},P{2})=\frac{1}{2}(\mu_{2}-\mu_{1})... ...\sum_{1}^{-1}\sum_{2}+\sum_{1}\sum_{2}^{-1}-2I)\\ \end{array}$$

Clearly, one is interested in being able to define a distance measure, which is invariant to translation and rotation.To achieve the desired invariance, we have implemented the following procedure:

• Estimate the parametric model of each texture patch.
  

• For textures with harmonic components, the texture is first rotated so that its dominant harmonic component is aligned with a predefined direction (the x-axis, for example).
  

• For textures with evanescent components, the dominant evanescent component is considered the one whose modulating 1-D purely-indeterministic processes have maximal variance. Thus, the texture is first rotated so that its dominant evanescent component has $(\alpha,\beta)=(1,0)$.
  

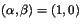• For textures with harmonic components where the phase of the dominant component is not zero, we crop a sub-picture of the original in which the phase of the dominant component is zero.
  

• Re-estimate the texture parameters to find the parameters of all the model components.
  

  

Figure: Textures ordered using the Kullback distance. The test texture is structured, dominantly harmonic.

Test Texture

The Kullback distance is computationally expensive. Therefore we derived a hierarchical approach :

• if both textures are deterministic : the distance becomes the euclidean norm between spectral densities
  

  $$d=\Vert s_{1}-s_{2}\Vert _{2}$$

  
  

• if both textures are purely random : the distance is reduced to the Itakura-Saito distance
  

  $$d=\left\vert \left\vert \frac{s_{1}}{s_{2}}-\log \frac{s_{1}}{s_{2}} \right\vert \right\vert _2$$

  
  

• if one texture is purely random and one texture is deterministic : the distance is infinity

  

Figure: Textures ordered using the hierarchical distance. The test texture is structured, dominantly harmonic.

Test Texture