The 2D-Wold decomposition for textures

The texture field, $\{y(n,m)\}$ is decomposed as follows :

$$y(n,m)=w(n,m)+h(n,m)+\sum_{(\alpha,\beta )\in O}e_{(\alpha,\beta)}(n,m)$$

$\{w(n,m)\}$ : random component (w.r.t. granularity)
$\{h(n,m)\}$ : harmonic component (w.r.t. repetitiveness)
$\sum_{(\alpha,\beta )\in O}e_{(\alpha,\beta)}(n,m)$ : generalised evanescent component (w.r.t directionality)

The random component can be written as :

$$w(n,m)=-\sum_{(0,0)<(k,l)}a(k,l)u(n-k,m-l)$$

$\{u(n,m)\}$ is the 2D innovation which is a white noise with variance $\sigma ^{2}$

The harmonic component is given by :

$$h(n,m)=\sum_{p=1}^{P}(C_{p}\cos2\pi(n\omega_{p}+m\nu_{p}) +D_{p}\sin2\pi(n\omega_{p}+m\nu_{p}))$$

C_p,D_pare mutually orthogonal random variables

The evanescent component can be expressed :

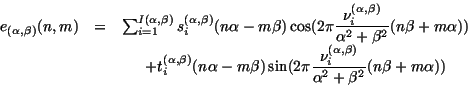$$\begin{array}{lcc} e_{(\alpha,\beta)}(n,m) & = & \sum_{i=1}^... ...,\beta)}}{\alpha ^{2}+\beta ^{2}}(n\beta+m\alpha)) \end{array}$$

s_i,s_j,t_k,t_l are 1-D random proceses mutually orthogonal for all $i,j,k,l,i\neq j,k\neq l$