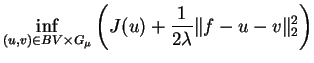 |
(2.9) |
| (2.10) |
The parameter ![]() controls the
controls the ![]() norm of the residual
norm of the residual ![]() .
The parameter
.
The parameter ![]() controls the
controls the ![]() norm of
norm of ![]() . The larger
. The larger ![]() is, the more
is, the more ![]() contains information.
contains information.
Remark:
We have
![]() .
.
Principal: We solve the two following problems:
![]()
![]() being fixed, one solves
being fixed, one solves
The solution of (2.11) is given by:
| (2.12) |
![]()
![]() being fixed, one solves
being fixed, one solves
The solution to(2.13) is given by:
| (2.14) |
Algorithm: To solve problem (2.9), we iteratively solve problems (2.11) and (2.13).
1) Initialization:
| (2.15) |
2) Iterations:
| (2.16) |
| (2.17) |
3) Stopping test: we stop when
| (2.18) |
Discretization:
Our image is a two dimensional vector of size
![]() . We denote by
. We denote by ![]() the Euclidean space
the Euclidean space
![]() .
.
We want to find:
Lemme
2.2. There exists a unique couple
![]() minimizing
minimizing ![]() on
on
![]() .
.
Convergence of the algorithm:
Proposition
2.3. The sequence
![]() converges to the minimum of
converges to the minimum of ![]() on
on
![]() .
.
Recall of Meyer's problem: We thus consider:
Link with Meyer's problem:
Our limit problem is:
![]() Let us set
Let us set
![]() in Meyer's problem (2.22). Then we can choose
in Meyer's problem (2.22). Then we can choose
![]() so that Meyer's problem (2.22) and our limit problem (2.23) have the same solutions.
so that Meyer's problem (2.22) and our limit problem (2.23) have the same solutions.
Role of ![]() :
:
We recall that our problem is:
![]() Let us denote by
Let us denote by
![]() the solution of our problem (2.24).
Then
the solution of our problem (2.24).
Then
![]() converges to
converges to
![]() (when
(when ![]() goes to 0) solution of our limit problem
(2.23).
goes to 0) solution of our limit problem
(2.23).