(Physica D. 1992)
Definition
1.1.
![]() is the subspace of functions
is the subspace of functions ![]() in
in
![]() such that the following quantity is finite:
such that the following quantity is finite:
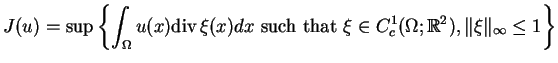 |
(1.1) |
Remark: if
![]() , then
, then
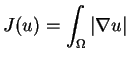
In the ROF model, one seeks to minimize:
Chambolle's model: A. Chambolle has proposed a projection algorithm to minimize the total variation (MIA 2002).
Proposition 1.1. The solution of (1.2) is given by:
Meyer's model :
Y. Meyer (2001) has proposed the following model:
The Banach space ![]() contains signals signals with strong oscillations, and thus in particular textures and noise.
contains signals signals with strong oscillations, and thus in particular textures and noise.
Definition
1.2. ![]() is the Banach space composed of the distributions
is the Banach space composed of the distributions ![]() which can be written
which can be written
| (1.6) |
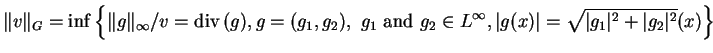 |
(1.7) |
Exemple:
| Images | |
|
|
| textured image | 1 000 000 | 9 500 | 360 |
| geometric image | 64 600 | 9 500 | 2000 |
Remarks:
Lemma
1.1.
![]() and
and
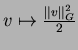 are dual (in the sens of the Legendre-Fenchel duality).
are dual (in the sens of the Legendre-Fenchel duality).
Proposition
1.2. In the discrete case, the space ![]() identifies with the following subspace:
identifies with the following subspace:
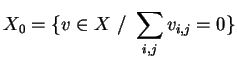 |
(1.8) |