Partition, level set approach
The image is considered as a function
![]() (where
(where ![]() is an open subset of
is an open subset of
![]() )
)
We denote
![]() .
The collection of open sets
.
The collection of open sets
![]() forms a partition of
forms a partition of
![]() if and only if
if and only if
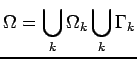 , and if
, and if
In order to get a functional formulation rather than a set formulation, we suppose that for each
![]() there exists a lipschitz function
there exists a lipschitz function
![]() such that:
such that:
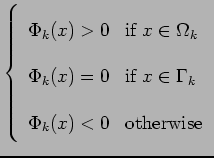
Regularization
In our equations, there will appear some Dirac and Heaviside distributions ![]() and
and ![]() .
In order that all the expressions we write have a mathematical meaning, we use the classical regular approximations of these distributions (see figure 2):
.
In order that all the expressions we write have a mathematical meaning, we use the classical regular approximations of these distributions (see figure 2):

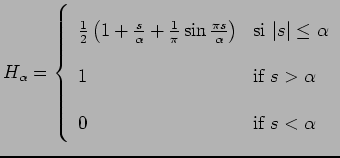
Figure 3 shows how the regions are defined by these distributions and the level sets.
Functional
Our functional will have three terms:
1) A partition term:
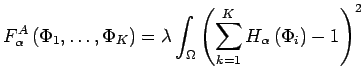 |
(2.1) |
2) A regularization term:
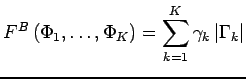 |
(2.2) |
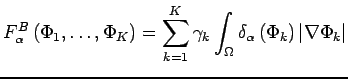 |
(2.3) |
3) A data term:
| (2.4) |
The functional we want to minimize is the sum of the three previous terms:
| (2.5) |