Previous : Point processes Up : Contents Next : Algorithm


Urban area model

We aim at detecting buildings on a DEM. We propose to first detect silhouettes of buildings, and then to estimate their 3D shape. To achieve this, we model silhouettes of buildings by rectangles.

Our goal is then to detect an unknow number of rectangles on the DEM. We define a process of rectangles and we built its energy using two parts.

  • The first one is an internal field reflecting the knowledge we have on how buildings interact in urban aera,
  • the second one is an external field telling for a proposed silhouette if it is relevant or not on the DEM.

Working on S, the space representing rectangles, we introduce a point process with the following density against the reference marked Poisson point process of intensity vS.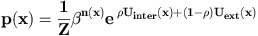



rho is a smoothing factor living in ]0,1[. Our goal is to maximize this density. This has been down several times, especially in image processing (see [1,16,17]).

Figure i) The energy defined for configurations of rectangles we want to minimize is a ponderation between two terms.

An internal field :




and an external field :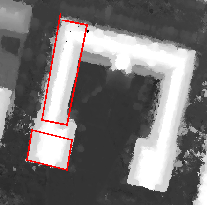


Internal field

They are several models available to deal with interactions between the points of a point process. The simplest one is the pairwise interaction model. We have done some work to introduce others model (see [14]) allowing to deal with interactions involving more than two points. But results presented here were obtained with simple interactions.

A pairwise interaction model is defined by a symmetric relation between points ~ , and by an energy under the following form :



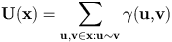where gamma is a potential function. In the density of point processes section, the relation used was the proximity one, and the potentiel function was equal to V.

Results presented here were obtained using only the intersection relation (two rectangles are in interaction iff their intersection is non empty), and with a potentiel function equal to 1. This makes intersections be rejected.

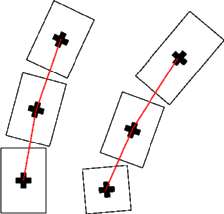
We have also done some tests using other kind of relations, like alignements, orthogonality and proximity with non constant potential functions.

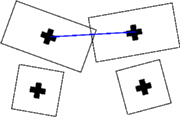
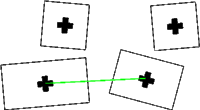
Figure j) We present here some of the interaction that we have used or tested and the effect of associated potential functions.

Proximity Homogeneous close buildings are favourised.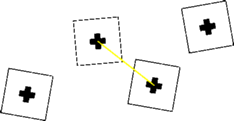

Intersection Intersecting buildings are penalised.

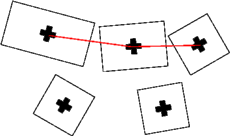
Alignement Aligned buildings are favourised (two or three points interaction term) with potential functions minimized if alignement is good and distance between interacting buildings small.


External field

The external part of the energy ensures that the density favourise silhouettes of builings that are relevant on the DEM.

We use an external field written like :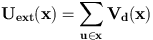



where Vd is an intensity potentiel rating how relevant a building u is. We have two contraints on how Vd should behave. First, minima of Vd should be relevant buildings on the DEM. Secondly, the function should be quite smooth to ease the optimisation.

An other kind of external field can be used. It gives better results, but our algorithm become quite slow while using it. This other external field consist in a distance between the data DEM, and a reconstruction of the DEM made from a configuration of rectangles.

Our intensity function uses a ground estimate : for a proposed building, we estimate the heigh of the ground around it. We then look at three different rates, all living in [0,1].

  1. the first rate is a volume rate v. We look at the points of the DEM living inside the proposed building and watch if they are higher than the ground estimate augmented by a real parameter h_min. The ratio of the number of points above the limit over the total number of points gives the volume rate.

  2. the second rate is an homogeneity rate t . It comes from two assumptions : heights are iid along any length way axis. And buildings are symmetric with respect to the median length way axis.

  3. the last rate is a surface rate s . It is the ratio between the surface of u and the maximum surface of a rectangle Lmax*lmax

The three rates are the mixed to give a reward function J(.), by mean of a geometrical ponderation.



The behavior of this reward function is presented by Figure h). The reward function is directly involved in the intensity function Vd. We use three positive real parameters a,b and v_min that make Vd live in [-a,b].



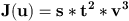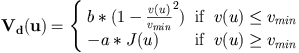 Figure h) We present here how the reward function behave.

is here an extract of a DEM. (by cliquing, you get the third dimension)



And here from left to right, three proposition are ordered with increasing reward function.
Previous : Point processes Up : Contents Next : Algorithm



Back to M. Ortner's home page !