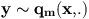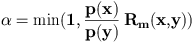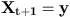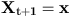| Previous : Urban area model | Up : Contents | Next : Results |
|
||
|
We have defined a probabilist model for urban aeras. The estimate we
use is the configuration of rectangles that maximises the density
previoulsy built. The algorithm used is a sampler, coupled with a simulated annealing. |
||
|
||
|
We use a MCMC method. The sampler we built is a
Hastings-Metropolis-Green one. The basic idea underlying this sampler
has been proposed and justified by Geyer and Moller (see [8])
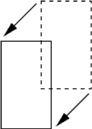
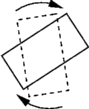
We built a Markov Chain that converges ergodicaly to the distibution we have defined by its density. Hastings Metropolis algorithm use a proposition kernel and an acceptance rate. Proposition kernelWe first need a proposition kernel. It corresponds to stochastic perturbations that can be applied to a given configuration of rectangles. The perturbations we have implemented can be divided into two class :
 Green ratioIf we apply one of the kernels q_m to a configuration x, we obtain a new configuration y. We then have to compute a ratio, depending on x and y.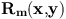 AlgorithmThe algorithm can be described a following. We suppose we want to sample a point process according to the density p(.)Given a configuration of points : 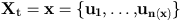
|
Figure k) . Perturbations kernels T,R,DL and Dl.
  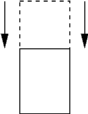 
| |
|
||
Once a sampler has been defined, it is possible to optimize the
density, using simulated annealing, as described by Winkler
in [26]. A good overview on simulated annealing techniques
can be found in [23].
We replace the density p(.) by a time depending
density. We replace U(.) energy associated to the density, by :
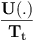 In theory, if we use the above sampler and make simoultaneously decrease the temperature from a starting value to 0 using a logarithmic law, the chain converges in total variation to a Dirac measure whose mass is equally distributed on the global minima of U(.). In practice, we use faster decreasing scemes. |
| Previous : Urban area model | Up : Contents | Next : Results |