-
Y suit la distribution du bruit gaussien
N (
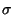 ),
N=Y-HX :
),
N=Y-HX :
| Précédent : Choix de l'estimateur Suivant : Dérivées de la log-vraisemblance |
|
|
Expression des différentes probabilités :
- Y suit la distribution du bruit gaussien N (
), N=Y-HX :
- Distribution a priori de X :
C'est une probabilité gibbsienne, car X est un champ de Markov.
![]() La vraisemblance
de
La vraisemblance
de ![]() ,
, ![]() s'écrit finalement :
s'écrit finalement :
Z, ZY = fonctions de partition (cf. physique statistique) ,
ce sont des constantes de normalisation.
est l'ensemble des images
, M niveaux de gris.
: minimum
:
Impossible de calculer directement les fonctions de partition !
à cause de la dimension de l'espace.
On ne cherchera donc pas à les calculer, mais à les estimer.