GEOMETRIC AND TOPOLOGICAL METHODS IN MACHINE LEARNING

Description

Data analysis is the process of cleaning, transforming, modelling or comparing data, in order to infer useful information and gain insights into complex phenomena. From a geometric perspective, when an instance (a physical phenomenon, an individual, etc.) is given as a fixed-sized collection of real-valued observations, it is naturally identified with a geometric point having these observations as coordinates. Any collection of such instances is then seen as a point cloud sampled in some metric or normed space.

This course reviews fundamental constructions related to the manipulation of such point clouds, mixing ideas from computational geometry and topology, statistics, and machine learning. The emphasis is on methods that not only come with theoretical guarantees, but also work well in practice. In particular, software references and example datasets will be provided to illustrate the constructions.

For any questions or concerns please contact Jean-Daniel Boissonnat at Jean-Daniel.Boissonnat[at]inria.fr, Mathieu Carrière at mathieu.carriere[at]inria.fr, or Frédéric Cazals at frederic.cazals[at]inria.fr

Outline

Class 1

Nearest neighbors in Euclidean and metric spaces: data structures and algorithms

Summary

For data modeled as a point cloud, reporting the nearest neighbors (NN) of a given point is a fundamental operation consistently reused in data analysis and machine learning, e.g. in classification and regression. Efficient NN search methods will be reviewed, both for Euclidean and metric spaces.

Keywords

Kd-trees, random projection trees, metric trees, search strategies.

Slides

Bibliography

• (book) Har-Peled, S. Geometric Approximation Algorithms. Mathematical Surveys and Monographs, AMS, 2011 (chapters 17 to 20).
• (book) Shakhnarovich, G., Darrell, T., and Indyk, P. Nearest-Neighbors Methods in Learning and Vision. Theory and Practice, MIT press, 2005.
• (book) Hanan, S. Foundations of multidimensional and metric data structures. Morgan Kaufmann, 2006.
• Arya, S., Mount, D.M., Netanyahu, N.S., Silverman, R. and Wu, A.Y. An optimal algorithm for approximate nearest neighbor searching fixed dimensions. Journal of the ACM, 45, 1998.
• Marius, M., and Lowe, D. Fast Approximate Nearest Neighbors with Automatic Algorithm Configuration. VISAPP (1), 2009.
• Indyk, P., and Motwani, R. Approximate nearest neighbors: towards removing the curse of dimensionality. Proceedings of the thirtieth annual ACM symposium on Theory of computing, pages 604-613, 1998.
• Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Transactions on pattern analysis and machine intelligence, 13(4), 376-380, 1991.
• Yossi, R., Tomasi, C., and Guibas, L. The earth mover's distance as a metric for image retrieval. International Journal of Computer Vision 40.2: 99-121, 2000
• Elizaveta, L., and Bickel, P. The earth mover's distance is the Mallows distance: some insights from statistics. Proceedings Eighth IEEE International Conference on Computer Vision, IEEE, 2001.
• Ding, Z., Li, J., and Zha, H. A new mallows distance based metric for comparing clusterings. Proceedings of the 22nd international conference on Machine learning, ACM, 2005.

Class 2

Nearest neighbors in Euclidean and metric spaces: analysis

Summary

This lecture will develop selected insights / mathematical analysis related to the data structures and algorithms studied in the first lecture.

Keywords

Intrinsic dimension, randomization, concentration phenomena.

Slides

Bibliography

• Verma, N., Kpotufe, S., and Dasgupta, S. Which spatial partitions are adaptive to intrinsic dimension? UAI, 2009.
• Dasgupta, S., and Sinha, K. Randomized partition trees for exact nearest neighbor search. JMLR: Workshop and Conference Proceedings, 30:1--21, 2013.
• Vempala, S. Randomly-oriented kd Trees Adapt to Intrinsic Dimension. FSTTCS, 2012.
• Francois, D., Wertz, V., and Verleysen, M. The concentration of fractional distances. Knowledge and Data Engineering, IEEE Transactions on, 19(7), 873-886, 2007.
• Charu, A., Hinneburg, A., and Keim, D. On the surprising behavior of distance metrics in high dimensional space. Springer Berlin Heidelberg, 2001.
• Beyer, K., et al. When is nearest neighbor meaningful? Database Theory, Springer Berlin Heidelberg, 217-235, 1999.

Class 3

Computational Topology (I): Simplicial Complexes

Summary

The purpose of this class is to introduce the most basic concepts of computational topology. We will present the definitions and computations of various types of deformations of topological spaces, as well as data structures to work with a specific family of such spaces called the family of simplicial complexes.

Keywords

Topological spaces, homotopy equivalences, simplicial complexes, triangulations.

Slides

Gudhi tutorial on simplex trees

Bibliography

Class 4

Computational Topology (II): (Persistent) Homology

Summary

The purpose of this class is to present one of the main tools of topological data analysis, the (persistent) homology groups. We will present their definitions and computation algorithms, as well as their theoretical properties, some of which being open problems in the literature.

Keywords

Cech and Vietoris-Rips complexes, (persistent) homology groups, (persistent) Betti numbers, boundary reduction algorithm.

Slides

Gudhi tutorials on Alpha (Cech) and Vietoris-Rips complexes: tutorial 1, tutorial 2, tutorial 3

Bibliography

Class 5

Manifold Learning

Summary

The purpose of this class is to tackle the problem of identifying underlying manifolds on which data sets are sampled. We will present some regularity and data set sampling conditions for which manifolds can be efficiently reconstructed.

Keywords

Representation of manifolds, sampling and regularity conditions, dimensionality reduction, reconstruction algorithms.

Slides

Bibliography

• Boissonnat, J.-D., Chazal, F., Yvinec, M. Geometric and topological inference. Cambridge University Press, 2018. Link.

Class 6

Topological Machine Learning (I)

Summary

The purpose of this class is to present and explain the main descriptor of Topological Data Analysis, called the persistence diagram. We will present its definition and stability properties, and how it can be incorporated in mode-seeking and density estimation based clustering to produce the Topological Mode Analysis Tool (ToMATo).

Keywords

Persistence diagram, stability theorem, hierarchical clustering, topological clustering.

Slides

Gudhi tutorials on Vietoris-Rips persistence and ToMATo: tutorial 1, tutorial 2

Bibliography

• Cohen-Steiner, D., Edelsbrunner, H. and Harer, J. Stability of persistence diagrams. Discrete and Computational Geometry, Volume 37, pp. 103-120, 2007.
• Chazal, F., Cohen-Steiner, D., Guibas, L., Mémoli, F. and Oudot, S. Gromov-Hausdorff Stable Signatures for Shapes using Persistence. Computer Graphics Forum (proc. SGP), pp. 1393-1403, 2009.
• Chazal, F., Guibas, L., Oudot, S. and Skraba, P. Persistence-Based Clustering in Riemannian Manifolds. Journal of the ACM, Volume 60, Issue 6, pp. 1-38, 2013.

Class 7

Topological Machine Learning (II)

Summary

The purpose of this class is to explain how the persistence diagram can be incorporated in standard machine learning and deep learning methods. We will present some of the most common vectorizations and kernels that have been defined in the literature in recent years, as well as topological layers for neural nets.

Keywords

Vectorizations & kernels for PDs, neural net architectures for PDs, optimization and gradient descent for PDs.

Slides

Gudhi tutorials on kernels and neural nets: tutorial 1, tutorial 2 (you will have to compile the perslay branch of Gudhi to run tutorial 2).

Bibliography

• Chazal, F., Cohen-Steiner, D., Guibas, L., Mémoli, F. and Oudot, S. Gromov-Hausdorff Stable Signatures for Shapes using Persistence. Computer Graphics Forum (proc. SGP), pp. 1393-1403, 2009.
• Li, C., Ovsjanikov, M. and Chazal, F. Persistence-based Structural Recognition. In Proc. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014.
• Carrière, M., Cuturi, M. and Oudot, S. Sliced Wasserstein kernel for persistence diagrams. In Proc. International Conference on Machine Learning (ICML), 2017.
• Carrière, M., Chazal, F., Ike, Y., Lacombe, T., Royer, M. and Umeda, Y. PersLay: a neural network layer for persistence diagrams and new graph topological signatures. In Proc. International Conference on Artificial Intelligence and Statistics (AISTATS), 2020.

Class 8

Reeb spaces and Mapper

Summary

This class is an introduction to exploratory topological data analysis. We will present the main tools of TDA for visualizing and interpreting data sets, called the Reeb spaces and the Mapper complexes. We will also explain the most recent theoretical results about their statistical properties and robustness.

Keywords

Nerve complex, nerve theorem, Reeb graph and Reeb space, Mapper, statistics and confidence regions on Mapper.

Slides

Gudhi tutorial for gradient descent (you will have to compile the diff branch of Gudhi to run this tutorial).

Gudhi tutorial for cover complexes (you will have to compile the mapper branch of Gudhi to run this tutorial).

Bibliography

• Singh, G., Mémoli, F. and Carlsson, G. Topological Methods for the Analysis of High Dimensional Data Sets and 3D Object Recognition. SPBG (pp. 91-100), 2007.
• Carrière, M. and Oudot, S. Structure and stability of the one-dimensional Mapper. Foundations of Computational Mathematics 18 (6), 1333-1396, 2017.
• Carrière, M., Michel, B. and Oudot, S. Statistical analysis and parameter selection for Mapper. Journal of Machine Learning Research 19 (12), 1-39, 2018.
• Chazal, F., Huang, R., and Sun, J. Gromov-Hausdorff Approximation of Filament Structure Using Reeb-type Graph. Discrete & Computational Geometry 53 (3), 621-649, 2015.
• Chazal, F., Cohen-Steiner, D., Lieutier, A. A Sampling Theory for Compact Sets in Euclidean spaces. Discrete & Computational Geometry 41 (3), 461-479.

Class 9

Dimensionality reduction algorithms

Summary

Dimensionality reduction methods aim at embedding high-dimensional data in lower-dimensional spaces, while preserving specific properties (pairwise distance, data spread, etc). This lecture will overview the main techniques for linear and non-linear dimensionality reduction.

Keywords

Principal components analysis, multidimensional scaling, Isomap, t-SNE.

Slides

Bibliography

• (book) Lee, John A., and Michel Verleysen. Nonlinear dimensionality reduction. Springer, 2007.
• (book) Sariel Har-Peled. Geometric approximation algorithms. No. 173. American Mathematical Soc., 2011.
• (book) Cox, Trevor F., and Michael AA Cox. Multidimensional scaling. CRC Press, 2000.
• Tenenbaum, Joshua B., Vin De Silva, and John C. Langford. A global geometric framework for nonlinear dimensionality reduction. Science 290.5500 (2000): 2319-2323.
• Roweis, Sam T., and Lawrence K. Saul. "Nonlinear dimensionality reduction by locally linear embedding." Science 290.5500 (2000): 2323-2326.
• Coifman, Ronald R., et al. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. PNAS (102), 2005.
• Lafon, Stephane, and Ann B. Lee. Diffusion maps and coarse-graining: A unified framework for dimensionality reduction, graph partitioning, and data set parameterization. Pattern Analysis and Machine Intelligence, IEEE Transactions on 28.9 (2006): 1393-1403.
• Dasgupta, Sanjoy, and Anupam Gupta. An elementary proof of a theorem of Johnson and Lindenstrauss. Random Structures and Algorithms 22.1 (2003): 60-65.
• Frédéric Cazals, Frédéric Chazal, and Joachim Giesen. Spectral Techniques to Explore Point Clouds in Euclidean Space, with Applications to Collective Coordinates in Structural Biology. Nonlinear Computational Geometry. Springer New York, 2010. 1-34.
• Diaconis, Persi, Sharad Goel, and Susan Holmes. Horseshoes in multidimensional scaling and local kernel methods. The Annals of Applied Statistics (2008): 777-807.
• (book) Lee, John A., and Michel Verleysen. Nonlinear dimensionality reduction. Springer, 2007.
• R.R. Coifman and S. Lafon and A.B. Lee and M. Maggioni and B. Nadler and F. Warner and S.W. Zucker, Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps, PNAS 102, 205.
• S. Lafon and Y. Keller and R.R. Coifman, Data fusion and multi-cue data matching by diffusion maps, IEEE Trans. on Pattern Analysis and Machine Intelligence 28, 2006.
• S. Lafon and A.B. Lee, Diffusion Maps and Coarse-Graining: A Unified Framework for Dimensionality Reduction, Graph Partitioning and Data Set Parameterization, IEEE Trans. on Pattern Analysis and Machine Intelligence 28, 2006.
• Kannan, Ravi and Vempala, Santosh and Vetta, Adrian, On clusterings: Good, bad and spectral, J. of the ACM 51, 2004.

Class 10

Sampling high dimensional distributions with Markov chains

Summary

Sampling points from a high dimensional density of the form exp(-f(x)) is a fundamental problem arising in machine learning, Bayesian inference, statistical physics, or geometry. This lecture will review one basic algorithm to do so, and its application to computing the volume of a high dimensional polytope.

Keywords

Markov chains, Markov Chains Monte Carlo, polytope volume calculations.

Bibliography

Location

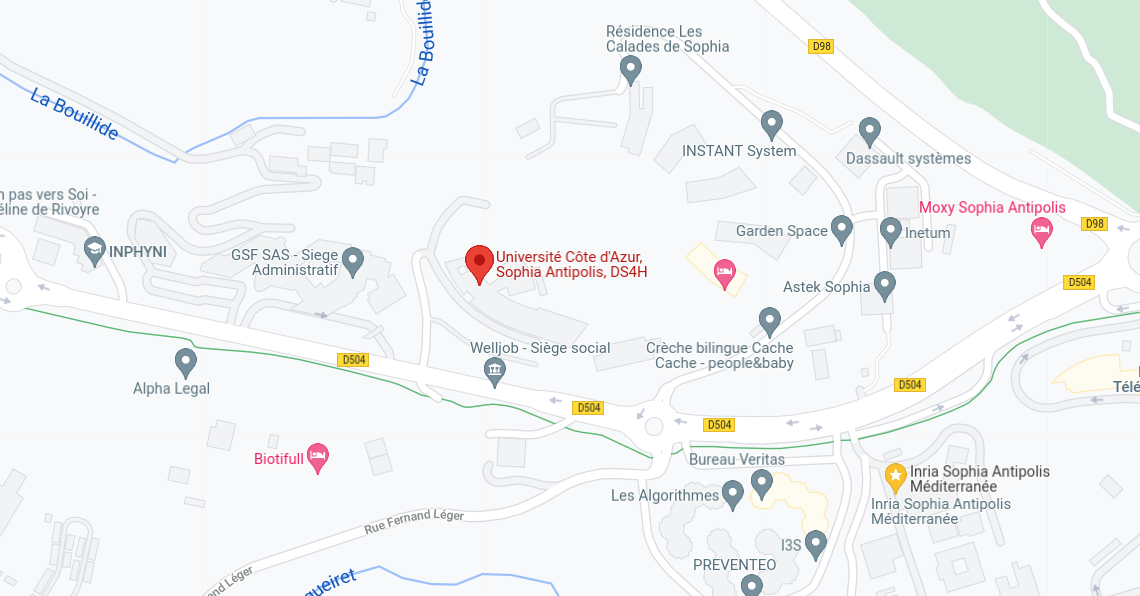
Classes will take place at Sophia Antipolis, M2 room, Campus des Lucioles, 1645 route des Lucioles, Biot 06410.

Validation

This course is validated with data science projects. Instructions can be found there.