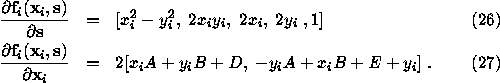Let us choose the normalization with A+C=1 (see Sect.4.1). The state vector can now be defined as:
The measurement vector is: 
.
As the conic parameters are the same for all points, we have the following
simple system equation:
and the noise term 
is zero. The observation function is
In order to apply the extended Kalman filter, we need to compute the
derivative of 
with respect to 
and that with respect to 
, which are given by
