The Iterated Extended Kalman Filter (IEKF) could be applied either globally or locally.
The global IEKF is applied to the whole observed data.
Given a set of n observations 
. The
initial state estimate is 
with covariance matrix
. After applying the EKF to the set 
, we get an estimate 
with covariance matrix
(the superscript, 1 here, denotes the number of iteration).
Before performing the next iteration, we must back propagate to time 
, denoted by 
. At iteration 2,
is used as the initial state estimate, but the
original initial covariance matrix is again used
as the initial covariance matrix at this iteration. This is because if
we use the new covariance matrix, it would mean we have two identical
sets of measurements. Due to the requirement of the back propagation
of the state estimate, the application of the global IEKF is very
limited. Maybe it is interesting only when the state does not evolve
over time [1]. In that case, no back propagation is required.
In the problem of estimating 3D motion between two frames, the EKF is
applied spatially, i.e., it is applied to a number of matches.
The 3D motion (the state) does not change from one match to another,
thus the global IEKF can be applied.
The local IEKF [8, 15] is applied to a single sample data by
redefining the nominal trajectory and relinearizing the measurement equation.
It is capable of providing better
performance than the basic EKF, especially in the case of significant
nonlinearity in the measurement function 
. This is because when 
is generated after
measurement incorporation, this value can serve as a better state
estimate than 
for evaluating 
and
in the measurement update relations. Then the state estimate
after measurement incorporation could be recomputed, iteratively if
desired. Thus, in IEKF, the measurement update relations are replaced
by setting 
(here, the
superscript denotes again the number of iteration) and doing iteration
on
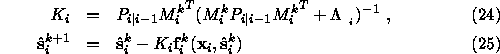
for iteration number 
and then setting 
. The iteration could be stopped when
consecutive values 
and 
differ
by less than a preselected threshold. The covariance matrix is then
updated based on 
.