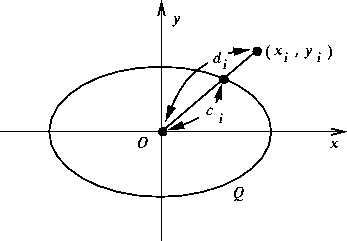
Figure 1: Normalized conic
The big advantage of use of algebraic distances is the gain in computational efficiency, because closed-form solutions can usually be obtained. In general, however, the results are not satisfactory. There are at least two major reasons.
To understand the second point, consider a conic in the normalized system (see fig:normal_conic):
![]()
The algebraic distance of a point ![]() to the conic Q is given by [3]:
to the conic Q is given by [3]:
![]()
where ![]() is the distance from the point
is the distance from the point ![]() to the center O of
the conic, and
to the center O of
the conic, and ![]() is the distance from the conic to its center along the
ray from the center to the point
is the distance from the conic to its center along the
ray from the center to the point ![]() . It is thus clear that a point at
the high curvature sections contributes less to the conic fitting than a point
having the same amount of noise but at the low curvature sections. This is
because a point at the high curvature sections has a large
. It is thus clear that a point at
the high curvature sections contributes less to the conic fitting than a point
having the same amount of noise but at the low curvature sections. This is
because a point at the high curvature sections has a large ![]() and its
and its
![]() is small, while a point at the low curvature sections has a
small
is small, while a point at the low curvature sections has a
small ![]() and its
and its ![]() is higher with respect to the same amount
of noise in the data points. Concretely, methods based on algebraic distances
tend to fit better a conic to the points at low curvature sections than to
those at high curvature sections. This problem is usually termed as high
curvature bias.
is higher with respect to the same amount
of noise in the data points. Concretely, methods based on algebraic distances
tend to fit better a conic to the points at low curvature sections than to
those at high curvature sections. This problem is usually termed as high
curvature bias.