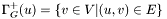 is the set of successors of
is the set of successors of 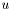 in the graph
in the graph 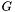 ;
;
Sid Touati. Register Saturation in Instruction Level Parallelism. International Journal of Parallel Programming, Springer-Verlag, Volume 33, Issue 4, August 2005. 57 pages.
Vincent Bouchitté was member of the LIP laboratory at Ecole Normale Supérieure de Lyon. He died after a long disease. He was 47 years old. Very discrete, he was very appreciated by all his colleagues and students. He leaves major results in graph theory and advised beautiful Ph.D. theses. He was buried at Salindre in France, his birthplace, on March 15th, 2005.
In memory of him, I implemented Dilworth decomposition. Vincent Bouchitté taught us beautiful algorithms and formal proofs on the subject.
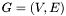 , the following notations were used by Vincent Bouchitté and are usually used in lattices and orders algebra:
, the following notations were used by Vincent Bouchitté and are usually used in lattices and orders algebra:
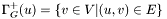 is the set of successors of
is the set of successors of 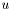 in the graph
in the graph 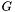 ;
;
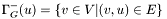 is the set of predecessors of
is the set of predecessors of 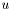 in the graph
in the graph 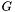 ;
;
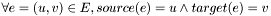 .
. 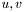 are called endpoints ;
are called endpoints ;
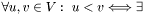 a path
a path 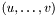 in
in  ;
;
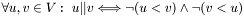 .
. 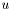 and
and 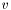 are said to be parallel ;
are said to be parallel ;
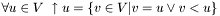 is the set of
is the set of 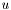 's ascendants including
's ascendants including 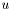 . In other terms, a node
. In other terms, a node 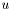 is an ascendant of a node
is an ascendant of a node 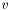 iff
iff 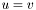 or if there exists a path from
or if there exists a path from 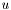 to
to 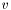 ;
;
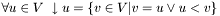 is the set of
is the set of 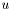 's descendants including
's descendants including 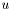 . In other terms, a node
. In other terms, a node 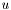 is a descendant of a node
is a descendant of a node 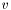 iff
iff 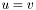 or if there exists a path from
or if there exists a path from 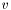 to
to 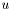 ;
;
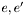 are adjacent iff they share an endpoint;
are adjacent iff they share an endpoint;
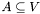 is an antichain iff all nodes belonging to
is an antichain iff all nodes belonging to 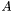 are parallel. Formally,
are parallel. Formally, 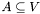 is an antichain in
is an antichain in 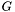 iff
iff 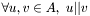 ;
;
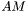 is a maximal antichain iff its size in terms of number of nodes is maximal. Formally,
is a maximal antichain iff its size in terms of number of nodes is maximal. Formally, 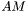 is a maximal antichain
is a maximal antichain 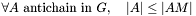 ;
;
 .
.
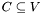 is a chain iff all nodes belonging to
is a chain iff all nodes belonging to 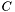 are not parallel. Simply, all nodes of a chain belongs to the same path in the DAG. Formally,
are not parallel. Simply, all nodes of a chain belongs to the same path in the DAG. Formally, 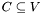 is a chain in
is a chain in 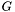 iff
iff 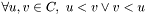 ;
;
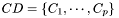 is a chain partition of
is a chain partition of 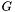 if any
if any 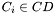 is a chain and:
is a chain and: ![$ \forall u \in V, \exists !i \in [1,p]: u \in C_i $](form_30.png) .
.
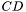 is minimal if its indice
is minimal if its indice 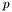 is minimal. Such minimal indice is noted
is minimal. Such minimal indice is noted 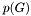 .
.
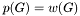 , and each maximal antichain is equivalent to a minimal chain decomposition (and vice-versa).
, and each maximal antichain is equivalent to a minimal chain decomposition (and vice-versa).int main(int argc, char *argv[]) { graph G; LEDA::string filename; set<node> MA; //maximal antichain node_array<int> C; //indices of chains node_list nl; h_array<int,node_list*> chain(nil); int i,status; int size_ma, // size of a maximal antichain size_mc; // size of a minimal chain decomposition node u; if(argc!=2){ cerr << argv[0] << ": Dilworth decomposition." << endl; cerr << "Usage:"<<argv[0] << " graph_filename" << endl; cerr << "The filename extension should be .gw for a graph in leda/gw format, or in .gml for a graph in GML format."<< endl; return EXIT_FAILURE; } filename=LEDA::string(argv[1]); if (filename.contains(LEDA::string(".gw"))) { cout<<"Reading GW" <<filename<<endl; status=G.read(filename); } else if (filename.contains(LEDA::string(".gml"))) { cout<<"Reading GML "<< filename<<endl; status=G.read_gml(filename); } else { cerr << "Usage:"<<argv[0] << " graph_filename" << endl; cerr << "The filename extension should be .gw for a graph in leda/gw format, or in .gml for a graph in GML format."<< endl; return EXIT_FAILURE; } switch(status){ case 0: case 2: break; case 1: cerr<< filename << " does not exist."<<endl; break; case 3: cerr<<filename <<" does not contain a graph"<<endl; break; default: return EXIT_FAILURE; } size_mc=MINIMAL_CHAIN(G, C); cout<<"Minimal Chain Decomposition"<<endl; cout<<"---------------------------"<<endl; cout<<"There are "<<size_mc<<" chains"<<endl; forall_nodes(u,G){ if ((chain[C[u]])==nil){ chain[C[u]]=new node_list; } (chain[C[u]])->append(u); } for(i=0;i<size_mc;i++){ cout<<"chain "<<i<<": "; forall(u, *chain[i]){ G.print_node(u); } cout<<endl; } size_ma=MAXIMAL_ANTI_CHAIN(G, MA); cout<<"Maximal Antichain"<<endl; cout<<"---------------------------"<<endl; cout<<"Size of this maximal anctichain : "<<size_ma<<" nodes"<<endl; cout<<"Here are all these nodes:"<<endl; i=0; forall(u, MA){ cout<<"node "<<i<<": "; G.print_node(u); cout<<endl; i++; } return EXIT_SUCCESS; }
