8 Améliorer le fonctionnement du CDPR, partie 1

Pour le moment le fonctionnement de notre système repose essentiellement sur la mesure de la rotation du tambour par un codeur. Nous avons vu que cela induit des problèmes majeurs:

• la dérive au cours du temps de la mesure, en particulier pour les treuils simples alors que nous l'utilisons pour déterminer la position de $B$
• la nécessité de procéder au démarrage à une calibration manuelle du CDPR
• pour les CDPR à 4 câbles l'impossibilité de repérer les câbles non tendus alors que la calcul de la position de $B$ le nécessite

Dans cette première partie nous allons proposer quelques améliorations, simples à mettre en oeuvre, de l'analyse et du dispositif matériel qui permettent d'améliorer les performances du CDPR.

8.1 Modèle d'enroulement

Pour les treuils simples nous n'avons pour le moment pas détaillé le mécanisme d'enroulement du câble sur le tambour. Selon la dimension du tambour on peut déterminer le nombre de spires jointives que l'on peut enrouler sur une couche. Pour la première couche une formule simple permet de déterminer à partir du rayon du tambour et du câble la longueur d'une spire et par conséquence la longueur totale du câble du tambour enroulé sur la couche. On peut répéter le processus pour les couches suivantes en prenant soin de considérer que le rayon d'enroulement augmente du diamètre du câble à chaque nouvelle couche. Si l'on a mesuré la longueur totale du câble on peut donc calculer pour chaque couche quel sera la distance minimum et maximum entre $A$ et $B$ mais aussi quel sera le rayon d'enroulement. La calibration initiale fournit la distance entre $A$ et $B$ ce qui permet de repérer sur quelle couche se trouve le câble donc le rayon d'enroulement courant. Lors du mouvement d'un tambour on va donc pouvoir déterminer de combien varie la longueur du câble selon le changement d'information du codeur et en prenant en compte les variations de rayon du tambour. Le suivi de cette longueur permet aussi de déterminer les moments où le câble change de couche ce qui permet la mise à jour du rayon d'enroulement. Ce modèle d'enroulement du câble permet de mieux prendre en compte les couches et donc améliore l'estimation des longueurs des câbles à partir des informations codeur. Toutefois il repose sur l'hypothèse d'un enroulement parfait du câble sur le tambour.

:

La longueur d'une spire d'une hélice de pas $p$ sur un cylindre de rayon $r$ est $\sqrt{(2\pi r)^2+h^2}$. Pour $n$ spires on a donc une longueur de $n\sqrt{(2\pi r)^2+h^2}$. Lorsque l'on passe passe à la couche suivante le rayon devient $r+d$ où $d$ est le diamètre du câble. Pour la $m$ème ouche la longueur totale du câble enroulé sur le tambour sera donc $\sum_{k=1}^{k=m} n\sqrt{(2\pi r+(k-1)d)^2+h^2}$

8.2 Un système de marques

Dans cette section on propose un ajour matériel très simple mais qui va permettre à la fois de réaliser la calibration de manière automatique mais aussi d'améliorer l'estimation des longueurs de câble. Pour la calibration nous avons vu qu'il est nécessaire d'avoir la longueur de chaque câble au démarrage du système ou avant son utilisation. Peut t'on concevoir un système qui pourrait automatiquement déterminer à un moment donné la longueur du câble et nous fournirait donc cette information ?

Pour cela on va modifier légèrement le matériel du CDPR, en supposant que câble est synthétique:

• on va coller sur le câble une marque c'est-à-dire un mince ruban d'un matériel conducteur d'électricité. Le plus simple pour cela est d'utiliser un ruban d'aluminium autocollant d'environ 1 cm de largeur et 2 cm de longueur que l'on enroule autour du câble. Cette marque va être placée sur le câble à une distance connue du point $B$,
• au niveau de l'oeil du point $A$ le câble va passer entre deux rouleaux que l'on va aussi recouvrir avec le même ruban d'aluminium L'un de ces rouleaux est connecté au pôle + de l'alimentation électrique et l'autre à un dispositif qui permet à un ordinateur de détecter un contact électrique

Une autre possibilité est de placer une marque de couleur sur le câble, d'une couleur très différente de celle du câble, et de placer en $A$ un dispositif optique de reconnaissance des couleurs (de tel dispositif sont disponibles et coûtent quelques euros). Ce dispositif enverra à l'ordinateur un signal indiquant la couleur de la marque lorsqu'elle passe en $A$.

Avec ce dispositif l'ordinateur va être capable de détecter quand la marque passe au point $A$ puisque le ruban sur le câble crée à ce moment un contact électrique (ou un changement de couleur). En pratique avant le montage du câble on place manuellement la marque à une distance connue de l'extrémité du câble. Au démarrage du système on s'arrange pour que chaque marque soit après le point $A$ de chaque câble. On enroule alors les câbles jusqu'à ce que l'ordinateur détecte le passage du câble au point $A$, auquel cas il arrête le déroulement. Lorsque tous les câbles sont arrêtés on sait quelle est la longueur de chaque câble: le système est calibré.

Mais la marque peut encore servir après la calibration. Lors du mouvement du CDPR il peut arriver qu'elle passe à nouveau au point $A$. A chacun de ces évènement on peut donc mettre à jour la longueur estimée du câble et ainsi corriger la dérive de cette estimation due au caractère aléatoire de l'enroulement sur le tambour. Mais on peut encore améliorer le système en plaçant sur chacun des câbles une deuxième marque entre la marque de calibration et le point $B$, à une distance connue de $B$. Pour le système à ruban conducteur on choisira cette distance pour qu'elle diffère sensible de celle de la marque de calibration. Pour le système à couleur la couleur de cette marque sera choisie différente de celle de la marque de calibration. Lors du passage d'une marque en $A$ si l'on sait dire quelle marque est détectée alors on connaît la longueur courante du câble. Avec le dispositif à couleur reconnaître la marque est trivial. Pour le dispositif à marque métallique on dispose à tout moment de l'estimation de longueur du câble, un peu différente de la longueur réelle mais qui en reste proche: lors d'une détection de marque on identifiera la marque en choisissant celle dont la distance au point $B$ est la plus proche de l'estimation.

Bien entendu rien n'empêche de placer sur le câble plus de deux marques. Pour le système à couleur le nombre de couleur détectable est limité mais on peut parfaitement se limiter à 3 couleurs possibles pour les marques: rouge, vert, bleu. La marque sera reconnue d'abord par sa couleur puis pour les marques de cette couleur on choisira celle dont la distance à $B$ est la plus proche de la longueur estimée. On fera de même pour les marques à ruban conducteur. Avec ce type de dispositif on obtient alors un système qui périodiquement remet à jour l'estimation des longueurs des câbles et limite donc considérablement la dérive de cette estimation. Il conviendra cependant de vérifier périodiquement l'état des marques et les renouveler si nécessaire.

Peut t'on relâcher la contrainte de la calibration qui consiste à démarrer d'une position où l'on connaît le sens à donner à la rotation du tambour pour que la marque de calibration soit détectée ? On va traiter séparément les cas où les marques sont électriques et celui où les marques sont de couleur.

Pour les marques électriques supposons que l'on a placé au moins 3 marques, les distances entre marques successives étant significativement différentes. Par exemple pour un câble dont la longueur entre $A$ et $B$ est au maximum de 10 mètres on va placer une marque à 6 mètres de $B$, la suivante à 5 mètres et la troisième à 3.5 mètres. Ces marques sont numérotées de 1 à 3. La calibration se fait câble par câble en enroulant le câble. A un moment une marque est détectée mais on ne sait pas dire quel est le numéro de cette marque. On continue l'enroulement jusqu'à la détection d'une nouvelle marque. On a mesuré la rotation du tambour entre les deux détections et en prenant un rayon moyen pour le tambour on a une estimation de la distance entre les deux marques détectées dont la valeur exacte est 1 mètre (marque 1 et 2 détectées) où 1.5 mètre (marque 2 et 3 détectée). En comparant l'estimation et les 2 possibilités de distance on peut déterminer le numéro de la dernière marque et donc calibrer le câble.

Un processus un peu plus complexe peut être utilisé si l'on a plus de 3 marques avec un nombre limité de distances possibles entre les marques (par exemple 1.5, 1, 0.5 mètres). Après la détection des deux premières marques on estime leur distance d'après la rotation du tambour, disons 1.2 mètres. On regarde alors dans la liste des distances entre marques toutes les paires dont la distance est égale à 1 mètres. Il peut y en avoir plusieurs donc on continue l'enroulement jusqu'à la détection d'une nouvelle marque, la distance de celle-ci à la marque précédente étant estimée par exemple a 0.6 mètres. On regarde alors les triplets de marques dont la distance entre la première et la seconde est de 1 mètres et la distance entre la deuxième et la troisième de 0.5 mètres. On continue les processus jusqu'à ce qu'il n'y ait plus qu'une possibilité ce qui nous dit quel est le numéro de la dernière marque détectée. On peut montrer qu'en général la détection de 3 marques suffit à calibrer le câble.

Considérons maintenant le cas des marques de couleur en supposant qu'on utilise 3 couleurs pour les marques: rouge (R), vert (V), bleu (B). L"astuce ici va être placer les marques de façon à ce si l'on regarde la séquence de couleurs de 3 marques qui se suivent alors il n'existe qu'un endroit sur le câble où l'on va trouver une séquence donnée. Par exemple considérons que les couleurs des marques sur les câbles est

$$RVBRVRRVVRBVVVBVBBRBRRRBBBVRV$$

La séquence RVB n'existe qu'au début du câble et nul part ailleurs. C'est aussi le cas de la séquence VRV qui se trouve à la fin du câble. Dans cet exemple on a placé 29 marques sur le câble et on peut montrer que ce nombre est le maximum que l'on peut avoir avec des séquences uniques et 3 couleurs détectables. Pour la calibration on enroule le câble jusqu'à ce que l'on ait détecté 3 marques. L'examen de leurs couleurs permet d'identifier la séquence et donc le numéro de la dernière marque détectée. Avec 29 marques et après calibration on recevra très régulièrement une information sur la la longueur réelle du câble et il y aura donc une dérive très faible de l'estimation de la longueur des câbles

: La construction de séquences de taille$n$ donnée toute différente avec un alphabet contenant $k$ symbole est bien connue en mathématique combinatoire: il s'agit des séquences de De Bruijn.

On peut même aller plus loin pour améliorer la fréquence avec laquelle on obtient une information exacte sur la longueur du câble. Pour cela on va placer non pas une station de détection sur le mât mais plusieurs, ce qui est montré sur la figure 17 dans le cas des marques de couleur. Les stations de détection sont les boîtes placées sur le mât.

Figure 17: Des marques de couleur sur le câble et plusieurs stations de détection du passage des marques dans le mât.

Pourquoi cette disposition est t'elle intéressante ? Prenons un câble avec 20 marques et supposons qu'il y a une station de détection des marques. Partant du câble totalement déroulé et enroulons le: il va y avoir 20 détections de marque. Si l'on a maintenant 3 stations de détection: pour le même processus on aura 60 détections de marques. Si aucune des détections n'est simultanées on aura donc, pour une même quantité de câble enroulé, beaucoup plus d'événements qu'avec une seule station. En conséquence la quantité de câble enroulée entre 2 détections va être beaucoup plus petite qu'avec une seule station. On peut montrer par exemple qu'avec un câble de 50 mètres, 29 marques et 3 stations la variation de longueur entre deux détections est généralement de 40 cm.

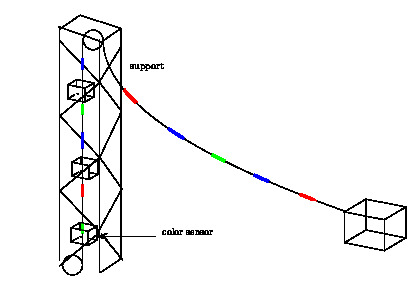
Entre deux détections on utilise l'estimation de la longueur reposant sur la mesure de la rotation du tambour, qui va être même améliorée: lors de deux détections successives on a à la fois la variation de longueur du câble et la rotation du tambour ce qui va fournir une estimée du rayon moyen réel du tambour, ce qui peut réduire les effets d'un enroulement un peu erratique. Un tel dispositif, facile à mettre en oeuvre, permet une amélioration significative de l'estimation des longueurs des câbles et donc de la précision du CDPR.

Comme indiqué il faut cependant veiller à ce que la détection des marques ne soit pas simultanée. Par exemple une mauvaise disposition des stations est de les mettre à une distance identique l'une de l'autre et de choisir cette même distance comme distance entre les marques. En effet avec cette disposition 3 marques arrivent simultanément sur les 3 stations, ce qui revient à n'avoir qu'un événement au lieu de 3.

La vidéo suivante montre ce qui se passe avec une ou trois stations de détection pour le même marquage du câble et la même quantité de câble enroulée. Les cercles en bas de la figure, représentent les détections des stations: ils sont incolores si la station ne détecte aucune couleur et changent de couleur lorsqu'une marque de cette couleur est détectée. Le nombre de détection de chaque station ainsi que le nombre total de détection sont indiqués. On voit qu'au prix d'un petit effort matériel d'augmentation du nombre de stations, le nombre de détection augmente considérablement pour un enroulement donné.

VIDEO

Le principe que nous avons décrit est similaire à celui du vernier qui est utilisé pour améliorer la précision de la mesure des longueurs avec un pied à coulisse. Nous avons utilisé ce dispositif pour notre prototype de CDPR MARIONET-ASSIST.