The CLEM project

Introduction

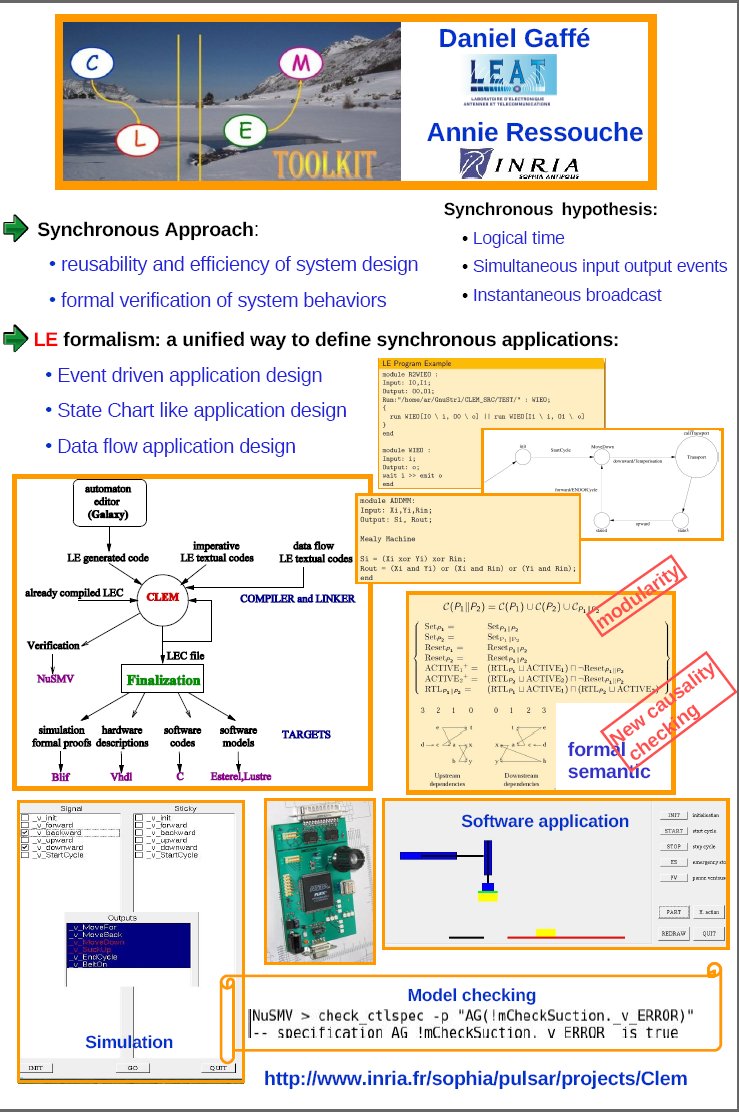
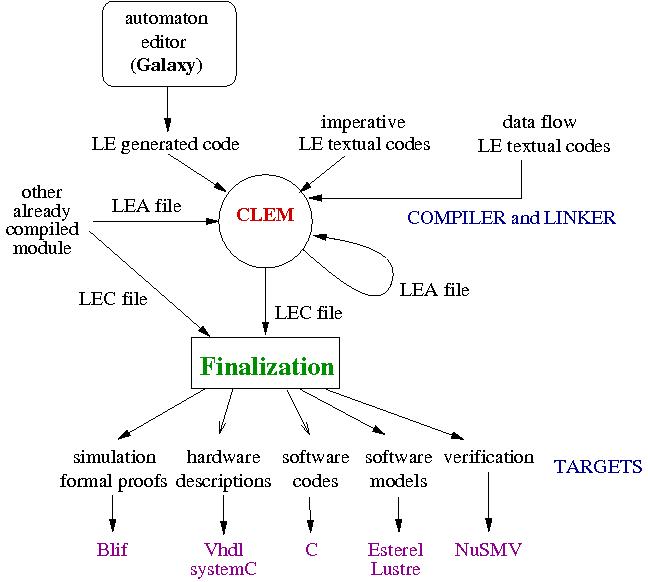
In collaboration with the LEAT team , we designed a compilation workflow around a synchronous language le. We supply a modular way to compile le and we develop the Clem toolkit around the language to design, simulate, verify and generate code for programs.

le language agrees with Model Driven Software Developement philosophy which is now well known as a way to manage complexity, to achieve high re-use level, and to significantly reduce the development effort. Therefore, we benefit from a formal framework well suited to compilation and formal validation. In practice, we defined two semantics for le: a behavioral semantics to define a program by the set of its behaviors, avoiding ambiguities in program interpretations; an equational semantics to allow modular compilation of programs into software and hardware targets (C code, VHDL code, SystemC code, FPGA synthesis, observers...). Our approach fulfills two main requirements of critical realistic applications: modular compilation to deal with large systems and model-based approach to perform formal validation.

Presentation

le Compilation

The main originality of this work is to be able to manage both modularity and causality. Indeed, only few approaches consider a modular compilation because there is a deep incompatibility between \textit{causality} and modularity. Causality means that for each event generated in a reaction, there is a causal chain of events leading to this generation. No causal loop may occur. Program causality is a well-known problem with synchronous languages, and therefore, it needs to be checked carefully. Thus, relying on semantics to compile a language ensures a modular approach but requires to complete the compilation process with a global causality checking. To tackle this problem, we introduced a new way to check causality from already checked sub programs and the modular approach we infer.

The equational semantics compute a Boolean equation system and we ensure both modularity and causality in computing all the partial orders valid for a system and we define a way to merge two partial orders. The algorithm which computes partial orders rely on the computation of two dependency graphs: the upstream (downstream) dependency graph computes the dependencies of each variable of the system starting from the input (output) variables. This way of compiling is the corner stone of our approach. We have three different algorithms to compute the partial orders valid for an equation system:

1. apply PERT method : inputs (resp. outputs) have date 0 and recursively increase of dates for each vertice in the upstream (resp downstream) dependencies graph;
2. apply graph theory:
   • compute the adjency matrix &Delta of upstream (resp. downstream) dependencies graph;
   • the length of the maximal path from a variable v to system inputs is characterized by the maximal k such that &Delta^k[v,i] &ne 0 for all inputs i.
3. apply fix point theory: the vector of earliest (resp. lastest) dates can be computed as the least fix point of a momotonic increasing function.

To be modular, we define a technique to compose two already sorted equation systems : first, we memorize the two dependency graphs of equation systems. Second, we define two merge algorithms relying on two different techniques:

1. propagation of common variables dates adjustement;
2. fix point characterisation starting with the vectors of already computed dates and considering only the variables in the dependencies (upstream and downstream) of common variables

The fix point characterization helps us to prove that the merge algorithm is correct (i.e we get the same partial orders using the merge algorithm on two previously sorted equation systems or when sorting the union of the two equation systems considered).

The Workflow

Relying on this approach, we designed a complete toolkit to specify, simulate and generate code for le programs:

Documentation

Clem Website

The website to get full documentation and downloads: Clem

Some Presentations

	Slides of the presentation at the Software Engineering Research, Management and Applications Conference (SERA 2008)
	Slides of the presentation at the Synchronous workshop (SYNCHRON 2010)

Poster

Here is a poster (presented at ASE 2008) which sums up the Clem workflow: