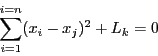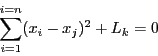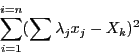Next: Implementation
Up: Solving systems of distance
Previous: Solving systems of distance
Contents
We consider here a special occurrence of quadratic equations that
describe distances between points in an  dimensional space.
Each equation
dimensional space.
Each equation 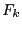 in such system may be written as:
in such system may be written as:
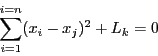
where 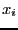 are unknowns (representing coordinates
of points) and
are unknowns (representing coordinates
of points) and 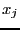 may be unknowns of constants.
A special occurrence of unknowns are the virtual points: the
coordinates
of these points are linear combination of the coordinates of the
points that are defined as the unknowns of the system. To illustrate
the concept of virtual points consider 5 fixed points on a rigid body in the
3-dimensional space. The coordinates of any of this point may be
expressed as a linear combination of the coordinates of the 4 other
points (as soon as these point are not coplanar). The concept of
virtual points has been introduced to allow a decrease in the number
of unknowns but also because without them distance equations will be
redundant and consequently the jacobian of the system of equations
will be singular at a solution thereby prohibiting us of using the
tests (such as Moore or Kantorovitch) that allows to determine that
there is one unique solution in a
given box.
may be unknowns of constants.
A special occurrence of unknowns are the virtual points: the
coordinates
of these points are linear combination of the coordinates of the
points that are defined as the unknowns of the system. To illustrate
the concept of virtual points consider 5 fixed points on a rigid body in the
3-dimensional space. The coordinates of any of this point may be
expressed as a linear combination of the coordinates of the 4 other
points (as soon as these point are not coplanar). The concept of
virtual points has been introduced to allow a decrease in the number
of unknowns but also because without them distance equations will be
redundant and consequently the jacobian of the system of equations
will be singular at a solution thereby prohibiting us of using the
tests (such as Moore or Kantorovitch) that allows to determine that
there is one unique solution in a
given box.
Equations involving
virtual points may be written as:
where the 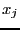 are unknowns and the
are unknowns and the 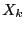 unknowns or constants.
Clearly system involving distance equations are of great practical
interest and ALIAS offers a specific algorithm to deal with such
type of systems.
unknowns or constants.
Clearly system involving distance equations are of great practical
interest and ALIAS offers a specific algorithm to deal with such
type of systems.
The method proposed in ALIAS to solve this type of systems is
based on the general procedure using the gradient and hessian. A first
difference is that it is not necessary to provide the gradient and
hessian function as they are easily derived from the system of
equations. Note also that due to the particular structure of the
distance equations the interval evaluation leads to exact bounds.
Furthermore
the algorithm we propose uses a special version of Kantorovitch
theorem (i.e. a version that produces a larger ball with a unique
solution in it compared to the general version of the theorem),
an interval Newton method, a specific version of the simplex method
described in section 2.14 and a specific version of
the inflation method described in section 3.1.6 (i.e. a
method that allows to compute directly the radius of a ball around a
solution that will contain only this solution). In addition two
simplification rules are used:
- as each function is a sum of square term each of them involving
different unknowns we verify if the interval evaluation of the term
has a positive part (in the opposite case the current box
is discarded) and we may update the unknowns so that the negative part
of the term is reduced (this is basically an application of the
concept of 2B-consistency). Hence the procedures described in
section 2.17 should not be used for distance equations.
- based on the triangle equation: each subset of equations
describing the distances between a set of 3 points is detected and the
algorithm verify if the triangle equation is satisfied and, in some
cases may update the boxes.
The algorithm returns as solution either boxes that satisfy
Kantorovitch theorem and therefore are reduced to a point or boxes
such that the function evaluations include 0 and have a width
lower than a given threshold.




Next: Implementation
Up: Solving systems of distance
Previous: Solving systems of distance
Contents
Jean-Pierre Merlet
2012-12-20