Next: Return code
Up: Solving systems of distance
Previous: Principle
Contents
A system of 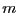 distance functions
has a specific description. First
consider distance function that involve only points of constant. Such
function may be written as:
distance functions
has a specific description. First
consider distance function that involve only points of constant. Such
function may be written as:
where the maximal number of square term is  and is described by a row of 2 matrices APOW, ACONS
and a vector LI. APOW is an integer matrix with
and is described by a row of 2 matrices APOW, ACONS
and a vector LI. APOW is an integer matrix with 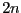 columns and
columns and 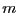 rows
that contain the unknown number
of each term in the function and in which a 0 means that the unknown
is a constant. The value of theses constants are given in the matrix
of real ACONS of size
rows
that contain the unknown number
of each term in the function and in which a 0 means that the unknown
is a constant. The value of theses constants are given in the matrix
of real ACONS of size 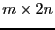 .
Finally the value of the constant
.
Finally the value of the constant 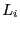 is
indicated in the vector LI of size
is
indicated in the vector LI of size 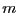 . For example consider a system
involving the 4 unknowns
. For example consider a system
involving the 4 unknowns
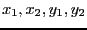 numbered from 1 to 4:
numbered from 1 to 4:
In that case APOW, ACONS, LI will be:
The two first elements of the first row of APOW (1, 0) describes the
first square term of the first equation and state that it is
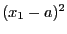 , the value of
, the value of 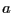 being given in the ACONS(1,2). Note that each square term must be written as
(unknown-unknown or constant
being given in the ACONS(1,2). Note that each square term must be written as
(unknown-unknown or constant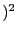 and not as (constant -unknown
and not as (constant -unknown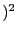 .
.
Consider now function involving virtual points. Each square term may
thus be written as:
where 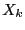 may be either a constant, an unknown or the coordinate of
a virtual point. Let
may be either a constant, an unknown or the coordinate of
a virtual point. Let 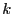 be the number of term of the form
be the number of term of the form
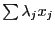 existing in the system.
Such equation is described by a matrix AVARV with
existing in the system.
Such equation is described by a matrix AVARV with 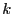 rows and a number of columns equal to the number of
unknowns. Each term
rows and a number of columns equal to the number of
unknowns. Each term
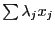 is numbered from 1 to k and
the row
is numbered from 1 to k and
the row 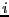 of AVARV will contain in position
of AVARV will contain in position 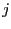 the value of
the value of
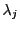 . The existence of the coordinate of
a virtual point in a
distance function will be indicated in APOW by a negative number
whose opposite is the number of the virtual coordinates.
Hence if we add to the previous system the third equation:
. The existence of the coordinate of
a virtual point in a
distance function will be indicated in APOW by a negative number
whose opposite is the number of the virtual coordinates.
Hence if we add to the previous system the third equation:
the third row of APOW will be (-1 0 -2 0), the third row of ACONS will be (0 3 0 1) and the third row of LI will be
-10. AVARV will have 2 row and 4 columns and is given as:
Among the 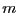 equations there will be
equations there will be 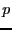 equations involving virtual
points. The system must be written in such way that first are defined
the
equations involving virtual
points. The system must be written in such way that first are defined
the 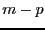 equations not involving virtual points and then the
equations not involving virtual points and then the 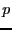 equations. Note also that in the current implementation
inequalities are handled although with less efficiency than
equations.
The algorithm is implemented as:
equations. Note also that in the current implementation
inequalities are handled although with less efficiency than
equations.
The algorithm is implemented as:
int Solve_Distance(int DimVar,int DimEq,
INTEGER_VECTOR &Type_Eq,
INTEGER_MATRIX &APOW,MATRIX &ACONS,VECTOR &LI,
int p,int k,MATRIX &AVARV,
INTERVAL_VECTOR & TheDomain,
int M,
double epsilonf,
int Stop,
INTERVAL_MATRIX & Solution,int Nb,
int (* Simp_Proc)(INTERVAL_VECTOR &))
The arguments are:
- DimVar: number of unknowns
- DimEq: number of equations and inequalities in the system
- Type_Eq: an integer array of dimension DimEq where
the j-th element indicates if the j-th function is an equation (value
=0), an inequality
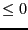 (value = -1) or an inequality
(value = -1) or an inequality 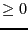 (value = 1)
(value = 1)
- p: number of functions involving virtual points
- k: number of virtual points
- TheDomain: box in which we are looking for
solution of the system
- M: the maximum number of boxes which may be
stored. In the algorithm we use the reverse storage mode except if the
global integer ALIAS_Parallel_Slave is set
to 1
(its default value is 0)
- epsilonf: either the maximal width of the function intervals for
a solution if it is not determined by using
Newton scheme or the accuracy used in the Newton scheme
- Stop: the possible values are 0,1,2
- 0: the algorithm will look for every solution in TheDomain
- 1: the algorithm will stop as soon as 1 solution has
been found
- 2: the algorithm will stop as soon as Nb solutions
have been found
- Solution: an interval matrix of size (Nb,m)
which will contained the solution intervals. This list is sorted using
the order specified by Order
- Nb: the maximal number of solution which will be returned
by the algorithm
- Simp_Proc: a user-supplied procedure that take as input
the current box and proceed to some further reduction of
the width of the box or even determine that there is no
solution for this box, in which case it should return
-1 (see note 2.3.3).
Remember also that you may use the 3B method to improve the efficiency of
this algorithm (see section 2.3.2).
The argument Simp_Proc in this procedure may be omitted.
The following variables play also a role in the computation:
- ALIAS_Diam_Max_Kraw: if the maximal width of the
ranges in a box is lower than this value, then the
Krawczyk operator will be used to determine if there is a unique
solution in the box (default value: 1.e10)
- ALIAS_Diam_Max_Newton: if the maximal width of the
ranges in a box is lower than this value, then the
interval Newton method will be used either to try to reduce
the width of the box or to to ensure that there is no solution of the
system in the box (default value: 1.e10)
- ALIAS_Permute_List: if the value of this flag is
 the
algorithm will permute the current list with the largest box in the
list of boxes to process (as the algorithm uses systematically the
Newton scheme with as initial guess the center of the current box
permutation may allow to find quickly new solutions)
the
algorithm will permute the current list with the largest box in the
list of boxes to process (as the algorithm uses systematically the
Newton scheme with as initial guess the center of the current box
permutation may allow to find quickly new solutions)
Subsections




Next: Return code
Up: Solving systems of distance
Previous: Principle
Contents
Jean-Pierre Merlet
2012-12-20