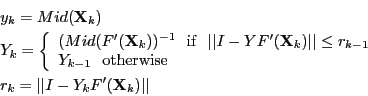Next: Implementation
Up: Krawczyk method for solving
Previous: Krawczyk method for solving
Contents
Let 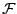 be a system of
be a system of 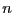 equations in the
equations in the 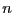 unknowns
unknowns 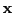 . Let
. Let 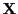 be a range vector for
be a range vector for 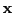 and
and
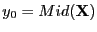 . Let
. Let 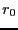 be the norm of the matrix
be the norm of the matrix
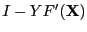 . Let
the following iterative scheme for
. Let
the following iterative scheme for 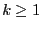 :
:
Let define 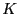 as:
as:
If
then the previous iterative scheme will converge to the unique
solution of 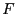 in
in 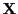 [8]. The procedure described in
section 3.1.1 enable to verify if the scheme will be
convergent.
[8]. The procedure described in
section 3.1.1 enable to verify if the scheme will be
convergent.
Jean-Pierre Merlet
2012-12-20
![]() be a system of
be a system of ![]() equations in the
equations in the ![]() unknowns
unknowns ![]() . Let
. Let ![]() be a range vector for
be a range vector for ![]() and
and
![]() . Let
. Let ![]() be the norm of the matrix
be the norm of the matrix
![]() . Let
the following iterative scheme for
. Let
the following iterative scheme for ![]() :
: