Implementation

The procedure for using Newton method is:

 
int Newton(int n,VECTOR (* TheFunction)(VECTOR &), 
        MATRIX (* Gradient)(VECTOR &),
        VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)

with

• n: number of equations
• TheFunction: a procedure which return the value of the equation for given values of the unknowns (see note 2.3.4.3)
• Gradient: a procedure which return the Jacobian matrix of the system for given values of the unknowns (see note 2.4.2.2)
• Input: at the start of the procedure the estimate of the solution, at the end of the procedure the solution
• Accuracy: the procedure return a solution if there is an Input such that 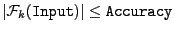$\vert{\cal F}_k({\tt Input})\vert \le {\tt Accuracy}$ for all 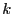$k$ in [1,$n$].
• MaxIter: the procedure will return a failure code if a solution is not found after MaxIter iteration
• Residu: the value of the equations for the solution

Note that it also possible to use in the Newton method the interval evaluation of the equation and of the Jacobian matrix which are necessary for the general purpose solving algorithm with Jacobian (see section 2.4). The syntax of this implementation is:

 
int Newton(int Dimension,
        INTERVAL_VECTOR (* IntervalFunction)(int,int,INTERVAL_VECTOR &), 
        INTERVAL_MATRIX (* IntervalGradient)(int, int, INTERVAL_VECTOR &),
        VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)

• IntervalFunction: a function which return the interval vector evaluation of the equations, see the note 2.3.4.3
• IntervalGradient: a function which the interval matrix of the jacobian of the equations, see the note 2.4.2.2

To avoid overflow problem it is possible to use the vector ALIAS_Newton_Max_Dim that must be resized to the number of unknowns and in which will be indicated the maximal possible value of each variable after each Newton operation. If one of these values is exceeded Newton will return 0.

The version of Newton method with constant 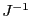$J^{-1}$ matrix is implemented as:

 
int Newton(int n,VECTOR (* TheFunction)(VECTOR &), 
        MATRIX &InvGrad,VECTOR &Input,double Accuracy,int MaxIter,VECTOR &Residu)

There is a special implementation of Newton method for univariate polynomial 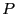$P$:

 
int Newton(int Degree,REAL *Input,VECTOR &Coeff,double Accuracy,int Max_Iter,REAL *Residu)

with:

• Degree: degree of the polynomial
• Input: on entry an estimate of the solution and on exit the solution
• Coeff: coefficient of the polynomial ordered in increasing degree
• Accuracy: Input is a solution if |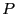$P$(Input|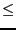$\le$ Accuracy
• MaxIter: the procedure will return a failure code if a solution is not found after MaxIter iteration
• Residu: the value of the polynomial for the solution

In that case we may have a problem if the Accuracy cannot be reached due to numerical errors. If you have determined that Newton should converge (using for example Kantorovitch theorem, see section 3.1.2) then you may use the procedure Newton_Safe with the same argument: this procedure will return the solution which has led to the lowest Residu during the Newton scheme.

An example of use of the Newton method is presented in section 15.1.1, where it is compared to alternative methods.