



Next: Implementation
Up: Newton method for solving
Previous: Newton method for solving
Contents
Let 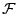 be a system of
be a system of  equations in the
equations in the  unknowns
unknowns 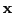 and
and 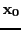 be an estimate of the solution of the system.
Let
be an estimate of the solution of the system.
Let 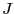 be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
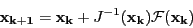 |
(2.6) |
starting with 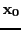 may converge toward a solution of the system.
may converge toward a solution of the system.
A simplified Newton method consist in using a constant matrix in
the classical Newton method, for example the inverse Jacobian matrix
at some point like 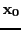 . The iterative scheme become:
. The iterative scheme become:
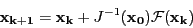 |
(2.7) |
Although the simplified method may need a larger number of iteration
before converging than the classical scheme each iteration has a lower
computation time as there is no computation of the
inverse of the Jacobian matrix. This method may also encounter
convergence
problem as it has a
convergence ball smaller than the classical Newton method.
Newton method has advantages and drawbacks that need to be known in
order to use it in the best way:
- it may really be fast: this may be important, for example in
real-time control
- it is very simple to use
- but it does not necessarily converge toward the solution
"closest" to the estimate (see the example in section 15.1.2)
- but it may not converge. Kantorovitch theorem
(see
section 3.1.2) enable to determine the size of the convergence
ball but this size is usually small (but quite often in practice the
size
is greater than the size given by the theorem which however is exact
in some cases)
- but a numerical implementation of Newton may overflow




Next: Implementation
Up: Newton method for solving
Previous: Newton method for solving
Contents
Jean-Pierre Merlet
2012-12-20
![]() be a system of
be a system of ![]() equations in the
equations in the ![]() unknowns
unknowns ![]() and
and ![]() be an estimate of the solution of the system.
Let
be an estimate of the solution of the system.
Let ![]() be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
be the Jacobian matrix of the system of equation. Then
the iterative scheme defined by:
![]() . The iterative scheme become:
. The iterative scheme become: