



Next: Implementation
Up: Interval Analysis
Previous: Interval Analysis
Contents
This section is freely inspired from the book [5].
An interval number is a real, closed interval
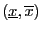 . Arithmetic
rules exist for interval numbers. For example let two interval numbers
. Arithmetic
rules exist for interval numbers. For example let two interval numbers
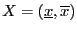 ,
,
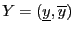 , then:
, then:
An interval function is an interval-valued function of one or
more interval arguments. An interval function 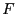 is said to be inclusion monotonic if
is said to be inclusion monotonic if
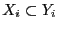 for
for 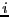 in
in ![$[1,n]$](img11.png) implies:
implies:
A fundamental theorem is that any rational interval function evaluated
with a fixed sequence of operations involving only addition,
subtraction, multiplication and division is inclusion monotonic.
This means in practice that the interval evaluation
of a function gives bounds (very often overestimated) for the value of
the function: for any specific values of the unknowns within their
range the value of the function for these values will be included in
the interval evaluation of the function. A very interesting point is
that the above statement will be true even taking into account
numerical errors. For example the number 1/3, which has no exact
representation in a computer, will be represented by an interval
(whose bounds are the highest floating point number less than 1/3 and
the smallest the lowest floating point number greater than 1/3) in
such way that the multiplication of this interval by 3 will include
the value 1. A straightforward consequence is that if the interval
evaluation of a function does not include 0, then there is no root of
the function within the ranges for the unknowns.
In all the following sections an interval for the variable 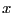 will be
denoted by
will be
denoted by
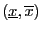 . The width or diameter of an interval
. The width or diameter of an interval
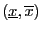 is the
positive difference
is the
positive difference
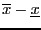 .
The mid-point of an interval is defined as
.
The mid-point of an interval is defined as
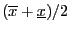 .
.
A box
is a set of intervals. The width of a box is the largest width of the
intervals in the set and the center of the box is the vector
constituted with the mid-point of all the intervals in the set.




Next: Implementation
Up: Interval Analysis
Previous: Interval Analysis
Contents
Jean-Pierre Merlet
2012-12-20
![\begin{eqnarray*}
&&X+Y= [\underline{x}+\underline{y},\overline{x}+\overline{y}]\\
&&X-Y= [\underline{x}-\overline{y},\overline{x}-\underline{y}]
\end{eqnarray*}](img7.png)
![\begin{eqnarray*}
&&X+Y= [\underline{x}+\underline{y},\overline{x}+\overline{y}]\\
&&X-Y= [\underline{x}-\overline{y},\overline{x}-\underline{y}]
\end{eqnarray*}](img7.png)
![]() will be
denoted by
will be
denoted by
![]() . The width or diameter of an interval
. The width or diameter of an interval
![]() is the
positive difference
is the
positive difference
![]() .
The mid-point of an interval is defined as
.
The mid-point of an interval is defined as
![]() .
.