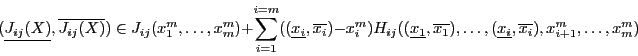Next: Single bisection mode
Up: General purpose solving algorithm
Previous: General purpose solving algorithm
Contents
In this new algorithm we will try to improve the evaluation of the
function intervals by using the Hessian of the functions. This
improvement is based on a sharper analysis of the monotonicity of the
functions which in turn is based on a sharper evaluation of the
Jacobian matrix of the system. The element 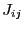 of the Jacobian matrix
at row
of the Jacobian matrix
at row 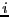 and column
and column 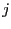 is:
is:
Now consider the corresponding line of the Hessian matrix which is:
The elements of this line indicate the monotonic behavior of the
elements of the Jacobian matrix. If some elements in this line have a
constant sign, then the elements of the Jacobian are monotonic with
respect to some of the unknowns and using this monotonicity we may
improve the evaluation of the element of the Jacobian
matrix. This improvement has to be
applied recursively: indeed as we will evaluate the Jacobian elements
for boxes in which some components have now a fixed
value the evaluation of the Hessian matrix for these boxes
may lead to a larger number of the component of the Hessian which have
a constant sign. The recursion will stop if all the component of the
Hessian line have a constant sign or if the number of component with a
constant sign does not increase.
Note also that not all the function must be differentiable to use this
procedure: only one of them is sufficient. In that case you will have
however to set special values in the gradient and hessian function
(see 2.4.2.2).
We will also use the Hessian in order to try to sharpen the evaluation
of 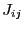 . Let the box intervals be
. Let the box intervals be
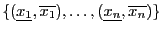 .
Let
.
Let 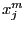 be the middle point of
be the middle point of
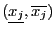 and
and
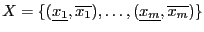 be the box. Then:
be the box. Then:
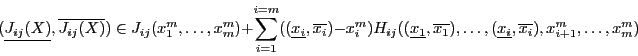 |
(2.5) |
see [5], pp. 52. This expression enable to get in some
cases a sharper bound on 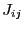 .
.
The improvement of the evaluation of the function intervals is due to
the fact that a sharper evaluation of the Jacobian matrix may lead to
a larger number of Jacobian elements with constant sign than with the
direct evaluation of the Jacobian matrix. To speed up the algorithm we
store the Jacobian matrix of each box: this enable to
avoid the evaluation of the components of the Jacobian matrix which
have a constant sign when bisecting the box
Another interest of the Hessian is that it enable to use Kantorovitch
theorem. This theorem (see section 3.1.2) can be applied if the
number of unknowns is equal to the number of equations and
enable to determine boxes in which there is an unique
solution, solution which can be found using Newton method (see
section 2.9) with as estimate of the solution any point
within the boxes.
We will use this theorem at three possible levels:
- level 0: we want solution intervals for which the maximal width is equal
or lower than a given threshold. In that case imagine that two
solution intervals have been found at some point of the algorithm,
this two solutions being close. We will apply Kantorovitch theorem for
the center of the two solution intervals. In the most favorable case
one of them will contain an unique solution while the boxes
given by Kantorovitch theorem will cover the other one: consequently
this input intervals will be eliminated of the solution
intervals. Therefore Kantorovitch theorem will eliminate spurious
solution intervals and we don't need to indicate a minimal distance
between the solution intervals.
- level 1: we look for solution intervals whose width has no importance as
soon as we are sure that they contain one unique solution which can be
found using Newton method with as estimate of the solution any point
within the solution intervals. In that case we will apply Kantorovitch
theorem for each boxes which appear during the algorithm. If
the theorem give a solution intervals we will store it in the solution
list and update the remaining boxes of the list so that none
of them contain the solution intervals. A consequence is that the
width of the solution intervals cannot be determined beforehand while
each solution intervals that have been determined using this method
contain one unique solution which can be determined using Newton
method.
- level 2: we apply Newton method for each box and if
Newton converge toward a solution within the current box we
store the box as solution interval. The boxes in the list are then
filtered so that none of them contains the solution interval.
Furthermore we use the inflation method presented in
section 3.1.6 to increase the width of the box in which we
may guarantee that there is a unique solution.
As for the method using only the gradient
we use the Hansen-Sengupta version of the interval
Newton method to improve the
boxes
(see [21]).
Subsections




Next: Single bisection mode
Up: General purpose solving algorithm
Previous: General purpose solving algorithm
Contents
Jean-Pierre Merlet
2012-12-20
![]() . Let the box intervals be
. Let the box intervals be
![]() .
Let
.
Let ![]() be the middle point of
be the middle point of
![]() and
and
![]() be the box. Then:
be the box. Then: