Let ![]() be the middle point of
be the middle point of
![]() and
and
![]() be the box. Then:
be the box. Then:
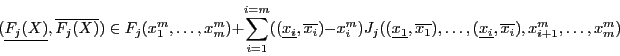 |
(2.4) |
This evaluation is embedded into the evaluation procedure of the solving algorithms using the Jacobian. It is also available in its general form as
INTERVAL_VECTOR Centered_Form(int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Center,
INTERVAL_VECTOR &Input)
where
INTERVAL Centered_Form(int k,int DimVar,int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
VECTOR &Center,
INTERVAL_VECTOR &Input)
which is used to evaluate only expression number
A more sophisticated evaluation for the centered form is based on
Baumann theorem [18]. First we define the procedure
cut(double x,INTERVAL X) as:
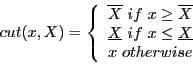
INTERVAL_VECTOR BiCentered_Form(int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
where
INTERVAL_VECTOR BiCentered_Form(int k,int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
Another variant is based on the property that the numerical interval evaluation of the product J(Input)(Input-Center) may be overestimated as there may be several occurence of the same variable in this product. We may assume that this product has been computed symbolically, then re-arranged to reduce the number of occurence of the same variable leading to a procedure in MakeF format that computes directly the product. The syntax of the bicentered form procedure is
INTERVAL_VECTOR BiCentered_Form(int DimVar,
int DimEq,
INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR (* ProdGradient)(int, int, INTERVAL_VECTOR &),
INTERVAL_VECTOR &Input,
int Exact)
where ProdGradient is the procedure that computes the product
J(Input)(Input-Center), being understood that the Center
is available in the global variable
ALIAS_Center_CenteredForm.