



Next: Implementation
Up: Lagrange-MacLaurin theorem
Previous: Lagrange-MacLaurin theorem
Contents
Let 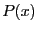 be an univariate polynomial of degree
be an univariate polynomial of degree  :
:
Assume 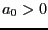 and let
and let 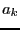 (
(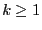 ) be the first negative
coefficients of
) be the first negative
coefficients of 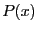 (if
(if 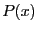 has no negative coefficients then
there is no positive real root).
has no negative coefficients then
there is no positive real root).
The upper bound 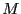 of the value of the positive real root is:
of the value of the positive real root is:
where 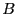 is the greatest absolute value of the negative coefficients
of
is the greatest absolute value of the negative coefficients
of 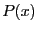 ,[3],[13].
,[3],[13].
If we define:
Then the upper bound of the positive real roots of 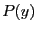 is the lower
bound
is the lower
bound 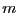 of the positive real root of
of the positive real root of 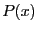 . Consequently if
. Consequently if 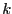 and
and 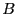 are computed for the polynomial
are computed for the polynomial 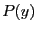 then
then
Jean-Pierre Merlet
2012-12-20
![]() of the value of the positive real root is:
of the value of the positive real root is:
![\begin{displaymath}
m=\frac{1}{1+\sqrt[n-k]{\frac{B}{a_n}}}
\end{displaymath}](img513.png)