



Next: Implementation
Up: Kantorovitch theorem
Previous: Kantorovitch theorem
Contents
Let a system of  equations in
equations in  unknowns:
unknowns:
each 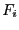 being at least
being at least 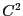 .
Let
.
Let 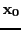 be a point and
be a point and
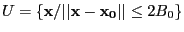 , the norm being
, the norm being
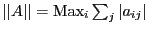 .
Assume that
.
Assume that 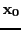 is such that:
is such that:
- the Jacobian matrix of the system has an inverse
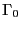 at
at 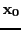 such that
such that
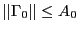
-
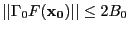
-
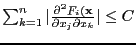 for
for
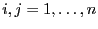 and
and 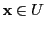
- the constants
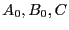 satisfy
satisfy
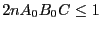
Then there is an unique solution of 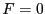 in
in 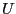 and Newton method
used with
and Newton method
used with 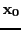 as estimate of the solution will converge toward
this solution [3].
An interesting use of Kantorovitch theorem can be found in
section 2.5.
as estimate of the solution will converge toward
this solution [3].
An interesting use of Kantorovitch theorem can be found in
section 2.5.
Jean-Pierre Merlet
2012-12-20