



Next: Implementation
Up: Moore theorem
Previous: Moore theorem
Contents
Let a system of 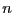 equations in
equations in 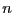 unknowns
unknowns
![$
F=\{ F_i(x_1,\ldots,x_n)=0, i\in [1,n]\}
$](img411.png) each
each 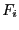 being at least
being at least 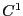 . Let
. Let 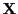 be a range vector for
be a range vector for
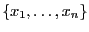 ,
, 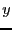 a point inside
a point inside 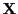 and
and 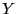 an
arbitrary nonsingular real matrix. Let define
an
arbitrary nonsingular real matrix. Let define 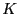 as:
as:
and let 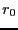 be the norm of the matrix
be the norm of the matrix
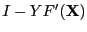 .
If
.
If
then there is a unique solution [16] of 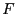 in
in 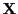 .
This unique solution can be found using Krawczyk solving method (see
section 2.10).
.
This unique solution can be found using Krawczyk solving method (see
section 2.10).
Jean-Pierre Merlet
2012-12-20