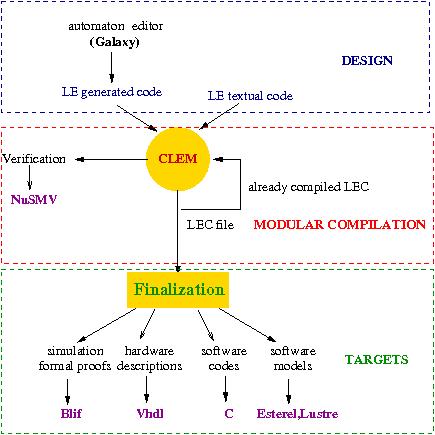
CLEM Workflow
- a design phase to describe applications;
- a compilation phase to compile programs into intermediate LEC code;
- a generation phase to produce a targeted output code.
Design of Applications
To design applications, users rely on the LE language. The language unit is a named module. The module interface declares the set of input events it reacts to and the set of output events it emits. In addition, the location of external already compiled sub modules is also specified in module interface. The module body is expressed using a set of operators. The language's operators and constructions are chosen to fit the description of reactive applications as a set of concurrent communicating sub-systems. Communication takes place between modules or between a module and its environment. Subsystems communicates via events. Besides, some operators (wait, pause) are specially devoted to deal with the logical time. The overall LE syntax is not detailed here. Nevertheless LE operators are summarized in the following table:
| emit speed | signal speed is immediately present in the environment |
| present S { P1} else { P2} | If signal S is present P1 is performed otherwise P2 |
| P1 >> P2 | perform P1 then P2 |
| P1 || P2 | synchronous parallel: start P1 and P2 simultaneously and stop when both have terminated |
| abort P when S | perform P until an instant in which S is present |
| loop {P} | perform P and restart when it terminates |
| local S {P} | encapsulation, the scope of S is restricted to P |
| run M | call of module M |
| pause | stop until the next reaction |
| wait S | stop until the next reaction in which S is present |
| A(M; T ; Cond;Mf ;O; &lambda) | automata specification |
| E(I;O;R;D) | equation system definition |
We just underline the presence of the run module operator that calls an external module and supports a renaming of the interface signals of the called module. It is through this operator usage that modular compilation is performed. Moreover, a graphical editor ( GALAXY ) to draw automata can be used as a front end and can generate LE textual language.
Modular Compilation
Compilation
The core of the toolkit is the (also called) CLEM compiler. It relies on the constructive equational semantic of LE language. The compiler straightly implements the semantic rules to compile each program into a &xi equation system. But to rely on equation systems to generate code, simulate or link with external code requires to find an evaluation order, valid for all synchronous instants. Usually, in the most popular synchronous languages existing, this order is static. This static order forbids any separated compilation mechanism as shown in this example.
To allow a separated compilation, independent signals must stay not related : we aim at building an incremental partial order. Hence, we keep enough information on signal causality to preserve the independence of signals, thanks to the &xi status attributed to each signal. At this aim, we define two integer variables for each equation, namely ( CanDate , MustDate) to record when the equation is evaluated. The CanDate characterizes the earliest date when the equation can be evaluated. The MustDate characterizes the latest date when the equation must be evaluated to respect the critical time path of the equation system. Dates are ranges in a discrete time scale and we call them levels. Level 0 characterizes the equations evaluated first because they depend of free variables, while level n+1 characterizes the equations that require the evaluation of variables from lower levels (from n to 0) to be evaluated. Equations of same level are independent and so can be evaluated whatever the chosen order is. Indeed, a couple of levels is associated with each equations. This methodology is inspired from the PERT method. This technique allows to deal with partial orders in equation systems and not immediately force the choice of a total arbitrary order. We detail our sorting algorithm here.
|
The approach we adopt allows to not choose a total order, but to keep all the available evaluation orders for each equation system. In order to be modular, we introduce a saving format (called the LEC format) that records the equation system of programs together with their variables evaluation dates. |
Modularity
The algorithm we present here allows to link two partial orders in an efficient way, avoiding to compute again the overall partial order. As a consequence, we can rely on such an approach to ensure separated compilation. Indeed, we only need to link a main module equation system with an already compiled sub module (called within a run instruction), and we perform this linking operation in just adjusting the dates of their common variables.
Verification
An attractive consequence of our approach is the ability to verify program behaviors. The correctness of a system with respect to an expected behavior is verified by checking whether a structure that models the system satisfies a formula describing that behavior. Such a formula is usually written by using a temporal logic. Most existing model checking techniques are based on a representation of the concurrent system by means of a Labeled Transition System (LTS). The equational semantic of LE language yields an equation system which encodes the set of program behaviors. Thus model checking techniques apply.. As a consequence, we can rely on model checking based tools to verify property of LE language. To this aim, we offer a translation of compiled LE program into smv format in order to feed the NuSMV model checker.
Practical Issues
We rely on the equational semantic to compile LE programs. To this aim we first associate a &xi equation system with the body of a program. Doing that, according to the constructive approach we trust in, we refine the value of signal and register status in the environment. Then, we translate each &xi equation system into a boolean equation system. This translation relies on a mapping that encodes each element of &xi algebra with a pair of boolean values. This encoding allows us to translate each &Xi equation system into a boolean equation system (each equation being encoded by two boolean equations).
In order to perform separate compilation of LE programs, we introduce the LEC internal compilation format. This format is highly inspired from the Berkeley Logic Interchange Format (BLIF). This latter is a very compact format to represent netlists and we just add to it syntactic means to record the CanDate and MustDate of each variable. Practically, CLEM compiler, among other output codes, generates LEC format in order to reuse already compiled code in an efficient way, thanks to the PERT method we implement.
Finalization
This approach to compile LE programs requires to be completed by what we call a finalization phase. This latter is specific to our approach because the separated compilation implies to keep the &perp status of signals during the compilation phase unlike the others synchronous approaches. A classical difficult problem in the compilation of synchronous languages is the "reaction to absence": signals are never set to absent and their final absent status is detected by a global propagation of signal status on the overall program. But these compilation algorithms prevent any separated compilation because they need a global vision of all status signals. In our approach, we keep the &perp status of signal until the end of compilation and we drive back the absence resolution at the end of the process and we call it finalization. Hence, we replace all &perp events by absent events. Notice that the finalization operation is harmless. The sorting algorithm relies on propagation of signal values, and the substitution of &perp by 0 cannot change the resulting sorted environment.
Then, finalized boolean equation system are translated in different targeted languages.
Simulation
To simulate LE programs, we translate the finalized boolean equation system into BLIF format and we feed a graphical simulation tool ( blif_simul). This simulation phase is illustrated in the example page.
Code Generation
To effectively run real applications, several output languages are provided in the CLEM toolkit:
- software models: lustre, esterel;
- hardware description : Vhdl;
- software code : C.
A lecto processor is provided within the CLEM toolkit to generate these output codes.
CLEM Usage
We design a graphical CLEM main panel.
A shell command can be used instead of the graphical CLEM panel:
clem [-debug] [-simul] [-lec] [-C dir][-o file] [-no_suppress_wires]
[-comp_files "[" lec file list"]" ] [-main mainname] filename