Définition 2.1 (Arc-consistance d'un domaine [
1])
Soit
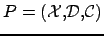
un
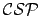
dont les domaines sont finis,
et
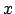
une variable de
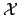
dont le domaine est
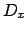
.
On dit que
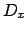
est arc-consistant ssi pour chaque contrainte
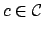
, toute valeur
de
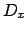
a un support dans les domaines des autres variables de
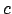
.
Exemple 2.1
Soit le
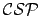
suivant :
Ce
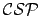
est arc-consistant mais n'a pas de solutions. On verra dans la section
2.2.1, comment la contrainte globale all-diff permet de résoudre ce problème.
![\includegraphics[scale=0.7]{consist.eps}](img90.png)