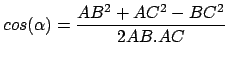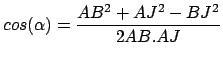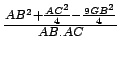


suivant: Démonstration de la propriété
monter: Bibliographie
précédent: Bibliographie
Table des matières
Soit 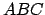 un triangle et
un triangle et 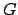 son centre de gravité.
son centre de gravité.
Soit 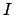 ,
, 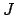 et
et 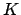 les milieux respectifs des segments
les milieux respectifs des segments ![$ [AB]$](img308.png) ,
, ![$ [AC]$](img309.png) et
et ![$ [BC]$](img310.png) .
Soient
.
Soient
![$ \alpha, \beta, \gamma \in [0, \pi]$](img311.png) , les angles non-orientés incidants respectivement aux sommets
, les angles non-orientés incidants respectivement aux sommets 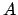 ,
, 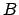 et
et 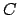 .
.
Figure:
Un triangle 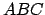 et son centre de gravité
et son centre de gravité 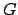
|
|
Deux propriétés du centre de gravité, que nous ne démontrerons pas, vont nous servir dans cette preuve :
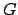 est l'intersection des médianes du triangle.
est l'intersection des médianes du triangle.
-
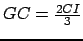 ,
,
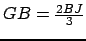 et
et
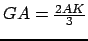 .
.
On peut calculer le cosinus de l'angle 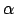 dans le triangle ABC en fonction
des distances
dans le triangle ABC en fonction
des distances 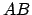 ,
, 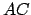 et
et 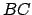 :
:
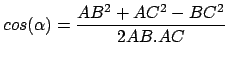 |
(1) |
De même, on peut calculer ce cosinus dans le triangles 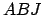 :
:
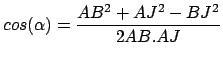 |
(2) |
Si 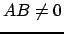 et
et 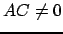 alors avec ces deux égalités on obtient :
alors avec ces deux égalités on obtient :
On peut obtenir les autres égalités en mettant en relation de la même façon les cosinus de 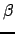 et
et 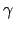 dans les triangles
dans les triangles 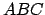 avec
avec 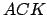 et
et 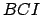 .
.  .
.
Ce qui est intéressant dans cette preuve est l'égalité des cosinus.
Cela veut dire que la position dans l'espace du barycentre est liée aux angles du triangle.
L'introduction de ce point va donc nous permettre de faire un meilleur filtrage,
puisqu'il met en jeu implicitement la notion d'angle.



suivant: Démonstration de la propriété
monter: Bibliographie
précédent: Bibliographie
Table des matières
Heikel Batnini
2002-10-22
![\includegraphics[scale=0.5]{abc.eps}](img312.png)