A formal-numerical approach to determine the presence of singularity within the workspace of a parallel robot

J-P. Merlet
INRIA Sophia-Antipolis
France

Abstract: Determining if there is a singularity within a given workspace of a parallel robot is an important step during the design process of this type of robot. As this singular configuration must be avoided the designer may be interested only in a straight yes/no answer.

We consider in this paper a Gough-type parallel robot and we present algorithms which enable to determine if there is any singularity within a 6D workspace expressed either in term of generalized coordinates (position/orientation of the platform) or articular coordinates (lengths of the legs).

Important notice: the animation provided in this paper are mpeg files with the extension .mpeg, the size of the file being provided. You will therefore need a mpeg viewer like xanim or mpeg_play to enjoy the animation.

1. Introduction

Parallel robots have been extensively studied this recent years and are now starting to appear as commercial products for various applications, hence the interest for their optimal design. Among other criterion checking singularity is an important part of the design process. In this paper we consider a Gough-type 6 d.o.f. parallel manipulator (figure 1) constituted of a fixed base plate and a mobile plate connected by 6 articulated and extensible links.

**Figure 1:** Gough platform
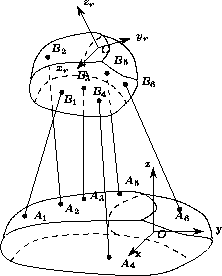
$\begin{figure} \begin{center} \unitlength 0.8cm \input{/u/caphorn/0/saga/merlet/Dessin/Robot/ssm_general.ltex} \end{center}\end{figure}$

The pose of the platform may be adjusted by changing the length of the six legs as shown in the following animation (mpeg file, 184 Kb).

A reference frame (O,x,y,z) is attached to the base and a mobile frame (C,x_r,y_r,z_r) is attached to the moving platform. The leg i is attached to the base with a ball-and-socket joint whose center is A_i, while it is attached to the moving platform with an universal joint whose center is B_i. The coordinates of A_i in the reference frame will be denoted by x_{A_i}, y_{A_i}, z_{A_i}, while the coordinates of B_i in the mobile frame are x_{B_i}, y_{B_i}, z_{B_i} (the index i may be omitted in the next sections). For a given robot these coordinates are assumed to be known. Let $\rho_i$ be the leg lengths (the distance between A_i and B_i), $\mbox{\boldmath$X$ }$ a 6-dimensional vector defining the pose of the end-effector: the three first components of $\mbox{\boldmath$X$ }$ are the coordinates of C in the reference frame, while the three last components are three parameters describing the orientation of the end-effector. In this paper we will use the Euler angles $\psi, \theta, \phi$ : the mobile frame is derived from the reference frame by first a rotation around the zaxis with an angle $\psi$ , then a rotation around the new x axis with an angle $\theta$ and finally a rotation around the new z axis with an angle $\phi$ (figure 2). Note that the use of Euler's angles is not compulsory for the algorithms described in this paper: any other orientation representation may be used.

**Figure 2:** Euler's angle for representing the orientation
$\begin{figure} \begin{center} \input{/u/caphorn/0/saga/merlet/Dessin/Mecanisme/euler.ltex} \end{center}\end{figure}$

2. Singular configurations

2.1 Inverse jacobian matrix

For a Gough platform it is easy to establish the inverse kinematics as:

$\begin{displaymath}\mbox{\boldmath$\rho$ }=\mbox{\boldmath$F(\mbox{\boldmath$X$ })$ } \end{displaymath}$

(1)

where $\mbox{\boldmath$\rho$ }$ is the vector of the leg lengths and $\mbox{\boldmath$X$ }$ the generalized coordinates of the platform. By an appropriate derivation we may obtain the relation between the articular velocities $\dot{\mbox{\boldmath$\rho$ }}$ and the platform velocities $\dot{\mbox{\boldmath$X$ }}$ as:

$\begin{displaymath}\dot{\mbox{\boldmath$\rho$ }}=J^{-1}\dot{\mbox{\boldmath$X$ }} \end{displaymath}$

(2)

where J^-1 is the inverse jacobian matrix of the robot. A row of this matrix may be written as:

$\begin{displaymath}J^{-1}_i = \frac{\mbox{\boldmath$A_iB_i$ }}{\rho_i}~~~~~\mbox{\boldmath$CB_i$ }\times \frac{\mbox{\boldmath$A_iB_i$ }}{\rho_i} \end{displaymath}$

(3)

A parallel singular configuration is defined as the configuration where the determinant of J^-1 vanishes. The importance of determining if there is any singular configuration in the workspace of the robot may be illustrated by considering the articular forces $\mbox{\boldmath$\tau$ }$ in the legs for a given load on the platform $\mbox{\boldmath${\cal F}$ }$ . The relation between these two quantities may be written as:

$\begin{displaymath}\mbox{\boldmath${\cal F}$ }=J^{-T} \mbox{\boldmath$\tau$ } \end{displaymath}$

(4)

To determine the components of $\mbox{\boldmath$\tau$ }$ it is necessary to solve the above linear system. Each of these components will be obtained as:

$\begin{displaymath}\tau_i = \frac{..}{\vert J^{-T}\vert} \end{displaymath}$

(5)

Hence at a singular configuration the articular forces may go to infinity, causing a breakdown of the robot.

Finding all the singular configurations of a given robot is a difficult task: indeed, although the inverse jacobian matrix is known, expansion of its determinant leads to an huge expression [2] which is difficult to use. Another approach is based on Grassmann line geometry and has been successful to determine all the possible relations on the posture parameters leading to a singularity [3]. Another area of work is the determination of the geometry such that the robot remains always in a singular configuration [7].

But from the design view point we are more interested in the following question: is there a singularity(s) in a given workspace of a given robot?. The designer may be interested either by a binary answer (yes or no) or by a more precise answer (the locations of the singularities) Our algorithms will be able to provide both types of answers, although only approximatively for the later case. To the best of our knowledge the former problem has not yet been addressed in the literature for 6 d.o.f. robot. Related works deal with conditioning index (like the condition number of the inverse jacobian matrix estimated over the whole workspace [1]). But this index is usually estimated by a discrete method over the whole workspace and henceforth may fail to locate singularities.

2.2 Semi inverse jacobian matrix

Let M be the 6 by 6 matrix, called the semi inverse jacobian matrix, whose rows are defined by:

$\begin{displaymath}M_i = \mbox{\boldmath$A_iB_i$ }~~~~~\mbox{\boldmath$CB_i$ }\times \mbox{\boldmath$A_iB_i$ } \end{displaymath}$

(6)

According to equations (3, 6) we may see that:

$\begin{displaymath}\vert J^{-1}\vert=\frac{\vert M\vert}{\prod_{i =1}^{i =6}\rho_i} \end{displaymath}$

(7)

Therefore the singular configuration may also be defined as the configuration for which |M|=0.

3. Existence of a singular configuration

We consider here a workspace W defined as a closed region in the 6-dimensional generalized coordinates space. We consider a point X₁ taken at random in W. We compute |M| at point X₁ and we will assume, without loss of generality that |M(X₁)| is greater than zero. Let us assume that we are able to find a point X₂ (or a set of points), in the same component of the workspace than X₁, such that |M(X₂)| < 0. As |M| is a real valued continuous and differentiable function, then any path from X₁ to X₂ will have a point X_s for which |M(X_s)|=0, which means that X_s is a singular configuration of the robot. As X₁, X₂ lie in the same component we may find a point X_s which lie in the workspace of the robot. Hence as soon as a point X₂ has been determined we know that there is a singular configuration in the workspace of the robot.

The purpose of the following sections is to present algorithms which are able to determine a pair of points X₁, X₂, if any exist. If such pair is found, then we have proven the existence of at least a singular configuration within the workspace and if no such pair has been found, then we will have proven that the workspace is singularity-free.

4. Workspace and extended box

4.1 Extended box

We define an extended box (or EB for short) as a pair of element: a cartesian box, which represent the possible locations of the end-effector, and a set of three ranges, one for each of the rotation angles. An EB is therefore composed of a location part (the box) and an orientation part and defines a 6D workspace for the robot.

4.2 Bisection of an extended box

In the sequel we will use an operator for an EB called bisection. This operator takes as input an EB and outputs 64 new EBs which are included in the initial EB. They are obtained by first splitting in half all the 6 ranges $I_1,\ldots,I_6$ which define the input EB. Thus if I_i =[a_i,b_i] we get two new ranges I_i1,I_i2 with

I_i1=[a_i,(a_i+b_i)/2] I_i2=[(a_i+b_i)/2,b_i]

The new EBs are then obtained by considering all the possible combinations of the new ranges of the type I_1j,I_2k,I_3l,I_4m,I_5n,I_6o where all the second index have a value 1 or 2. For example if the input EB is defined by the following ranges:

[-10,10], [-10,10], [40,50], [0,10], [0,0], [0,0]

then the output of the bisection will be the 16 EBs defined by:

$\begin{eqnarray*}&&[-10,0], [-10,0], [40,45], [0,5], [0,0], [0,0]\\ &&[-10,0], ... ... [0,0], [0,0]\\ &&[0,10], [0,10], [45,50], [5,10], [0,0], [0,0] \end{eqnarray*}$

Note that if the input EB has $n \le 6$ non constant ranges, then the bisection process will produce 2ⁿ new EB.

4.3 Singularity detection in a workspace

Consider an EB ${\cal B}$ and let assume that we have an algorithm A $({\cal B})$ which is able to determine first a lower and an upper bound of |M| for any pose within the EB ${\cal B}$ and will then return:

1, if the lower bound is positive
-1, if the upper bound is negative
0, if the lower bound is negative and the upper bound is positive

The bounds provided by the A algorithm may be overestimated but should be exact if the EB is reduced to one pose. The purpose of this section is to show that then we are able to determine if a singularity occurs within any type of workspace.

4.3.1 Singularity in a generalized coordinates workspace

Let assume that we want to check the presence of singularity in a workspace W defined by a 3D volume V describing the possible location of the center of the end-effector and three ranges $I_{\psi}, I_{\theta}, I_{\phi}$ which describe the possible values of the orientation angles. Clearly V may be approximated by a set of EB. For example the following animation (mpeg file, 233 Kb) shows how a sphere may be approximated using an increasing number of cartesian boxes.

Let us assume now that we are able to design a test algorithm T $({\cal B})$ which enable to determine if for the EB ${\cal B}$ :

1.: the location part of ${\cal B}$ is fully inside V
2.: the location part of ${\cal B}$ is fully outside V
3.: the location part of ${\cal B}$ is partially inside V

The algorithm T will return an integer which may 1, 2 or 3 according to the status of the location part with respect to V.

Using the algorithms A and T we are able to design an algorithm which enable to determine if a singularity occur within W. The algorithm start by computing a list S= $\{{\cal B}_0, {\cal B}_1, \ldots {\cal B}_{n-1}\}$ of n EBs such that the union of the location part of the EBs in the list is an approximation of the volume V, strictly including V, while the orientation part of each EB is simply defined as the range $I_{\psi}, I_{\theta}, I_{\phi}$ . We will then use two flags f_-, f₊ which will be initialized to 0 and will be set to 1 as soon as an EB for which the upper (lower) bound of |M| is negative (positive) is encountered during the algorithm. We may now describe the different steps followed by the algorithm at iteration k, the algorithm starting at iteration 0:

1.: if k>n-1 return NO SINGULARITY
2.: if T $({\cal B}_k)=2$ then k=k+1 and reiterate
3.: if A $({\cal B}_k)=1$ and T $({\cal B}_k)=1$ then set f₊ to 1

if f_-=1 then return SINGULARITY
otherwise k=k+1 and reiterate
4.: if A $({\cal B}_k)=-1$ and T $({\cal B}_k)=1$ then set f_- to 1

if f₊=1 then return SINGULARITY
otherwise k=k+1 and reiterate
5.: if T $({\cal B}_k)=3$ or A $({\cal B}_k)=0$ bisect ${\cal B}_k$ which create up to 64 new EBs. These new EBs are put at the end of the list S whose number of elements is updated (n=n+64), k=k+1 and reiterate

Basically this algorithm just consider each EB of the list sequentially. Flags are set as soon as an EB included in W is such that |M| has a constant sign. As soon we have encountered an EB with positive |M| and an EB with negative |M| we may state that a singularity occurs within W. During the iteration we will encounter EBs which are only partially inside W, or fully inside W but with bounds on |M| which have opposite sign. In that case we just bisect the EB and the resulting EBs are added to the list.

The algorithm stop either if a singularity has been detected or when all the elements of S have been considered, in which case there is no singularity in W.

4.3.2 Singularity in an articular workspace

Let us assume now that the workspace is not defined in term of generalized coordinates but in term of articular coordinates i.e. as all the poses X for which the leg lengths satisfy:

$\begin{displaymath}\rho_{min}^i \le \rho^i(X) \le \rho_{max}^i \end{displaymath}$

in which $\rho^i(X)$ denote the length of leg i at pose X and $\rho_{min}^i,\rho_{max}^i$ the minimal and maximal lengths of leg i. In other words we want to detect if a singularity occur within the reachable workspace of the robot.

Basically we will use exactly the same algorithm than in the previous section, with only a few modifications.

The first modification will be related to the algorithm T: we will need here an algorithm which enable to determine first what will be the extremal values of the leg lengths for any pose within an EB. This algorithm will be presented in section 5.2 but let us assume that such an algorithm is available. Then the design of T is quite straightforward. Indeed, let $\rho^i_m(B),\rho ^i_M(B)$ denote the minimal and maximal value of the length of leg i for the EB ${\cal B}$ , as computed by the algorithm. Then algorithm T will be

if for all legs $\rho_{min}^i \le \rho^i_m(B), \rho ^i_M(B) \le \rho_{max}^i$ then return 1

if for at least one leg we have $\rho^i_m(B) >\rho_{max}^i$ or $\rho ^i_M(B) < \rho_{min}^i$ then return 2

otherwise return 3

Note that it is not necessary to compute the exact values of $\rho^i_m(B), \rho ^i_M(B)$ , except in the case where ${\cal B}$ is reduced to a pose. Only lower and upper bounds on the minimal and maximal values are necessary. Indeed, the only consequence of an error on the estimation of these extremal values is that the algorithm T may return a status 3 for an EB which real status is 1. In the algorithm an EB with status 3 will be bisected until the status of the new EBs is either 1 or 2. If the real status of the EB is 1, then after a few bisection all the EBs will have status 1.

The second modification of the previous algorithm is to determine the initial value of the list S. This problem may be solved by finding an EB whose location part is a bounding box of the reachable workspace. Indeed for the orientation part as we deal with angle we have natural bounds on the range with the interval $[0, 2\pi$ ]. Various methods may be used for this purpose, but a very simple method enable to determine such a bounding box, although largely overestimated. To illustrate this method we will calculate a bound of the maximum value of the x coordinates of the point C of the moving platform or in other words the maximum value of the x component of the vector $\mbox{\boldmath$OC$ }$ . This vector may be written as:

$\begin{displaymath}\mbox{\boldmath$OC$ }=\mbox{\boldmath$OA$ }+\mbox{\boldmath$AB$ }+\mbox{\boldmath$BC$ } \end{displaymath}$

The norm $\vert\vert\mbox{\boldmath$AB$ }\vert\vert$ cannot be larger than $\rho_{max}$ while the norm $\vert\vert\mbox{\boldmath$BC$ }\vert\vert$ is the fixed distance d_CB between C and B. As a consequence, if x_A is the x component of $\mbox{\boldmath$OA$ }$ , then the x component of $\mbox{\boldmath$OC$ }$ cannot be larger than $x_A+\rho_{max}+d_{CB}$ . Let d_i be the value of $x_{A_i}+\rho_{max}^i+d_{CB_i}$ obtained for leg i . Then an upper bound of the maximal value of the x component of $\mbox{\boldmath$OC$ }$ is simply the minimum of the d_i. A similar procedure may be used to determine a lower bound of the minimal value of the x component of $\mbox{\boldmath$OC$ }$ and the process may be repeated for the y and z components. This will give clearly a largely over-estimated EB for the workspace but the calculation is quite simple.

With this initialization of S and by using the new T algorithm we may now use the previously described singularity detection algorithm to find if a singularity occur within an articular workspace.

More precisely if the previous algorithm does not detect a singularity then we may state that there is no singularity in the articular workspace. On the contrary let us assume that we have detected 2 EB in the articular workspace for which |M|>0 and |M|<0. A singularity will occur in the articular workspace only if these two regions belong to the same connected component of the articular workspace. Currently, to the best of my knowledge, there is no known method that may ensure that the 2 EBs belong to the same connected component. However a partial answer may be obtained by using two algorithms:

the first one enable to test if a singularity occur on a specific trajectory between two given poses [5]. The trajectory is defined as six successive elementary trajectories for which a linear interpolation between the first and second pose is performed on only one of the pose parameters
the second algorithm enable to verify if a trajectory lie inside the articular workspace [4]

We consider two poses, one belonging to the first EB, the second one to the second EB. Using the second algorithm we verify that the trajectory defined in the first algorithm lie in the articular workspace. If this is the case, then there is a singularity in the articular workspace, whose location is determined by the first algorithm. If the trajectory is not inside the articular workspace we cannot conclude.

4.3.3 Summary

Using the results of the previous two sections we are able to determine if a singularity occurs within any type of workspace either being defined in term of generalized coordinates or in term of articular coordinates, as soon as we have an algorithm which enable to determine if the lower and upper bound of |M| for any pose within an EB. The design of such an algorithm will be addressed in a later section, as soon as we have presented a mathematical tool which play a major role in our approach.

We must however mention a possible problem for these algorithms which occurs when a singularity is located exactly on the border of the workspace. Indeed in that case the number of EB of the list S will theoretically go to infinity as the algorithm will stop only when it will encounter the EB reduced to the singular pose.

5. Interval analysis

5.1 Principle

As we have seen in the previous section detecting singular configurations amounts to be able to find two EBs such that |M| for any pose in the EBs has a constant sign, this sign being opposite for the EBs. To ensure that |M| has a constant sign over an EB we may compute the minimal and maximal value of |M| for all the poses included in the EB. It must be noted that it is not necessary to compute exactly these extremal values: lower bound for the minimal value and upper bound for the maximal value will be sufficient.

Interval analysis [6] is a method that is able to deal with the problem of determining bounds on a function. Interval analysis is similar to real analysis except that real variables are replaced by intervals and that specific rules are used for each basic arithmetic operations.

More generally if $X_i=[\underline{x_i},\overline{x_i}]$ with $\underline{x_i} \le \overline{x_i}$ denotes an interval it is possible to define all the arithmetic operators (and more complex functions) for intervals. For example the "+" operator for intervals will be defined as:

$\begin{displaymath}X_1+X_2=[\underline{x_1}+\underline{x_2},\overline{x_1}+\overline{x_2}] \end{displaymath}$

while the multiplication operator is:

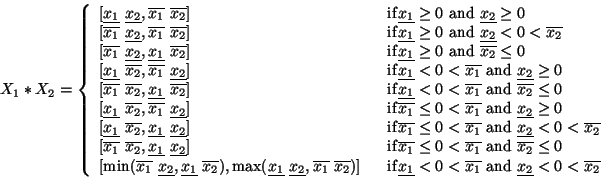
$\begin{displaymath}X_1 * X_2=\left\{ \begin{array}{ll} [\underline{x_1}~\underl... ...and}~\underline{x_2}< 0<\overline{x_2}\\ \end{array} \right. \end{displaymath}$

Consider now a very simple example of interval analysis: let the function x²+x for which we want to find the extremal values when x lie in the range [-1,0]. We consider each monomial of this function and compute its extremum, which lead to $x^2 \in [0,1]$ , $x \in [-1,0]$ . Then the upper bound of the sum is computed as the sum of the upper bound of each interval while the minimum is obtained as the sum of the lower bound.

x²+x=[0,1]+[-1,0]=[-1,1]

The way the monomials in an expression may be considered is not unique (in term of interval analysis we say that there are different evaluation functions). For example we may have used the Horner (or "nested") form of the previous function and get the following result:

$\begin{displaymath}x^2+x=x(x+1)=[-1,0]\times [0,1]=[-1,0] \end{displaymath}$

We notice here that the Horner form leads to a better estimation of the maximum (the real extremum being [-1/4,0]). This is true only if the range on the variable is not too large. For example if $x\in [-1,10]$ we get:

$\begin{eqnarray*}&&x^2+x=[0,100]+[-1,10]=[-1,110]\\ &&x(x+1)=[-1,10]\times[0,11]=[-11,110] \end{eqnarray*}$

A good point of interval analysis is that it can take into account round-off errors: result obtained through interval analysis may be guaranteed: the interval which is the result of operations on a set of interval is guaranteed to include the exact interval as computed using exact arithmetics. For example assume that during a computation we have to deal with the number f=1/3: there is clearly no exact floating point representation of this number. Using interval representation this number will be represented on a SUN workstation by the interval:

[0.333333333333333259318465,0.3333333333333333703407675]

as the first number is the largest machine floating point number lower than 1/3 and the second number if smallest machine floating point number greater than 1/3. Consequently any further operation with f will lead to an interval which is guaranteed to include the real result. For example multiplying f by 3 will lead to the interval:

[0.9999999999999997779553951,1.000000000000000222044605]

Numerous packages of interval analysis are available. In our implementation we are using the BIAS/PROFIL package.

5.2 Example of use of interval analysis

As we have seen in a previous section the detection of singularity in an articular workspace is possible as soon as we have an algorithm which is able to calculate a lower and an upper bound on the leg lengths for any pose in an EB. Interval analysis may be used for that purpose. Indeed the length of a leg is defined as the norm of the vector $\mbox{\boldmath$AB$ }$ . We may write this norm as:

$\begin{displaymath}\vert\vert\mbox{\boldmath$AB$ }\vert\vert=\vert\vert\mbox{\bo... ...th$AO$ }+\mbox{\boldmath$OC$ }+\mbox{\boldmath$CB$ }\vert\vert \end{displaymath}$

Using the rotation matrix R and the vector CB_r which define the coordinates of B in the mobile frame, this equation may be written as:

$\begin{displaymath}\vert\vert\mbox{\boldmath$AB$ }\vert\vert=\vert\vert\mbox{\bo... ...AO$ }+\mbox{\boldmath$OC$ }+R\mbox{\boldmath$CB_r$ }\vert\vert \end{displaymath}$

The three components of the vector $\mbox{\boldmath$AB$ }$ may be written as:

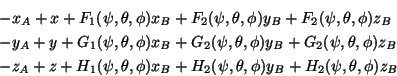
$\begin{eqnarray*}&&-x_A+x+F_1(\psi,\theta,\phi)x_B+F_2(\psi,\theta,\phi)y_B+ F_... ...ta,\phi)x_B+H_2(\psi,\theta,\phi)y_B+ H_2(\psi,\theta,\phi)z_B \end{eqnarray*}$

If the unknowns $x, y, z, \psi, \theta, \phi$ are defined in terms of intervals each of the component of the vector $\mbox{\boldmath$AB$ }$ may also be defined in terms of intervals as:

$\begin{eqnarray*}A_1&=&[-x_A,-x_A]+[\underline{x},\overline{x}]+ [\underline{F_1... ...ine{H_2},\overline{H_2}]y_B+ [\underline{H_3},\overline{H_3}]z_B \end{eqnarray*}$

In turn the norm of $\mbox{\boldmath$AB$ }$ may be calculated in interval terms as:

$\begin{displaymath}[\vert\vert\mbox{\boldmath$AB$ }\vert\vert]=\sqrt{A_1^2+A_2^2+A_3^2} \end{displaymath}$

and as a consequence we are able to compute a lower and an upper bound of the leg lengths for any pose in an EB.

6. Detecting singularity in an extended box

6.1 Finding bounds on the determinant for an extended box

Let us assume that we are dealing with an extended box defined by:

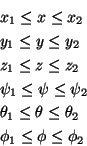
$\begin{eqnarray*}&&x_1 \le x \le x_2 \\ &&y_1 \le y \le y_2 \\ &&z_1 \le z \le... ...heta_1 \le \theta \le \theta_2 \\ &&\phi_1 \le \phi \le \phi_2 \end{eqnarray*}$

As all the unknowns in |M| are ranges we may apply interval analysis to obtain a lower bound of the minimal value of |M| and an upper bound on the maximal value of |M|, as soon as an analytical formulation of |M| is known. The problem is now to find this analytical formulation, under the constraint that we want to implement a general-purpose program that is able to deal with any robot geometry. For example the coordinates of the points A, B may be available in a file, called a robot file, that the program will read for updating the robot geometry.

A first approach to this problem may be to assume that these coordinates are only known symbolically as $x_{A_i}, y_{A_i},\ldots, z_{B_i}$ and to use a computer algebra program to compute a generic form of |M| as a function of the pose parameters and of $x_{A_i}, y_{A_i},\ldots, z_{B_i}$ . This determinant will be then decomposed as the sum of terms of the form:

$\begin{displaymath}\vert M\vert=\sum C_j(x_{A_i}, y_{A_i},\ldots, z_{B_i})F_j(x,y,z,\psi,\theta,\phi) \end{displaymath}$

Then as soon as the robot file has been read it will be possible to plug in the numerical values of the A_i, B_i coordinates in the C_j coefficients. Then we will use interval analysis to compute the bounds of each term C_j()F_j() for the ranges defining the EB and finally add the resulting intervals for obtaining the bounds on |M|. Unfortunately this approach is quite impossible to use for a Gough platform. Indeed computer algebra program like MAPLE have difficulties to compute a generic form of |M|. Furthermore when MAPLE succeed we will get a very large expression i.e. the evaluation of the terms C_j will suffer from numerical errors, thereby leading to errors in the evaluation of the bounds on |M|.

We have used a second approach which mix formal and numerical computation. When running our algorithm we will first read the robot file, then we will write the coordinates of the A_i, B_i points in a MAPLE file called the coordinates file. The program will then start in background a MAPLE session, in which MAPLE will first read the coordinates file and then compute the semi-inverse jacobian and its determinant (which is at this step only a function of $x, y, z, \psi , \theta , \phi$ ). An example of such program is presented in the appendix. The MAPLE program will then decompose this determinant as a sum of terms of the form

$\begin{displaymath}F_j(x, y, z, \psi , \theta , \phi)=C_j x^iy^{J}z^k\cos^l(\psi... ...n^m(\psi)\cos^n(\theta)\sin^o(\theta)\cos^p(\phi)\sin^q(\phi) \end{displaymath}$

where C_j is a numerical constant. The MAPLE program will then write in a result file the number of terms F_j and a description of each term. This file will start with the number n of F_j followed by n lines constituted of i,J,k,l,m,n,o,p,q, C_j. For example the file:

 
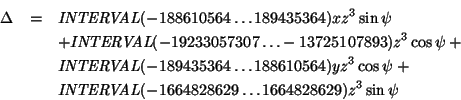
2 
0 0 1 0 0 2 0 0 2 1567854
0 0 2 0 0 2 1 0 0 -1279362

will indicate that the determinant |M| is:

$\begin{displaymath}1567854 z\cos^2(\theta)\cos^2(\phi)-1279362 z^2\cos^2(\theta)\sin(\theta) \end{displaymath}$

As soon as the result file is written the MAPLE session end. It must be noted that in some complex cases MAPLE may still have difficulties to calculate the analytical form of the determinant. It may be necessary to choose carefully the reference and mobile frame, so that the coordinates of the A, B points are as simple as possible (for example if some of these points are coplanar to choose the frames so that their z coordinates are 0). Note however that this MAPLE session has to be run only once for a given robot.

The main program will then read the result file and fill an appropriate data structure which enable to store each F_j. Each element of this structure represent an F_j and contain the value of the corresponding i,J,k,l,m,n,o,p,q, C_j. Consequently, by using the interval analysis package, we are able to evaluate the range of each F_j and consequently lower and upper bounds for |M|, this for the current EB.

We have still to deal with a numerical problem. The coordinates in the robot file are floating point numbers. If we use them directly in the MAPLE program numerical errors may occur in the calculation of the C_j. To solve this problem we will first use MAPLE to convert the floating point number representing a coordinate into an exact rational number. We will then compute the coefficients C_j of the F_j, which will be rational number. The advantage is that MAPLE computations with rational number are exact. As soon as all the C_jhave been computed we will calculate the least common multiple of all the denominators of the C_j and then multiply each C_j by this number. The resulting number is an integer which is stored as C_j in our data structure. This guarantee that the analytical formulation that is stored is an exact representation of |M|. As an example we present the coordinates file for a robot that will be used in the example:

 
xa1:=convert(-9,rational,exact):
ya1:=convert(9,rational,exact):
za1:=convert(0,rational,exact):
xb1:=convert(-3,rational,exact):
yb1:=convert(7,rational,exact):
zb1:=convert(0,rational,exact):
xa2:=convert(9,rational,exact):
ya2:=convert(9,rational,exact):
za2:=convert(0,rational,exact):
xb2:=convert(3,rational,exact):
yb2:=convert(7,rational,exact):
zb2:=convert(0,rational,exact):
xa3:=convert(12,rational,exact):
ya3:=convert(-3,rational,exact):
za3:=convert(0,rational,exact):
xb3:=convert(7,rational,exact):
yb3:=convert(-1,rational,exact):
zb3:=convert(0,rational,exact):
xa4:=convert(3,rational,exact):
ya4:=convert(-13,rational,exact):
za4:=convert(0,rational,exact):
xb4:=convert(4,rational,exact):
yb4:=convert(-6,rational,exact):
zb4:=convert(0,rational,exact):
xa5:=convert(-3,rational,exact):
ya5:=convert(-13,rational,exact):
za5:=convert(0,rational,exact):
xb5:=convert(-4,rational,exact):
yb5:=convert(-6,rational,exact):
zb5:=convert(0,rational,exact):
xa6:=convert(-12,rational,exact):
ya6:=convert(-3,rational,exact):
za6:=convert(0,rational,exact):
xb6:=convert(-7,rational,exact):
yb6:=convert(-1,rational,exact):
zb6:=convert(0,rational,exact):

But the use of integer numbers has a drawback: the calculation of |M| may lead to large integers for the coefficients C_j, which will exceed the largest integers available in a computer. Consider, for example, the robot whose coordinates are computed as rational number by MAPLE:

 
 xa1:=convert(-12.758,rational,exact);
                                        -6379
                                 xa1 := -----
                                         500

 ya1:=convert(3.902,rational,exact);
                                         1951
                                  ya1 := ----
                                         500

 za1:=convert(0,rational,exact);
                                   za1 := 0

 xb1:=convert(-7.8218,rational,exact);
                                        -39109
                                 xb1 := ------
                                         5000

 yb1:=convert(-1.052,rational,exact);
                                         -263
                                  yb1 := ----
                                         250

 zb1:=convert(0,rational,exact);
                                   zb1 := 0

 xa2:=convert(-9.758,rational,exact);
                                        -4879
                                 xa2 := -----
                                         500

 ya2:=convert(9.098,rational,exact);
                                         4549
                                  ya2 := ----
                                         500

 za2:=convert(0,rational,exact);
                                   za2 := 0

 xb2:=convert(-3,rational,exact);
                                   xb2 := -3

 yb2:=convert(7.3,rational,exact);
                                          73
                                   yb2 := --
                                          10

 zb2:=convert(0,rational,exact);
                                   zb2 := 0
 xa3:=convert(-3,rational,exact);
                                   xa3 := -3

 ya3:=convert(-13,rational,exact);
                                  ya3 := -13

 za3:=convert(0,rational,exact);
                                   za3 := 0

 xb3:=convert(-4.8218,rational,exact);
                                        -24109
                                 xb3 := ------
                                         5000

 yb3:=convert(-6.248,rational,exact);
                                         -781
                                  yb3 := ----
                                         125

 zb3:=convert(0,rational,exact);
                                   zb3 := 0

 xa4:=convert(3,rational,exact);
                                   xa4 := 3

 ya4:=convert(-13,rational,exact);
                                  ya4 := -13

 za4:=convert(0,rational,exact);
                                   za4 := 0

 xb4:=convert(4.8218,rational,exact);
                                        24109
                                 xb4 := -----
                                        5000

 yb4:=convert(-6.248,rational,exact);
                                         -781
                                  yb4 := ----
                                         125

 zb4:=convert(0,rational,exact);
                                   zb4 := 0

 xa5:=convert(9.758,rational,exact);
                                         4879
                                  xa5 := ----
                                         500

 ya5:=convert(9.098,rational,exact);
                                         4549
                                  ya5 := ----
                                         500

 za5:=convert(0,rational,exact);
                                   za5 := 0

 xb5:=convert(3,rational,exact);
                                   xb5 := 3

 yb5:=convert(7.3,rational,exact);
                                          73
                                   yb5 := --
                                          10

 zb5:=convert(0,rational,exact);
                                   zb5 := 0

 xa6:=convert(12.758,rational,exact);
                                         6379
                                  xa6 := ----
                                         500

 ya6:=convert(3.902,rational,exact);
                                         1951
                                  ya6 := ----
                                         500

 za6:=convert(0,rational,exact);
                                   za6 := 0

 xb6:=convert(7.8218,rational,exact);
                                        39109
                                 xb6 := -----
                                        5000

 yb6:=convert(-1.052,rational,exact);
                                         -263
                                  yb6 := ----
                                         250

 zb6:=convert(0,rational,exact);
                                   zb6 := 0

Using integer representation the determinant of M for $\psi = \phi =0$ will be

$\begin{eqnarray*}&&\vert M\vert= -19098060930659471193153794175\,y\sin(\theta) \... ...heta)-\\ &&431509284260148508225000000\,{y}^{2}z \sin^2(\theta) \end{eqnarray*}$

In that case it will be necessary to use floating point numbers, thereby introducing numerical errors in the calculation of |M|. To solve this problem we use in our implementation two possible representations for the coefficients C_j. If the computed coefficient is lower than the largest available integers then C_j is represented by this integer. Otherwise C_j is represented by an interval which is guaranteed to include the real value of the coefficient. This later representation has however some drawbacks:

it increases the computation time (the cost of multiplying two intervals is larger than multiplying an interval by an integer)
for very large coefficients C_j, the width of the interval used to represent a coefficient may be also large. As a consequence we may end up in a situation in which, even for a fixed pose, the evaluation interval of |M| may be a large interval which will include 0, in which case all of the algorithms presented in the following sections will fail.

6.2 Finding singularity in an extended box

As we are now able to determine bounds on |M| for any EB we may design an algorithm to detect if a singularity occurs within a given EB ${\cal B}$ . The algorithm will be basically similar to the one presented for the generalized coordinates workspace, the A algorithm being based on the procedure that compute bounds on |M|for the considered EB. The A algorithm will return:

0 if the upper bound of |M| is negative or the lower bound of |M| is positive
1 if the upper bound of |M| is positive and the lower bound of |M| is negative

We will then use two flags f_-, f₊ which will be initialized to 0. The flag f_- will be set to 1 if an EB with negative upper bound is encountered during the algorithm, while the flag f₊ will be set to 1 if an EB with positive lower bound is encountered (alternatively we may choose a specific pose in the initial EB, compute numerically the value of |M| for this pose and update the f_-, f₊ flags according to this value). The list S will be initialized with one EB ${\cal B}_0={\cal B}$ and n=1. At iteration k the algorithm proceed along the following steps:

1.

if k>n-1 return NO SINGULARITY

2.

if A $({\cal B}_k)=0$ then

update f_-,f₊ according to the bounds on |M|
if f_-=1 and f₊=1 return SINGULARITY
else k=k+1 and reiterate

3.

if A $({\cal B}_k)=1$ bisect ${\cal B}_k$ which create 64 new EBs. These new EBs are put at the end of the list S whose number of elements is updated (n=n+64), k=k+1 and reiterate

6.3 Improving the basic algorithm

Clearly the algorithm which determine the presence of singularity in an EB is a key point of all the algorithms which deal with the different types of workspace. A crucial point is the determination of the lower and upper bounds of |M|. Clearly the closer these bounds are to the real minimum and maximum values, the faster will be the algorithm. We have therefore to deal with a major problem of interval analysis which is that this method may lead to largely over-estimated bounds. We have noticed this phenomena for the function x²+x with $x \in [-1,0]$ : interval analysis leads to the lower bound -1 and upper bound 1, while the true result is -1/4, 0.

6.3.1 Improvement using the monotonicity

A possible way to improve the estimation of the lower and upper bounds of |M| is to use the monotonicity of this function. Indeed during the MAPLE session we have determined its analytical formulation and using the MAPLE function diff we are able to compute its derivatives with respect to the 6 pose parameters. As soon as these derivatives have been computed they are written in the result file in the same format than the one used for |M|. Using the corresponding data structure and interval analysis we are thus able to calculate bounds on the values of the 6 derivatives.

If all the 6 derivatives are such that their lower bound is negative and their upper bound is positive, then the extremal values of |M|are computed using interval analysis, the pose parameters being substituted by their ranges. Now assume that one derivative, for example the x derivative has a positive lower bound, while the other derivatives do not have a constant sign. This imply that |M| is a monotonous, increasing function of x. The minimum value for |M| will be obtained for $x= \underline{x}$ , while the maximum value will be obtained for $x=\overline{x}$ . Consequently to determine the bounds on |M| we will perform 2 interval analysis evaluations of |M|, the pose parameters ranges being successively:

$\begin{eqnarray*}&& [\underline{x},\underline{x}],[\underline{y},\overline{y}], ... ...ne{\theta},\overline{\theta}],[\underline{\phi},\overline{\phi}] \end{eqnarray*}$

in which the x parameter of the pose has now a constant value. But we still can improve these evaluations. Indeed we have estimated the range of the derivatives using the full ranges for the pose parameters. As the x parameter is now a constant the evaluation of one (or more) of the derivative, different from the xderivative, may have a constant sign. For example when performing the evaluation of the lower bound of |M| (which is obtained for $x=\underline{x}$ ) the derivative with respect to y may have a negative upper bound. This means that the lower bound is monotonously decreasing with respect to y. Consequently the lowest lower bound will be obtained for $x=\underline{x}$ and $y=\overline{y}$ and we may proceed similarly for the other variables.

For an algorithmic view point it may be seen that, as soon as one of the derivative of |M| has a constant sign when evaluated with the full ranges of the pose parameters, we have to perform a recursive evaluation of the lower and upper bound of |M|. This recursion will however be stopped in different cases:

as soon as all the 6 derivatives have a constant sign: in that case we are able to compute exactly the bounds on |M|. If these bounds have opposite sign then we may ensure that there is a singularity in the EB (see the example in section 11.4)
when the number of derivative with constant sign at some recursion level is the same than this number at the previous level
if the flag f_- has been set to 1 at some iteration of the algorithm and at the current recursion level the minimal value of |M| is positive (in which case a singularity occurs) or the maximal value of |M| is negative (in which case the current EB is discarded)
if the flag f₊ has been set to 1 at some iteration of the algorithm and at the current recursion level the maximal value of |M| is negative (in which case a singularity occurs) or the minimal value of |M| is positive (in which case the current EB is discarded)

Note also that it is interesting to store the range of the derivatives for each EB. Indeed if some of these derivatives have a constant sign and if the EB is bisected during the algorithm it will not be necessary to recompute the derivatives with constant sign for the new EB as they will also have a constant sign.

6.4 Improvement in the bisection process

A drawback of the proposed algorithms is that the number of EB generated during a run of the algorithm may increase exponentially (at each stage 64 new EBs are created, which in turn each lead to the creation of 64 new EBs). Consequently we may rapidly exceed the available memory of our computer.

But there are ways to manage more carefully the computer memory. The first possible way is an appropriate management of the list S. When an EB ${\cal B}$ is bisected instead of putting the 64 new EBs ${\cal B}_1,{\cal B}_2,\ldots,{\cal B}_{64}$ at the end of the list S, we may just substitute ${\cal B}$ by ${\cal B}_1$ and put the remaining EBs at the end of S, while keeping the current value of the pointer index of S. A further improvement is possible as follows: assume that the flags f_- has been set at a previous iteration of the algorithm; when bisecting we will substitute the current EB by the EB that has the highest probability of leading to an EB having a constant positive sign. This EB can be selected, for example, as the one having the largest positive upper bound or the lowest absolute value of the lower bound. This heuristic may enable to detect more rapidly a singularity

A second way to improve the memory management is to free the EBs in S which have been processed. Assume that we have defined a maximum number N of EB for S. As the algorithm proceeds we may end up at a stage where we are current processing the EB ${\cal B}_k$ of S while the total number N_s of EB in S is greater than N-64. If a bisection process has to be performed on ${\cal B}_k$ the total number of EB may exceed N. But the EB ${\cal B}_0,\ldots,{\cal B}_{k-1}$ in S have been processed so we may free k EB in the list in order to have a total number of EB in S, which is now N_s-k.

Another possible improvement is, when having to bisect an EB, to proceed only to a partial bisection i.e. to bisect not all the pose parameters. In our current implementation we bisect first only the pose parameters leading to a derivative of |M| which has a non constant sign. The idea is that bisecting only on these parameters may lead to a larger number of derivatives with constant sign and consequently to a better evaluation of |M|.

7. Approximation of the singular surfaces

Even for a well designed parallel manipulator it may occur that singularities exist within the reachable workspace, but outside the usually used workspace. It may still be interesting to determine approximatively the regions of the workspace where singularities occur, for example to design a path planning method which will be able to manage trajectories in the dangerous region.

We have designed an algorithm which enable to determine an approximation of the singularity loci over a workspace defined in term of either generalized coordinates or articular coordinates. This approximation is in fact a list L of EB in which there may be singularities and the accuracy of the approximation is directly related to the volume of the location part of the EB, a parameter that we define at the beginning of the algorithm.

Basically the algorithm is similar to the algorithms presented in the previous sections. The only difference is that we check during the bisection process the volume of the EB resulting from the bisection. If this volume is lower than the fixed threshold and if the lower bound of |M| is negative while the upper bound is positive instead of storing the EB in S, we write a description of the EB in a file which will contain the list L.

To decrease the computation time of this algorithm we have implemented an incremental version. A first run enable to provide a very rough approximation of the singularity surfaces. In the later run the accuracy threshold will be decreased but the algorithm will consider only the EB of the list L which has been obtained at the previous run, thereby avoiding unnecessary computation.

The following animation (mpeg file, 166 Kb) shows an example of singularity surfaces with decreasing volume of the EB for the robot 1 and the reachable workspace when the angle $\phi$ is equal to zero.

Note that two different types of EB are present in the list L:

1.: EB for which all the derivatives have constant sign and for which the lower bound of |M| is negative while the upper bound is positive: a singularity is present in the EB
2.: EB for which not all the derivatives have constant sign and for which the lower bound of |M| is negative while the upper bound is positive: we are not sure if a singularity occurs in this EB

8. Parallel implementation

Clearly the above algorithms have an inherent parallel structure that may be used in order to reduce the computation time. Let us assume that an array of n computers connected via a network is available. One of the computer will run a main program that will dispatch to the other computers the treatment of the extended boxes as a child process. For example, if the initial list S has more than one EB the first n-1 EBs will be dispatched to the n-1 available computers, while the main program will deal with the n-th EB. A communication stream will be open between the main program and the n-1 computers so that as soon as one of the child process has been completed, its result is transmitted to the main program. According to this result a singularity may have been detected, otherwise the main program will start new child process for each free computer, with as input, an unprocessed EB in the list S of the main program. Note that there are available softwares (e.g. like PVM) to manage this parallel implementation.

9. Dealing with uncertainties in the location of the joints

Up to now we have assumed that the geometry of the robot was perfectly known. In practice however manufacturing tolerances lead to uncertainties in the locations of the joints. We may assume that the coordinates of the joints may be represented by ranges instead of floating point numbers, the purpose being to determine if there is a singularity in the workspace for any real robot whose joint coordinates belong to the ranges. We may still theoretically proceed with the calculation of the determinant of the semi inverse jacobian matrix, the coefficients C_j being now ranges. But there are drawbacks in this approach:

each element of the semi inverse jacobian is a function of the pose parameters with coefficients which are ranges. Hence, when computing the determinant we will no more get automatic simplifications in the coefficients. The determinant may become a so large expression that MAPLE cannot handle it
when expanding the determinant and computing the coefficients C_j each joint coordinate will be considered as independent, which may lead to large over estimation of the C_j. For example assume that a coefficient C_j has the analytical expression which is obtained by summing up x_A₁x_A₂ and -x_A₁x_A₂. Although the real value of C_j is zero, the interval evaluation of this sum will not be zero

To illustrate these two points we have considered the example of robot 1 and have assumed that each of its joint coordinate may have an error of $\pm$ 0.01. MAPLE was unable to calculate the determinant when at least one of the pose parameters in the workspace description was not zero. Assume now that we have $\theta = \phi =0$ . For fixed values of the joint coordinates the determinant $\Delta$ is

$\begin{displaymath}\Delta = -z^3\cos\psi \end{displaymath}$

while if we assume that the joint coordinates are ranges, $\Delta$ is

$\begin{eqnarray*}\Delta &=&{\it INTERVAL}({-188610564\ldots 189435364})xz^{3}\si... ... && {\it INTERVAL}({-1664828629\ldots 1664828629})z^{3}\sin\psi \end{eqnarray*}$

But for this simplified workspace we are still able to show that there is no singularity in the workspace defined by the range x, y in [-15,15], z in [45,50] and $\psi$ in [-15,15] degree.

10. Dealing with other mechanical architectures

All the previous algorithms have been explained and implemented to deal with a Gough platform but clearly will remain similar for any type of parallel robots for which the inverse kinematics has only one solution. There are only two changes that have to be made to accommodate a different architecture:

1.: provide a MAPLE program that enable to compute the determinant of the inverse jacobian of the robot. Note that in this MAPLE file you may use another representation of the orientation as soon as three angles are used (for compatibility reasons with the current implementation of the algorithms). This is the only change if you are dealing with a workspace expressed in term of generalized coordinates
2.: if you are dealing with articular workspace, provide a software module that enable to check if an EB is either fully inside, fully outside or partially inside the articular workspace

On the opposite the algorithm may be more difficult to use for parallel robot with multiple solutions to the inverse kinematics. Indeed in that case the inverse jacobian matrix is a function not only of the pose parameters, but also of the articular coordinates. Consider for example the case of a robot with PRRS chains (figure 3), where the prismatic joint is actuated, leading to a motion of the A point (here along a vertical direction) while the length of link AB is fixed, B being connected to the mobile platform by a ball-and-socket joint. Example of motion for this type of mechanism is illustrated in the following animation (mpeg file, 241 Kb).

**Figure 3:** A robot with PRSS chains, the prismatic joint being actuated
$\begin{figure} \begin{center} \input{/u/caphorn/0/saga/merlet/Dessin/Robot/proto_robot.ltex} \end{center}\end{figure}$

If u is the unit vector which indicate the direction of motion of the prismatic joint (in our example u is (0,0,1)), then a row of the inverse jacobian matrix is:

$\begin{displaymath}\frac{\mbox{\boldmath$A_iB_i$ }}{{\bf u}.\mbox{\boldmath$A_iB... ... \mbox{\boldmath$A_iB_i$ }}{{\bf u}.\mbox{\boldmath$A_iB_i$ }} \end{displaymath}$

The inverse kinematics has up to 64 solutions. Indeed let consider only one chain for a given pose of the end-effector, and therefore a fixed location of B, and let l denote the length of link AB. The corresponding locations of A is obtained as the intersection of the sphere centered at B with radius l, with the line going through M and having u as unit vector. There are therefore two possible locations for A, A_m, A_n, which are characterized by the fact that A_m has a z coordinate larger than the one of B, while A_nhas a lower z coordinate, or equivalently that ${\bf u}.\mbox{\boldmath$A_mB$ }<0$ and ${\bf u}.\mbox{\boldmath$A_nB$ }>0$ . Being given limits on the motion of the prismatic joints we may retain only the inverse kinematics solution A_s for A such that ${\bf u}.\mbox{\boldmath$A_sB$ }>0$ . In that case the denominator of the inverse jacobian matrix is the product of the ${\bf u}.\mbox{\boldmath$A_sB$ }$ , and therefore has a strictly positive value. We may therefore consider as semi-inverse jacobian matrix the matrix which is obtained by taking only the numerator of each component of the inverse jacobian. Still the components of this matrix will contain articular coordinate terms. Indeed if $\lambda$ denote the articular coordinate of the chain the vector $\mbox{\boldmath$AB$ }$ may be written as:

$\begin{displaymath}\mbox{\boldmath$AB$ }=\mbox{\boldmath$AM$ }+\mbox{\boldmath$MB$ }= \lambda {\bf u}+\mbox{\boldmath$MB$ } \end{displaymath}$

M being a fixed point, $\mbox{\boldmath$MB$ }$ is therefore a function of only the pose parameters. Consequently vector $\mbox{\boldmath$AB$ }$ is a function of both the articular coordinates and the pose parameters and the determinant of the semi-inverse jacobian will be also a function of both sets of parameters. However this does not imply that the above algorithms cannot be used. Indeed being given an EB we can still use interval analysis to compute ranges for the articular coordinates, these ranges being used together with the ranges on the pose parameters to evaluate the bounds on the determinant. This has however a negative influence on the accuracy on the bounds, which is also worsened as the computation of the derivatives of the determinant with respect to the pose parameters will also be dependent on the articular coordinates. Consequently we may expect a much more larger computation time in that case.

11. Examples and computation time

The above algorithms have been implemented in C++ on a SUN Ultra 10 workstation under Unix-Solaris and on a PC laptop Dell Latitude CP 300 (300 Mhz) under linux. The computation time provided for the example have been obtained on these computers. They do not include the computation time of the MAPLE session. All the angle values are given in degree.

11.1 The considered robots

The coordinates of A and B of robot 1 are presented in the table 1.

Table 1: Coordinates of the A, B points for robot 1

	x_A	y_A	z_A	x_B	y_B	z_B
1	-9	9	0	-3	7	0
2	9	9	0	3	7	0
3	12	-3	0	7	-1	0
4	3	-13	0	4	-6	0
5	-3	-13	0	-4	-6	0
6	-12	-3	0	-7	-1	0

The minimal and maximal lengths of the legs are 55 and 60. This robot is presented in figure 4.

**Figure 4:** Robot 1
$\begin{figure} \begin{center} \input{/u/caphorn/0/saga/merlet/Dessin/Robot/debug_robot.ltex} \end{center}\end{figure}$

The coordinates of A and B of robot 2 are presented in the table 2.

Table 2: Coordinates of the A, B points for robot 2

	x_A	y_A	z_A	x_B	y_B	z_B
1	-9	9	0	-12	-3	0
2	9	9	0	12	-3	0
3	12	-3	0	9	9	0
4	3	-13	0	-3	-13	0
5	-3	-13	0	3	-13	0
6	-12	-3	0	-9	9	0

The minimal and maximal lengths of the legs are 55 and 60. This robot is presented in figure 5.

**Figure 5:** Robot 2
$\begin{figure} \begin{center} \input{/u/caphorn/0/saga/merlet/Dessin/Robot/gidding_robot.ltex} \end{center}\end{figure}$

We may also consider robot whose attachment point are not coplanar. The coordinates of A and B of robot 3 are presented in the table 3.

Table 3: Coordinates of the A, B points for robot 3

	x_A	y_A	z_A	x_B	y_B	z_B
1	-2539	1778	0	-657	-239	-100
2	2539	1778	500	657	-239	100
3	2809	1310	0	121	689	-100
4	270	-3088	500	-536	-449	100
5	-270	-3088	0	536	-449	-100
6	-2809	1310	500	-121	689	100

The minimal and maximal length for legs 1, 3, 5 are 3760, 4390, while for legs 2, 4, 6 they are 3545,4175. This robot is presented in figure 6.

**Figure 6:** Robot 3
$\begin{figure} \begin{center} \input{/u/caphorn/0/saga/merlet/Dessin/Robot/6x1_robot.ltex} \end{center}\end{figure}$

11.2 Singularity in an extended box

The following animation (mpeg file, 381 Kb) shows a typical run of the algorithm for robot 1 which determine if a singularity occurs within an EB: each image shows at each iteration the EB ${\cal B}_k,\ldots,{\cal B}_{n-1}$ which have not yet been considered in S. The initial EB ${\cal B}_0$ is progressively bisected, some of the resulting EB being eliminated as there is no singularity in them, until all the EB in the list have been considered, which means that there is no singularity in ${\cal B}_0$ . The considered EB is defined by the following range:

x	y	z	$\psi$	$\theta$	$\phi$
[-15,15]	[-15,15],	[45,50]	[-15,15]	[-15,15]	[-15,15]

For this extended box the absence of singularity is verified in the following computation time (in seconds):

Robot 1 (SUN)	Robot 1 (PC)	Robot 2 (SUN)	Robot 2 (PC)
51.41	24.61	2.35	0.87

We consider now the EB defined by the following range:

x	y	z	$\psi$	$\theta$	$\phi$
[-15,15]	[-15,15],	[45,50]	[-40,40]	[-40,40]	[-40,40]

For this extended box a singularity is detected for robot 1 and 2. A singularity is detected for robot 1 after examining 3 EB for a total of 296 EB while for robot 2 singularity detection occurs after having examined 1668 EB on a total of 3754. This verification is done in the following computation time (in seconds):

Robot 1 (SUN)	Robot 1 (PC)	Robot 2 (SUN)	Robot 2 (PC)
9.22	8.99	364.91	305.75

Singularity in an extended box have been also studied for robot 3. In the EB defined by [-200,200], [-200,200], [2800,3200], [-20,20], [-20,20], [-20,20] no singularity are detected in 19m5s on the SUN and 29mn11s on the PC. If we extend the orientation part of the EB to [-30,30] the computation time become 5h23mn on the SUN and 8h15mn on the PC.

11.3 Singularity in a sphere

We have also implemented the special case where the location part of the workspace is a sphere (basically the algorithm is similar to the articular workspace algorithm, the only change being the T algorithm which enable to test if an EB is fully inside, fully outside or partially outside the sphere).

For robot 1 and 2 and a sphere centered at (0,0,45) with radius 5, the orientation ranges being [-20,20], no singularity is detected. The computation time for robot 1 is 1mn31 on the SUN and 1mn34s on the PC. For robot 2 the computation time is 0.02s on the SUN and 0.05s on the PC. The following animation (mpeg file, 592Kb) shows as boxes the orientation part of the EB which remain to be processed during the run of the algorithm on robot 1 (the first box is therefore defined by [-20,20], [-20,20], [-20,20] and at the end of the algorithm no boxes are left as there is no singularity).

For robot 3 we have tested the presence of singularity in the sphere centered at (0,0,0,3000), the orientation ranges being [-20,20]. No singularity are detected in this workspace in a computation time of 6mn23s on the SUN and 10mn10s on the PC.

11.4 Singularity in an articular workspace

The following animation (mpeg file, 625 Kb) shows a typical run of the algorithm on the robot 1 which determine if a singularity occurs within the articular workspace where the angles $\psi$ and $\phi$ are equal to 0 while the range for the angle $\theta$ is [-40,40]: each image shows at each iteration the EBs ${\cal B}_k,\ldots,{\cal B}_{n-1}$ which have not yet been considered in S. The initial EB ${\cal B}_0$ is progressively bisected, some of the resulting EB being eliminated as there is no singularity in them, until all the EB in the list have been considered, which means that there is no singularity in ${\cal B}_0$ . For this extended box the absence of singularity is verified in the following computation time (in seconds):

Robot 1 (SUN)	Robot 1 (PC)	Robot 2 (SUN)	Robot 2 (PC)
6.54	3.71	0.36	0.11

A similar animation (mpeg file, 388 Kb) is shown for robot 3. Here we determine if a singularity occurs in the articular workspace constrained by $\phi =0$ , while the range for the angles $\psi$ , $\theta$ is [-20,20]: each image shows at each iteration the EB ${\cal B}_k,\ldots,{\cal B}_{n-1}$ which have not yet been considered in S. The initial EB ${\cal B}_0$ is progressively bisected, some of the resulting EB being eliminated as there is no singularity in them, until all the EB in the list have been considered, which means that there is no singularity in this articular workspace. The computation time is 46.54s on a SUN and 41.9s on a PC.

We may also consider a more general example where we consider the articular workspace as the set of poses for which $z\ge 40$ and the ranges on the orientation angles are [-40,40],[-40,40],[-40,40]. For this articular workspace the presence of a singularity is detected for robot 1 after examining 551 EBs for a total of 14696 EBs. Indeed for the EB numbered 551 the 6 derivatives have a constant sign which enable to compute exactly the bounds on |M|. These bounds have opposite sign, which imply that there is a singularity in the EB. These bounds are obtained for the following poses:

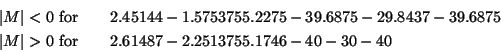
$\begin{eqnarray*}\vert M\vert<0~{\rm for} &&2.45144 -1.57537 55.2275 -39.6875 -2... ... \vert M\vert>0~{\rm for} &&2.61487 -2.25137 55.1746 -40 -30 -40 \end{eqnarray*}$

For robot 2, after examining 5752 EBs, there is no singularity in the articular workspace. This verification is done in the following computation time (in seconds):

Robot 1 (SUN)	Robot 1 (PC)	Robot 2 (SUN)	Robot 2 (PC)
351s	285s	14mn31s	11mn22s

For robot 3 we have investigated the presence of singularity in the articular workspace for which we have restricted the zcoordinates of the end-effector to be greater than 2000, and the Euler's angles to be in the range [-20,20]. The initial EB in S has the following ranges for the x, y, zcoordinates:

$\begin{displaymath}x \in [-1878.85,1644.15]~~~ y \in [-2674.69,1364.79]~~~z \in [2000,5096.24] \end{displaymath}$

After examining 9147 EBs no singularity is detected in this articular workspace: the computation time on the SUN workstation is 1h43mn and 2h19mn on a PC (this difference may be explained by the fact that for robot 3 the coefficients of the determinant are large, which lead to an extensive use of floating point arithmetics).

12. Conclusion

The algorithms proposed in this paper enable to solve a very important problem in the design process of a parallel robot. As may be seen in the benches the computation time is in general quite acceptable. However these algorithms can be clearly improved with respect to the computation time. Three main points should be addressed to reduce this time:

the representation of the constant coefficients appearing in the determinant: interval representation should be used only at the last resort as it increase substantially the computation time of the estimation of the bounds of the determinant
the evaluation of the bounds of the determinant: in our implementation the determinant is evaluated as:

$\begin{displaymath}\vert M\vert=\sum C_j(x_{A_i}, y_{A_i},\ldots, z_{B_i})F_j(x,y,z,\psi,\theta,\phi) \end{displaymath}$

Each of the F_j terms is evaluated independently, which leads to a large over estimation of the bounds. We should take into account the dependency between the terms in order to improve the evaluation
the bisection process should be more carefully managed in order to decrease the total number of EB for which the evaluation of the bounds of the determinant is performed

Another type of problem should be addressed: assuming that our algorithms has enable to establish that there is no singularity within a given workspace it may still happen that some poses in the workspace are "close" from a singularity. Establishing the minimal "distance" between the poses in the workspace and a singularity is a difficult problem as there is no distance, in the strict mathematical sense, that can be used to define how close a pose is from a singularity. However we may get an idea by using as index the absolute value of the determinant. It may be interesting when checking a workspace to determine the EB with the lowest value of this index. This will require a modification of our implementation as the estimation of the bounds of the determinant is stopped as soon as it has been checked that the extremal values have same sign. But these extremal values may be largely over estimated for one EB, while being almost exact for another one. Thus we cannot rely on these values to express a "distance" between the EB and a singularity. A possibility to deal with this problem will be to stop the evaluation of the minimal and maximal values of |M| for an EB only when the difference between these values is lower than a fixed threshold. But this will have a large impact on the computation time. Further work should therefore address the problem of determining the lowest value of the conditioning index as soon as there is no singularity in the workspace.

13. Appendix: MAPLE program

We present here an example of MAPLE program which may be used to compute the semi-jacobian matrix, its determinant and the derivative of this determinant.

 
with(linalg):

read(`/tmp/data`): #read the coordinates of the A, B points

#rotation matrix
rot:=array([[cos(p)*cos(h)-sin(p)*cos(t)*sin(h)
,-cos(p)*sin(h)-sin(p)*cos(t)*cos(h),
sin(p)*sin(t)],[sin(p)*cos(h)+cos(p)*cos(t)*sin(h),
-sin(p)*sin(h)+cos(p)*cos(t)*cos(h),-cos(p)*sin(t)],
[sin(t)*sin(h),sin(t)*cos(h),cos(t)]]):


OC:=array([x,y,z]):

#compute the vector AB, CB which appear in the jacobian
for i from 1 to 6 do
	OA.i:=array([xa.i,ya.i,za.i]):
	CBr.i:=array([xb.i,yb.i,zb.i]):
	CB.i:=multiply(rot,CBr.i):
	AB.i:=evalm(OC+CB.i-OA.i):
	ab.i:=array([AB.i[1],AB.i[2],AB.i[3]]):
od:

#semi-jacobian matrix

invjac:=array([
[ab1[1],ab1[2],ab1[3],(CB1[2]*ab1[3]-CB1[3]*ab1[2]),
(CB1[3]*ab1[1]-CB1[1]*ab1[3]),(CB1[1]*ab1[2]-CB1[2]*ab1[1])],
[ab2[1],ab2[2],ab2[3],(CB2[2]*ab2[3]-CB2[3]*ab2[2]),
(CB2[3]*ab2[1]-CB2[1]*ab2[3]),(CB2[1]*ab2[2]-CB2[2]*ab2[1])],
[ab3[1],ab3[2],ab3[3],(CB3[2]*ab3[3]-CB3[3]*ab3[2]),
(CB3[3]*ab3[1]-CB3[1]*ab3[3]),(CB3[1]*ab3[2]-CB3[2]*ab3[1])],
[ab4[1],ab4[2],ab4[3],(CB4[2]*ab4[3]-CB4[3]*ab4[2]),
(CB4[3]*ab4[1]-CB4[1]*ab4[3]),(CB4[1]*ab4[2]-CB4[2]*ab4[1])],
[ab5[1],ab5[2],ab5[3],(CB5[2]*ab5[3]-CB5[3]*ab5[2]),
(CB5[3]*ab5[1]-CB5[1]*ab5[3]),(CB5[1]*ab5[2]-CB5[2]*ab5[1])],
[ab6[1],ab6[2],ab6[3],(CB6[2]*ab6[3]-CB6[3]*ab6[2]),
(CB6[3]*ab6[1]-CB6[1]*ab6[3]),(CB6[1]*ab6[2]-CB6[2]*ab6[1])]]):

#we compute the determinant by expansion with respect
#to the first column

ew:=0:
for i from 1 to 6 do
	yy:=minor(invjac,i,1):
	rr.i:=det(yy):
	ew:=ew+(-1)^(i+1)*invjac[i,1]*rr.i:
od:

#if x,y,z,p,t,h have been assigned we need to unassign them to collect
x:='x':
y:='y':
z:='z':
p:='p':
t:='t':
h:='h':

fd:=open("/tmp/Coeff",WRITE):
ew1:=collect(ew,[x,y,z,sin(p),cos(p),sin(t),cos(t),sin(h),cos(h)],distributed):

#trigonometric simplification
print(`Simplifying determinant`);
ew1:=simplify(ew1,trig):
ew1:=numer(ew1):

#print in the result file the number of terms of the determinant
n:=nops(ew1):
if whattype(ew1)<>`+` then n:=1: fi:
fprintf(fd,`%d\n`,n):


#the determinant is ready and we write its expression in the result file
for i from 1 to n do
	u:=ew1:
	if n>1 then u:=op(i,ew1): fi:
	u1:=u:
	if u=0 then u:=1: fi:
	nx:=degree(u,x):
	ny:=degree(u,y):
	nz:=degree(u,z):
	nsp:=degree(u,sin(p)):
	ncp:=degree(u,cos(p)):
	nst:=degree(u,sin(t)):
	nct:=degree(u,cos(t)):
	nsh:=degree(u,sin(h)):
	nch:=degree(u,cos(h)):
	u:=u1:
	m:=nops(u);
	for j from 1 to m do
		uu:=op(j,u): 
		if type(uu,integer)=true then fac:=uu: break: fi:
	od:
	fprintf(fd,`%d %d %d %d %d %d %d %d %d %d\n`,nx,ny,nz,nsp,ncp,nst,nct,
		nsh,nch,fac):
od:

#in the sequel of this program we compute the derivative, here only
#the derivative with respect to x

ewn:=expand(diff(ew1,x)):
n:=nops(ewn):
if whattype(ewn)<>`+` then n:=1: fi:
if n>1 then
	ewn1:=simplify(ewn,trig):
	nn:=nops(ewn1):
	if whattype(ewn1)<>`+` then nn:=1: fi:
	if nn < n then
		ewn:=ewn1:
		n:=nn:
	fi:
fi:
fprintf(fd,`%d\n`,n):

for i from 1 to n do
	u:=ewn:
	if n>1 then u:=op(i,ewn): fi:
	u1:=u:
	if u=0 then u:=1: fi:
	nx:=degree(u,x):
	ny:=degree(u,y):
	nz:=degree(u,z):
	nsp:=degree(u,sin(p)):
	ncp:=degree(u,cos(p)):
	nst:=degree(u,sin(t)):
	nct:=degree(u,cos(t)):
	nsh:=degree(u,sin(h)):
	nch:=degree(u,cos(h)):
	u:=u1:
	m:=nops(u);
	for j from 1 to m do
		uu:=op(j,u): 
		if type(uu,integer)=true then fac:=uu: break: fi:
	od:
	fprintf(fd,`%d %d %d %d %d %d %d %d %d %d\n`,nx,ny,nz,nsp,ncp,nst,nct,
		nsh,nch,fac):
od:

#here you have to do the same job with respect to the variable
#y,z,p,t,h

fclose(fd):

Bibliography

1: Gosselin C. and Angeles J.
The optimum kinematic design of a spherical three-degree-of-freedom parallel manipulator.
J. of Mechanisms, Transmissions and Automation in Design, 111(2):202-207, 1989.
2: Mayer St-Onge B. and Gosselin C.
Singularity analysis and representation of spatial six-dof parallel manipulators.
In J. Lenarcic V. Parenti-Castelli, editor, Recent Advances in Robot Kinematics, pages 389-398. Kluwer, 1996.
3: Merlet J-P.
Singular configurations of parallel manipulators and Grassmann geometry.
Int. J. of Robotics Research, 8(5):45-56, Octobre 1989
4: Merlet J-P.
Trajectory verification in the workspace for parallel manipulators.
Int. J. of Robotics Research, 13(4):326-333, Août 1994
5: Merlet J-P.
Estimation efficace des caractéristiques de robots paralèlles: Extremums des raideurs et des coordonnées, vitesses, forces articulaires et singularités dans un espace de travail en translation.
Research Report 3243, INRIA, Septembre 1997
6: Moore R.E.
Methods and Applications of Interval Analysis.
SIAM Studies in Applied Mathematics, 1979.
7: Zsombor-Murray P., Husty M., and Hartmann D.
Singular Stewart-Gough platforms with spherocylindrical and spheroconical hip joint trajectories.
In 9th World Congress on the Theory of Machines and Mechanisms, pages 1886-1890, Milan, 30 Août-2 Septembre, 1995

J-P. Merlet