Combinatoire et prédicats
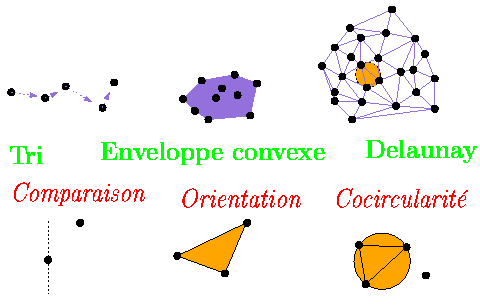
La plupart des algorithmes peuvent être vu sous un angle combinatoire. L'information calculée est de nature discrète, par exemple, étant donné un ensemble de points on cherche un ordre sur ces points (tri) un sous-ensemble de ces points (enveloppe convexe) ou des triplets formés par ces points (triangulation de Delaunay).Pour prendre ces décisions, l'algorithme combinatoire va se poser des questions géométriques élémentaires que l'on appelle prédicats, par exemple, comparaison de l'abscisse de deux points, orientation d'un triangle défini par trois points ou appartenance d'un point au cercle passant par trois autres points.