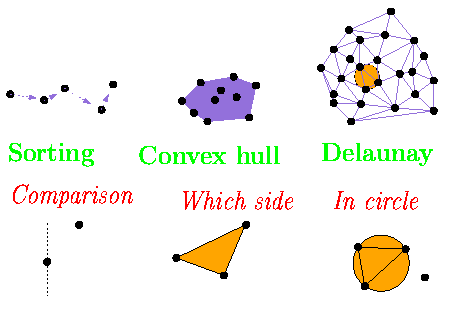
Combinatorics and predicates
Most algorithms are combinatorial, the computed information is of discrete nature, for example, given a set of points we are looking for an order among these points (sorting), a subset of the points (convex hull) or triples formed by these points (Delaunay triangulation).To take decisions, the combinatorial algorithm asks elementary geometric questions called predicates, for example, comparison of abscissae of two points, orientation of a triangle defined by three points or side of a point with respect to a circle through three other points.