Diagramme de Voronoï
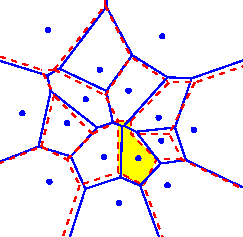
Dans le cas du diagramme de Voronoï bidimensionnel, on cherche à arrondir les sommets de Voronoï aux points d'une grille en conservant les propriétés intéressantes du diagramme, telles que la planarité du plongement et la convexité des cellules.Si on arrondit les sommets de Voronoï aux points de la grille les plus proches, il se peut que ces propriétés soient perdues. C'est ce qui arrive dans l'exemple à gauche, où le Voronoï exact (en bleu) est arrondi (en rouge) en créant une cellule non convexe (en jaune).
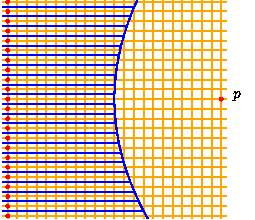
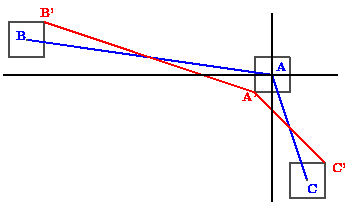
La figure à droite donne un exemple dans lequel il n'est pas possible d'arrondir le diagramme de Voronoï (bleu) sur la grille (orange) dans de bonnes conditions.