Voronoi diagrams
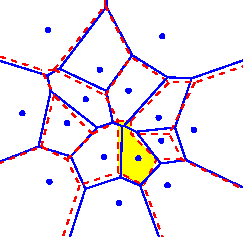
In the case of Voronoi diagrams in two dimensions, we need to round the Voronoi vertices on a regular grid while keeping interesting properties of Voronoi diagrams such as planarity or convexity of the cells.If the vertices are rounded to the nearest grid points, such properties may be lost. It happens in fact in the example on the left, where the Voronoi diagram (in blue) is rounded (in red) making a cell (the yellow one) non convex.
Figure on the right shows an example where it is impossible to round the Voronoi (blue) diagram on the (orange) grid with good properties.