Un problème de précision

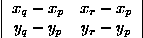
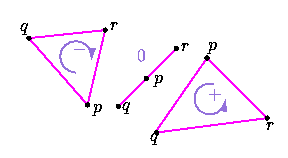
Un exemple : l'orientation d'un triangle Trois points p,q,r peuvent définir un triangle orienté dans le sens direct, indirect ou peuvent être alignés. Ces trois cas correspondent à une valeur positive, négative ou nulle du déterminant :

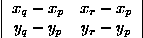
Le calcul arrondi fait des erreurs Supposons que l'on dispose d'une machine très peu précise qui ne calcule qu'avec deux chiffres significatifs en base 10 (les vraies machines calculent de la même façon mais en base 2 avec en général 24 ou 53 chiffres). 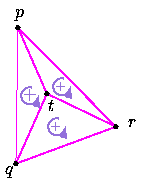Prenons comme coordonnées pour les points p = (-94,0) q = (92,68) r = (400,180) La vraie valeur du déterminant est (92+94)*180-(400+94)*68=186*180-494*68=33480-33592=-112 La valeur calculée par notre machine est (92+94)*180-(400+94)*68=190*180-490*68=34000-33000=+1000 Le triangle pqr est en réalité indirect, mais le calcul arrondi se trompe. Ces erreurs peuvent entrainer des problèmes d'incohérence. Mathématiquement, si les triangles pqt, qrt et rpt sont direct alors pqr est également direct. Ce genre de théorème mathématiquement juste peut se trouver invalidé par des tests en machine à cause des erreurs d'arrondis. L'algorithme qui se basait sur ce théorème risque alors de rentrer dans un boucle infinie ou de planter.

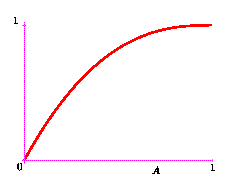
Le calcul arrondi ne fait pas tant d'erreur que ça On l'a vu le calcul arrondi fait des erreurs, mais heureusement, pas tant que ça. Une erreur ne peut se produire que si la valeur obtenue par le calcul arrondi est assez petite. La courbe ci contre donne la probabilité que la valeur du determinant soit plus petite qu'une valeur donnée A si les points p, q et r sont pris au hasard uniformément dans un cercle. On peut utiliser ce résultat pour montrer que si on calcule avec l'arithmétique habituelle en double précision, le test sera faux avec une probabilité inférieure à

On peut calculer exactement

Quand la valeur arrondie calculée par l'arithmétique arrondie est suffisamment grande pour que l'on puisse certifier son signe, on peut utiliser le résultat du test flottant.

Si la valeur calculée est trop proche de zéro il faut faire autre chose. On utilise l'arithmétique arrondie pour filtrer les cas difficiles.

Dans ces cas difficiles, il faut utiliser une méthode de calcul exacte. Soit à l'aide d'une bibliothèque de calcul en grande précision, soit à l'aide d'une méthode spécifiquement géométrique.

Filtres arithmétiques

Cela veut dire qu'il faut accompagner le calcul de notre déterminant d'un calcul d'erreur rigoureux permettant de certifier vraiment le signe calculé. Selon les cas on pourra parler de

• Filtre statique. Les données initiales sont supposées être bornées par une valeur connue à l'avance. Un calcul d'erreur dans le cas le pire est effectué avant la compilation.
• Filtre dynamique. L'erreur est calculée pas à pas, typiquement en utilisant de l'arithmétique d'intervalle, où l'on maintient des bornes supérieures et inférieures sur tout les résultats intermédiaires. On filtre ainsi plus de cas, mais cela coute plus cher à chaque fois.
• Filtre semi-statique. Entre ces deux méthodes, diverses solutions intermédiaires osnt envisageables.

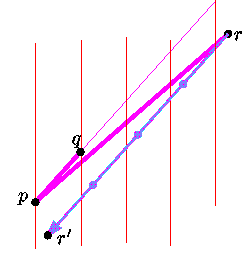
Calcul exact «géométrique» Nous avons développé une telle méthode: pour connaître l'orientation du triangle pqr dans un cas difficile où on translate r un nombre entier de fois du vecteur qp en un point r' tel que Cette translation ne change pas l'orientation du triangle, et le nouveau déterminant est plus facile à calculer. Pour en savoir plus

On peut se passer de calculer exactement

De tels algorithmes remplacent généralement la cohérence intrinsèque due aux théorèmes mathématiques par une vérification et un maintien explicite de cette cohérence.

Pour en savoir plus

Un exposé d'introduction.

Last modified: Mon Aug 28 10:31:13 MET DST 2000

Olivier Devillers

Thèmes