For instance: computing the orientation of a triangle
Three points p,q,r define a clockwise, counter-clockwise triangle, or may be aligned. These three cases correspond to a positive, negative, or null value of the following determinant:
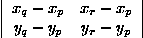
If a numerical result is sought, these imprecisions are usually acceptable. If a logical decision has to be taken based on this result (for example based on the sign of the result), the decision will be right in most cases but may be wrong (if the value is close to zero, its sign is not guaranteed to be correct). The consequences of taking a wrong decision can be fatal to the algorithm.
For instance: computing the orientation of a triangleThree points p,q,r define a clockwise, counter-clockwise triangle, or may be aligned. These three cases correspond to a positive, negative, or null value of the following determinant:
|
|
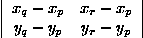
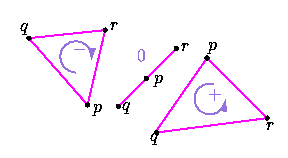
Rounding off leads to the wrong orientationSuppose our computer computes in base 10, but only keeps the two most significant digits. We call this fixed precision computation.Let us take three points:
Triangle pqr is oriented clockwise, but our computer is lead to the opposite conclusion because it rounds off the computation. Errors such as this can lead to inconsistencies. Mathematically, if triangles pqt, qrt et rpt are oriented counter-clockwise, then triangle pqr is also oriented counter-clockwise. This kind of mathematical theorem can be invalidated by fixed precision computations, because of round-off errors. |
 |
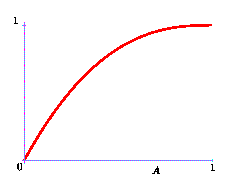
Floating point computation is not that badAs we have seen, fixed precision computation can lead to inconsistent results. Fortunately, it does not happen too often. Specifically, it only happens when the result of a fixed precision computation is small enough.Shown on the right is a curve that gives the probability that the computed value of the determinant is smaller that A, for three points p,q,r picked uniformly at random in a unit circle.
This kind of result can be used to show that, when we compute the
orientation as above on a computer that uses standard double
precision, the answer will be incorrect with a probability smaller
that |
 |
When the rounded computed value is large enough to certify its sign, the rounded result can be used.
If the computed value is to close from zero, something else is needed. The rounded arithmetic is used to filter difficult cases.
In these difficult cases, an exact computation must be done, either using an exact arithmetic library, either through a geometric method.
Thus, the computation of our determinant must be done with a rigorous error computation to allow to certify the computed sign. Depending on the error computation method, we will speak about
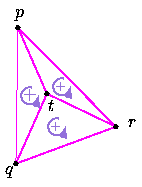
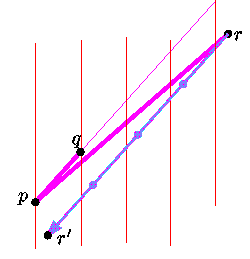
Geometrical exact computationsWe developed such a method: in order to know the orientation of a triangle pqr in the difficult case when
we translate r by an integral multiple of qp to yield a
point r' such that
This translation does not change the orientation and the new
determinant is easier to compute.
|
 |
In general, such algorithms replace the intrinsic consistency implied by the underlying mathematics by explicitly checking and maintaining this consistency.
Un survey talk.
| Last modified: Mon Aug 28 10:31:39 MET DST 2000 | Olivier Devillers | Topics |
|
