Estimation paramétrique multi-modèle robuste: une introduction
A. C. Belon
Nous revisitons ici une méthode d'estimation paramétrique utilisées en vision par ordinateur: une variante de la méthode de Kanatani, présentée ici comme un simple problème d'optimisation.
On utilise :
- des équations de mesures et des contraintes sur les paramètres non linéaires,
- une stratégie d'estimation robuste en présence de mesures erronnées,
- la mise en concurrence de plusieurs modèles au sein d'une hiérarchie.
Nous allons fournir ici une présentation résumée de
[1,2] peut-être plus
accessible et en discuter les implications. Cette méthode utilise un
algorithme de projection basé sur des décompositions de Cholesky
permettant une résolution numérique locale stable et efficace de
l'ensemble des équations de contraintes non linéaires. Un module
d'estimation robuste de paramètres appartenant à une hiériarchie de
modèles y a été intégré à partir de cet algorithme initial.
Les principaux problèmes rencontrés lors de l'estimation de paramètres viennent du fait que l'on doit prendre en compte différents aspects.
- L'estimation est non linéaire.
En effet, les objets géométriques et cinématiques ne sont pas représentés par un simple vecteur dans un espace euclidien.
Pour paramétriser un objet, il faut donc :
- utiliser différentes représentations et en changer au cours du processus d'estimation,
- ou introduire des contraintes dans la représentation, en utilisant des équations implicites, ce que nous faisons ici.
- Les mesures sont approximatives et contiennent des artefacts.
Les mesures obtenues sont souvent à la fois :
- approximatives (bruitées, pas toujours précises,...),
- elles contiennent des artefacts (outliers = mesures erronées, données aberrantes,...),
- ou contiennent un mélange d'objets différents (inliers = plusieurs groupes de mesures sont mélangés et doivent être distingués).
- La singularité de certaines données.
Un ensemble de données peut être singulier du fait que :
- le paramètre n'est pas défini dans une situation donnée,
- l'ensemble des données ne permet pas d'obtenir une estimation valable (par exemple, il n'est pas possible d'estimer un plan si tous les points donnés sont colinéaires).
On veut donc pouvoir détecter ces singularités afin d'estimer un modèle plus spécifique.
La recherche d'un modèle minimal est aussi recommandée car, moins il y a de paramètres à estimer, plus le nombre de mesures requises est faible et plus l'estimation est numériquement robuste.
On veut aborder le problème de l'estimation non linéaire en utilisant un critère de minimisation.
Il apparaît qu'une méthode simple mais spécifique, basée sur une spécification des paramètres physiques introduits dans le processus peut être plus efficace que des algorithmes de minimisation sophistiqués.
L'idée principale est de représenter l'objet paramétré par un vecteur des paramètres dont la variation est considérée étape par étape, ce qui est une stratégie appropriée pour des estimations locales, des adaptations à des variations d'échelle limitée à une valeur par défaut, une estimation interactive où l'estimation initiale donnée par l'utilisateur est à redéfinir, des traitements de suivi, ...
Plus précisément, on propose qu'au niveau de la spécification, chaque valeur numérique du paramètre à estimer
(i) soit bornée i.e. 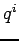 et
(ii) ait une précision finie
et
(ii) ait une précision finie
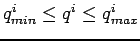 i.e.
i.e.
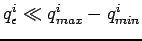
A côté de ces spécifications, on va associer à un tel paramètre ``physique'' :
(iii) une valeur par défaut
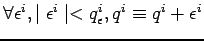 plus un
plus un
(iv) nom et une
(v) unité physique(seconde, pixel, ...).
On considère le problème ``simple'' d'estimer une quantité statique 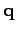 d'un ensemble de
d'un ensemble de 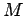 mesures
mesures 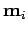 .
.
Figure 1:
Estimation d'un paramètre.
|
Plus précisément, on veut estimer une quantité vectorielle réelle à 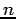 dimensions, soit un paramètre
dimensions, soit un paramètre
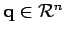 , étant donnés :
, étant donnés :
de telle sorte que les mesures approximatives sont corrigées par l'algorithme comme schématisé ici:
Figure 2:
Description du problème d'estimation.
|
La notion de données ``approximatives'' est formalisée en utilisant les semi-distances quadratiques :
pour
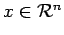 et
et
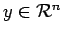 où Q est une matrice symétrique semi-définie positive. On l'appelle matrice d'information quadratique.
où Q est une matrice symétrique semi-définie positive. On l'appelle matrice d'information quadratique.
Si aucune estimation initiale n'est disponible, on peut simplement écrire
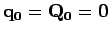 .
.
On peut formaliser le problème en tant que problème d'optimisation, c'est-à-dire estimer le paramètre
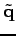 et les mesures
et les mesures
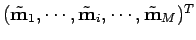 qui :
qui :
- minimisent la somme des distances définies :
- étant données les différentes équations :
De manière équivalente, le problème d'estimation peut être formulé comme un critère composé de multiplicateurs de Lagrange
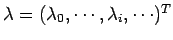 :
:
![\begin{displaymath}
\mbox{min}_{(\tilde {\bf q}, \tilde{\bf m}_1, \cdots, \tilde...
...mbda}_i^T \, {\bf c}_i(\tilde{\bf q}, \tilde{\bf m}_i) \right]
\end{displaymath}](synthese-img32.gif) |
(1) |
tandis que, dans le cas optimal
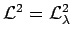 peut toujours être écrit, pour une matrice
peut toujours être écrit, pour une matrice 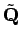 donnée :
donnée :
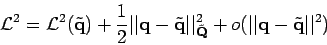 |
(2) |
Dans cette dernière équation, on ne définit pas seulement l'estimation du paramètre 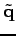 , mais aussi une distance quadratique du paramètre estimé paramétré par
, mais aussi une distance quadratique du paramètre estimé paramétré par 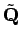 .
Cela permet d'évaluer la précision de l'estimation comme une distance quadratique.
.
Cela permet d'évaluer la précision de l'estimation comme une distance quadratique.
La méthode est assez directe bien qu'un peu compliquée :
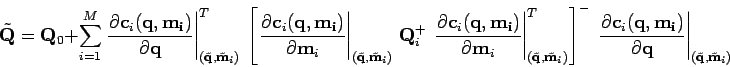 |
(3) |
où les notations 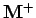 et
et 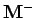 sont définies dans la section suivante.
sont définies dans la section suivante.
Le problème d'estimation de 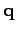 a
a 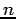 inconnues et
inconnues et 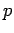 équations. Il y a donc
équations. Il y a donc 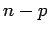 degrés de liberté.
degrés de liberté.
De plus, pour chaque mesure 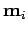 , il y a
, il y a 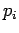 équations de contrainte donc chaque mesure du biais
équations de contrainte donc chaque mesure du biais
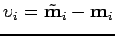 a
a 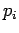 degrés de liberté.
degrés de liberté.
Une valeur normalisée du critère est donc :
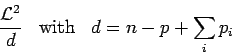 |
(4) |
où on a divisé par le nombre total de degrés de liberté.
Cette façon de définir l'estimation de paramètres vient du fait que :
- l'estimation de paramètres est performante même s'il y a trop (l'information est redondante) ou trop peu (le paramètre n'est que partiellement observable) de mesures,
- on peut combiner des mesures de géométrie ou de dynamique différentes, en utilisant les distances normalisées.
Puisque nous devons minimiser ce critère en respectant à la fois les estimations de paramètres et de mesures, le problème précédent peut être réécrit en utilisant les notations précédentes :
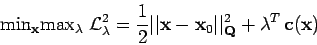 |
(5) |
avec
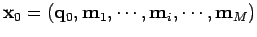 et
et
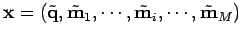 ; ainsi
; ainsi
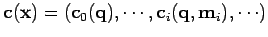 si on suppose que ces équations sont deux fois différentiables, puisque
si on suppose que ces équations sont deux fois différentiables, puisque
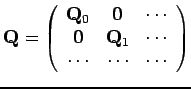 est une matrice diagonale.
est une matrice diagonale.
Ainsi, le problème est un simple problème de projection, i.e. le critère donné signifie qu'on veut trouver la quantité 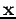 (i) la plus proche de
(i) la plus proche de 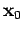 pour la distance quadratique paramétrisée par
pour la distance quadratique paramétrisée par 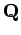 et (ii) dans l'ensemble
et (ii) dans l'ensemble 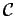 défini par
défini par
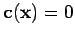 , comme schématisé dans la figure suivante :
, comme schématisé dans la figure suivante :
Figure 3:
L'estimation non linéaire en tant que problème de projection.
|
Ce problème a une solution unique si 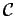 est un ensemble convexe ou linéaire et, on a une solution locale si
est un ensemble convexe ou linéaire et, on a une solution locale si 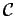 est, en quelque sorte, régulier, par exemple si la fonction
est, en quelque sorte, régulier, par exemple si la fonction
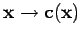 est deux fois différentiable avec des dérivées du second ordre finies dans un voisinage de
est deux fois différentiable avec des dérivées du second ordre finies dans un voisinage de 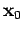 contenant la projection.
contenant la projection.
On considère l'approximation linéaire des équations non linéaires autour d'un point
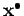 :
:
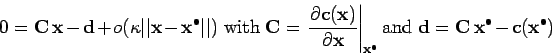 |
(6) |
où 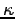 représente l'amplitude de la dérivée au second ordre de
représente l'amplitude de la dérivée au second ordre de
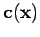 , associée à l'équation normale du critère en
, associée à l'équation normale du critère en
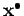 :
:
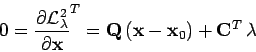 |
(7) |
On obtient un algorithme effectif permettant de calculer 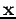 en tant que solution par itération du système linéaire approximatif :
en tant que solution par itération du système linéaire approximatif :
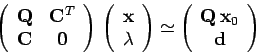 |
(8) |
On introduit quelques améliorations à cette méthode:
(a) utiliser des quantités partiellement définies,
(b) travailler avec des ensembles d'équations redondants ou singuliers,
(c) permettre, dans certains cas, la convergence de la méthode vers une valeur, pas nécessairement optimale mais, au moins, une estimation très réaliste.
La décomposition de Cholesky, ou en racines carrées, d'une matrice 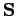 symétrique définie positive est un produit de matrices tel que
symétrique définie positive est un produit de matrices tel que
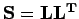 , où
, où 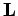 est une matrice triangulaire inférieure
On définit deux généralisations de la décomposition standard, dans le cas où la matrice n'est pas définie positive :
est une matrice triangulaire inférieure
On définit deux généralisations de la décomposition standard, dans le cas où la matrice n'est pas définie positive :
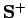 La décomposition en racines carrées ``la plus proche''.
La décomposition en racines carrées ``la plus proche''.- Il s'agit ici de la décomposition en racines carrées d'une matrice
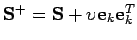 pour un
pour un 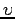 minimal.
minimal.
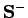 La décomposition en racines carrées ``réduite''.
La décomposition en racines carrées ``réduite''.- C'est la décomposition en racines carrées de la sous-matrice de
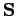 pour laquelle les lignes et les colonnes dont les éléments diagonaux sont petits, sont supprimés.
pour laquelle les lignes et les colonnes dont les éléments diagonaux sont petits, sont supprimés.
L'équation (7) nous donne :
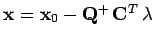 et, en considérant l'équation (6) en
et, en considérant l'équation (6) en 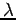 :
:
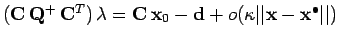 ,
,
on obtient la forme explicite :
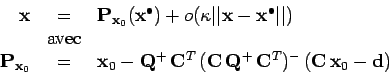 |
(9) |
On peut alors estimer l'erreur au premier ordre :
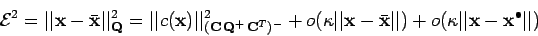 |
(10) |
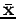 étant une estimation non biaisée de
étant une estimation non biaisée de 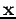 , i.e.
, i.e.
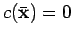 .
.
Dans le cas où on obtient la convergence, on peut calculer les séries
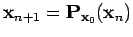 .
Pour éviter que l'estimation devienne instable, on propose d'utiliser l'algorithme :
.
Pour éviter que l'estimation devienne instable, on propose d'utiliser l'algorithme :
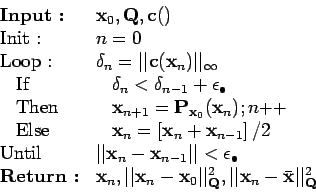 |
(11) |
qui permet de trouver un point proche de l'évaluation précédente. On voit, en effet, qu'il s'agit de calculer
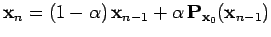 pour
pour
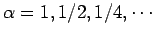 .
.
A l'entrée :
- une estimation initiale et un ensemble de mesures :
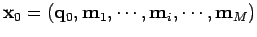 ,
,
- leur matrice d'information quadratique :
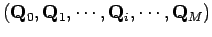 ,
,
- les équations de mesure et celles du paramètre :
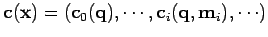 ,
avec
,
avec
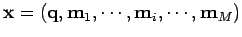 .
.
En sortie :
- un paramètre estimé et les mesures corrigées :
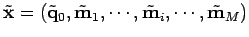 ,
,
- la matrice d'information quadratique
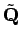 en fonction du paramètre estimé,
en fonction du paramètre estimé,
- l'erreur résiduelle
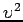 sur l'estimation,
sur l'estimation,
- la distance normalisée
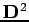 à partir de l'estimation d'origine.
à partir de l'estimation d'origine.
On implémente une méthode d'estimation aléatoire. On sélectionne aléatoirement un ensemble de mesures, en espérant qu'une d'entre elles, au moins, ne contient pas d'outlier. On détectera le ``bon'' échantillon du fait que son estimation semble la plus cohérente.
- On sélectionne un nombre minimal de mesures
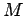 , telles que
, telles que
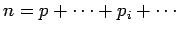 sans information initiale, i.e.
sans information initiale, i.e. 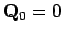 .
Cela suppose
.
Cela suppose
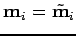 .
En résolvant le problème de projection, on obtient une estimation
.
En résolvant le problème de projection, on obtient une estimation 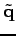 du paramètre, compatible avec cet ensemble de mesures.
On peut estimer la probabilité d'avoir sélectionné un ensemble correct de mesures en fonction de
du paramètre, compatible avec cet ensemble de mesures.
On peut estimer la probabilité d'avoir sélectionné un ensemble correct de mesures en fonction de 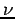 , pourcentage de mesures valides et de
, pourcentage de mesures valides et de 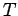 , le nombre d'échantillonnages :
, le nombre d'échantillonnages :
![\begin{displaymath}
P = \left[1 - \left[ 1 - \left( 1 - \frac{\nu}{100} \right)^{M} \right]^{T} \right]
\end{displaymath}](synthese-img87.gif) |
(12) |
- Avant cela, on calcule, pour chaque mesure, un indicateur de sa cohérence par rapport au paramètre estimé. On peut facilement se servir de l'erreur quadratique normalisée pour la ième mesure :
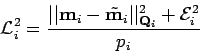 |
(13) |
- Pour estimer la validité du
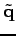 trouvé, les stratégies utilisées sont :
trouvé, les stratégies utilisées sont :
- soit trouver un nombre suffisant de ``bonnes'' mesures en comptant le pourcentage de mesures
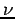 dont l'erreur est au-dessous d'un seuil fixé.
dont l'erreur est au-dessous d'un seuil fixé.
- soit trouver une erreur suffisamment petite en considérant l'erreur maximale des
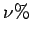 premières mesures qui ont la plus petite erreur.
premières mesures qui ont la plus petite erreur.
Dans ces deux cas, on doit :
- (i)
- choisir un nombre fixé
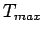 d'itérations et on prend la meilleure mesure.
d'itérations et on prend la meilleure mesure.
- (ii)
- réitérer jusqu'à obtenir une estimation valable.
Les méthodes robustes permettent d'éliminer facilement les outliers mais cela ne marche pas s'il y a plusieurs ensembles d'inliers, c'est-à-dire si la distribution est multi-modèles.
On suppose que si l'on a une distribution multi-modèles et une estimation qui combine plus d'une distribution ou qui inclut des outliers, l'histogramme d'erreur sera plus large autour de zéro tandis que, pour un ensemble unique d'inliers, l'histogramme sera plus reserré autour de zéro.
Figure 4:
La forme de la distribution de l'erreur en présence d'outliers.
|
Une telle distribution se caractérise par :
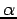 , l'amplitude de la distribution en zéro,
, l'amplitude de la distribution en zéro,
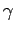 , la convexité de la distribution en zéro,
, la convexité de la distribution en zéro,
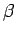 , le biais introduit par les outliers en zéro.
, le biais introduit par les outliers en zéro.
On veut maximiser à la fois 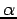 et
et 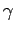 .
.
La validité du modèle peut être définie par :
![\begin{displaymath}
{\cal R} = \frac{1}{M} \, \left[ \mu_0 - 2 \, \frac{\mu_1}{{\cal L}^2_\bullet} \right] < 1
\end{displaymath}](synthese-img95.gif) |
(14) |
Il n'y a pas de solution générale pour savoir quand arrêter le processus.
Voici différentes stratégies :
- Parallelisation.
- On fait tourner le process avec une priorité qui décroît avec le temps. On fait en sorte d'avoir rapidement une estimation plausible et on continue s'il reste du temps.
- Interaction de l'utilisateur.
- A chaque nouvelle solution trouvée, celle-ci peut être présentée à l'utilisateur qui peut l'accepter ou/et continue le process.
- Seuillage automatique
- On peut utiliser la meilleure courbe de validité estimée pour déterminer automatiquement un seuil.
- (i)
- soit on stoppe quand il n'y a plus d'amélioration,
- (ii)
- soit on détecte un saut dans la courbe qui dénote un ensemble de bonnes mesures.
Finalement, on affine l'estimation de paramètres sur les mesures dont l'erreur est au-dessous du seuil, en reprenant la minimisation de 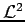 .
.
Minimiser le critère non linéaire ne suffit pas à obtenir une bonne estimation d'un paramètre :
- Estimer un paramètre ne signifie pas seulement calculer une valeur numérique mais choisir quel modèle correspond le mieux aux données.
- Puisque l'on trouve seulement une estimation locale du paramètre, la condition initiale est déterminante car le processus de minimisation peut ne pas converger.
Pour faire face à ces deux problèmes, on utilise un ensemble de modèles pour effectuer l'estimation de paramètres:
- Chaque problème d'estimation doit avoir un modèle nul comme référence (modèle avec le plus de contraintes).
- Chaque modèle est une généralisation d'autres modèles (ses parents) en enlevant ou remplaçant certaines contraintes.
Il y a aussi un modèle général sans équation (et sans intérêt!).
Figure 5:
Représenter une hiérarchie de modèles.
|
On considère que :
- pour tous les modèles, on doit estimer un paramètre commun
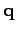 avec les mêmes équations de mesure
avec les mêmes équations de mesure
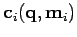 ,
,
- deux modèles diffèrent par leurs contraintes
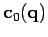 sur le paramètre, i.e. par le nombre
sur le paramètre, i.e. par le nombre 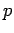 d'équations.
d'équations.
On a des équations entre le paramètre estimé 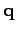 d'un modèle plus spécifique
d'un modèle plus spécifique 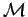 et le paramètre estimé
et le paramètre estimé 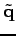 d'un modèle plus général
d'un modèle plus général
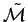 .
.
Un modèle plus général est choisi par rapport à un modèle plus spécifique si et seulement si le coût décroît selon un facteur
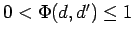 .
.
Afin d'implémenter une telle méthode en effectuant une estimation robuste, on suppose que :
(i) Etant donné un modèle valide (estimé sans outlier) pour un ensemble de mesures minimal, un modèle plus général qui requiert plus de mesures dans son ensemble minimal, peut toujours considérer les mesures de ses parents comme non outliers parce qu'elles vérifient aussi un sous-ensemble des équations de modèles avec lesquelles elles sont cohérentes.
(ii) Etant donné un modèle valide et une généralisation de celui-ci, des mesures additionnelles pour estimer le modèle général doivent être en dehors de l'ensemble des mesures appliquées au modèle le plus simple.
Ceci restreint le nombre de mesures et augmente la chance de sélectionner aléatoirement une bonne estimation.
Cela peut éviter de sélectionner des configurations singulières de points pour un modèle donné.
Afin d'implémenter ces idées :
- L''état'' d'un modèle est représenté par :
(i) le paramètre estimé 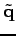 et sa précision relative
et sa précision relative 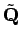 ,
,
(ii) les index des points échantillonnés pour estimer l'état,
(iii) les index des points non cohérents, i.e. des outliers pour ce modèle,
- tandis que le ``modèle'' est spécifié par :
(i) son nom,
(ii) ses contraintes et coût intrinsèque,
(iii) une liste d' ``alternatives'' i.e. des modèles moins spécifiques avec moins de contraintes,
(iv) leur facteur de coût relatif 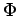 ,
,
(v) une liste de ``modèles'' qui sont parents de ceux-ci.
En utilisant cette structure de données, les idées précédentes sont implémentées par l'algorithme suivant :
- Initialisation
-
Prendre le modèle nul avec une valeur du paramètre
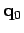 initiale fournie par l'utilisateur, dans une liste candidate.
initiale fournie par l'utilisateur, dans une liste candidate.
- Iteration
-
Pour chaque modèle de la liste :
- sélectionner aléatoirement un ensemble de mesures ``additionnelles'' dans l'ensemble de points non cohérents avec le modèle parent (s'il y en a un),
- estimer :
- le paramètre du modèle en utilisant le paramètre du modèle parent comme valeur initiale
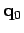 , en résolvant le problème de projection et en utilisant l'algorithme (11),
, en résolvant le problème de projection et en utilisant l'algorithme (11),
- la cohérence de chaque mesure, en résolvant le problème de projection et en utilisant l'algorithme (11),
- l'efficacité du modèle, comme on l'a décrit dans (14).
- Si ce modèle est plus valable que le précédent, le paramètre estimé pour ce modèle :
- remplace les estimations faites auparavant pour ce modèle,
- puis:
- on seuille l'ensemble des outliers, comme illustré dans la Fig. 4 en tenant compte des discussions précédentes,
- on affine l'estimation du paramètre du modèle, en appliquant l'algorithme (11) au projecteur,
- on répéte les étapes 1 et 2, afin de stabiliser l'estimation,
- on évalue son coût, à partir de (4).
- Si le coût est inférieur à celui du parent, ses alternatives sont introduites dans la liste candidate.
- le modèle est enlevé de la liste candidate.
- Sinon on répète l'itération en sélectionnant aléatoirement un modèle de la liste candidate.
- Fin et Sortie
-
Le modèle, dont le coût minimal appartient à un seuil donné, est choisi comme modèle le ``meilleur''.
- 1
-
T. Vieville, D. Lingrand, and F. Gaspard.
Implementing a variant of the Kanatani's estimation method.
RR 4050, INRIA, Nov. 2000.
- 2
-
T. Vieville, D. Lingrand, and F. Gaspard.
Implementing a multi-model estimation method.
The International Journal of Computer Vision, 44(1), 2001.
Thierry Vieville
2002-09-19
![]() et
(ii) ait une précision finie
et
(ii) ait une précision finie
![]() i.e.
i.e.
![]()
![]() plus un
plus un
![]() d'un ensemble de
d'un ensemble de ![]() mesures
mesures ![]() .
.
![]() dimensions, soit un paramètre
dimensions, soit un paramètre
![]() , étant donnés :
, étant donnés :
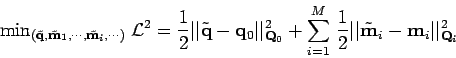
![]() :
:
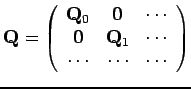 est une matrice diagonale.
est une matrice diagonale.
![]() (i) la plus proche de
(i) la plus proche de ![]() pour la distance quadratique paramétrisée par
pour la distance quadratique paramétrisée par ![]() et (ii) dans l'ensemble
et (ii) dans l'ensemble ![]() défini par
défini par
![]() , comme schématisé dans la figure suivante :
, comme schématisé dans la figure suivante :
![]() est un ensemble convexe ou linéaire et, on a une solution locale si
est un ensemble convexe ou linéaire et, on a une solution locale si ![]() est, en quelque sorte, régulier, par exemple si la fonction
est, en quelque sorte, régulier, par exemple si la fonction
![]() est deux fois différentiable avec des dérivées du second ordre finies dans un voisinage de
est deux fois différentiable avec des dérivées du second ordre finies dans un voisinage de ![]() contenant la projection.
contenant la projection.
![]() représente l'amplitude de la dérivée au second ordre de
représente l'amplitude de la dérivée au second ordre de
![]() , associée à l'équation normale du critère en
, associée à l'équation normale du critère en
![]() :
:
![]() en tant que solution par itération du système linéaire approximatif :
en tant que solution par itération du système linéaire approximatif :
![]() étant une estimation non biaisée de
étant une estimation non biaisée de ![]() , i.e.
, i.e.
![]() .
.
![]() pour
pour
![]() .
.
![]() et
et ![]() .
.