Selected publications:

Optimizing Voronoi Diagrams for Polygonal Finite Element Computations
Daniel Sieger, Pierre Alliez and Mario Botsch
Proceedings of the 19th International Meshing Roundtable, 2010.

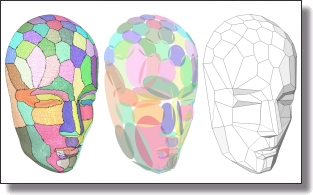
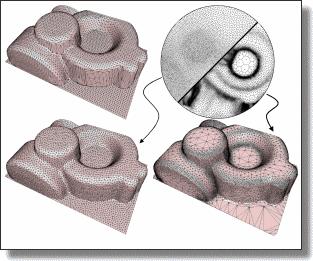
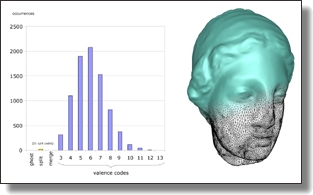
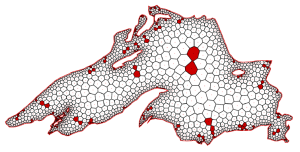
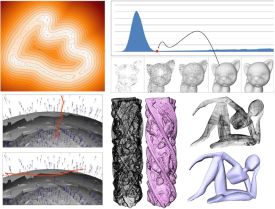
Abstract: We present a 2D mesh improvement technique that optimizes Voronoi diagrams for their use in polygonal nite element computations. Starting from a centroidal Voronoi tessellation of the simulation domain we optimize the mesh by minimizing a carefully designed energy functional that effectively removes the major reason for numerical instabilities: short edges in the Voronoi diagram. We evaluate our method on a 2D Poisson problem and demonstrate that our simple but e ective optimization achieves a significant improvement of the stiffness matrix condition number.

Signing the Unsigned: Robust Surface Reconstruction from Raw Pointsets
Patrick Mullen, Fernando de Goes, Mathieu Desbrun, David Cohen-Steiner and Pierre Alliez.
EUROGRAPHICS Symposium on Geometry Processing 2010.

Abstract: We propose a modular framework for robust 3D reconstruction from unorganized, unoriented, noisy, and outlierridden geometric data. We gain robustness and scalability over previous methods through an unsigned distance approximation to the input data followed by a global stochastic signing of the function. An isosurface reconstruction is finally deduced via a sparse linear solve. We show with experiments on large, raw, geometric datasets that this approach is scalable while robust to noise, outliers, and holes. The modularity of our approach facilitates customization of the pipeline components to exploit specific idiosyncracies of datasets, while the simplicity of each component leads to a straightforward implementation.
Interleaving Delaunay Refinement and Optimization for Practical Isotropic Tetrahedron Mesh Generation
Jane Tournois, Camille Wormser, Pierre Alliez and Mathieu Desbrun
ACM Transactions on Graphics (SIGGRAPH), 28(3), 2009.

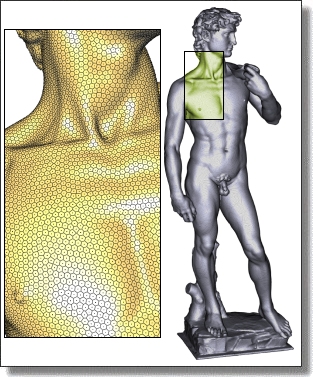
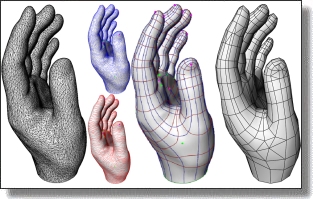
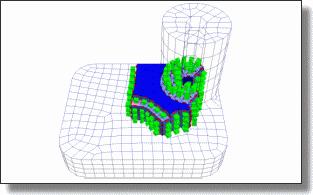
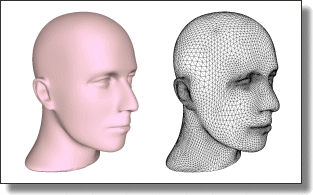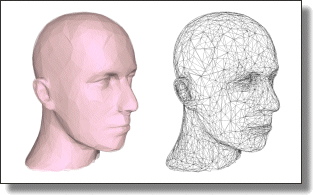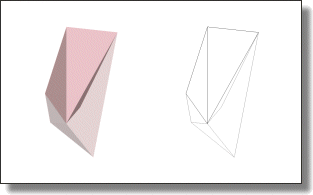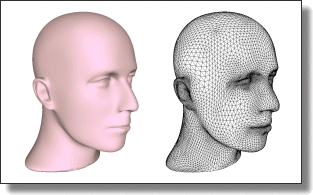
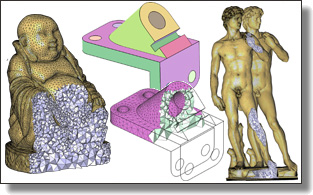
Abstract: We present a practical approach to isotropic tetrahedral meshing of 3D domains bounded by piecewise smooth surfaces. Building upon recent theoretical and practical advances, our algorithm interleaves Delaunay refinement and mesh optimization to generate quality meshes that satisfy a set of user-defined criteria. This interleaving is shown to be more conservative in number of Steiner point insertions than refinement alone, and to produce higher quality meshes than optimization alone. A careful treatment of boundaries and their features is presented, offering a versatile framework for designing smoothly graded tetrahedral meshes.


Perturbing Slivers in 3D Delaunay Meshes
Jane Tournois, Rahul Srinivasan and Pierre Alliez
International Meshing Roundtable 2009.

Abstract: Isotropic tetrahedron meshes generated by Delaunay triangulations are known to contain a majority of well-shaped tetrahedra, as well as spurious sliver tetrahedra. As the slivers hamper stability of numerical simulations we aim at removing them while keeping the triangulation Delaunay for simplicity. The solution which explicitly perturbs the slivers through random vertex relocation and Delaunay connectivity update is very effective but slow. In this paper we present a perturbation algorithm which favors deterministic over random perturbation. The added value is an improved efficiency and effectiveness. Our experimental study applies the proposed algorithm to meshes obtained by Delaunay refinement as well as to carefully optimized meshes.

Filtering Relocations on a Delaunay Triangulation
Pedro Machado, Jane Tournois, Pierre Alliez and Olivier Devillers
EUROGRAPHICS Symposium on Geometry Processing 2009.

Abstract: Updating a Delaunay triangulation when its vertices move is a bottleneck in several domains of application. Rebuilding the whole triangulation from scratch is surprisingly a very viable option compared to relocating the vertices. This can be explained by several recent advances in efficient construction of Delaunay triangulations. However, when all points move with a small magnitude, or when only a fraction of the vertices move, rebuilding is no longer the best option. This paper considers the problem of efficiently updating a Delaunay triangulation when its vertices are moving under small perturbations. The main contribution is a set of filters based upon the concept of vertex tolerances. Experiments show that filtering relocations is faster than rebuilding the whole triangulation from scratch under certain conditions.

 

CGAL - The Computational Geometry Algorithms Library
Pierre Alliez, Andreas Fabri, Efi Fogel.
SIGGRAPH 2008 course notes (pdf)

Spectral Conformal Parameterization (pdf)

Patrick Mullen, Yiying Tong, Pierre Alliez and Mathieu Desbrun.
Symposium on Geometry Processing, 2008.

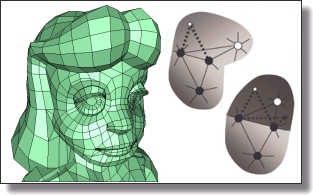
We present a spectral approach to automatically and efficiently obtain discrete free-boundary conformal parameterizations of triangle mesh patches, without the common artifacts due to positional constraints on vertices and without undue bias introduced by sampling irregularity. High-quality parameterizations are computed through a constrained minimization of a discrete weighted conformal energy by finding the largest eigenvalue/eigenvector of a generalized eigenvalue problem involving sparse, symmetric matrices. We demonstrate that this novel and robust approach improves on previous linear techniques both quantitatively and qualitatively.

 
Geometric Modeling Based on Polygonal Meshes.
Mario Botsch, Mark Pauly, Leif Kobbelt, Pierre Alliez, Bruno Levy, Stephan Bischoff, Christian Rössl.
Eurographics 2008 Course Notes.
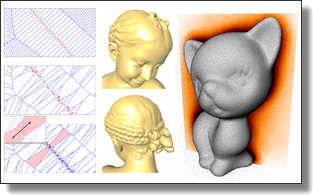
Voronoi-based Variational Reconstruction of Unoriented Point Sets
Pierre Alliez, David Cohen-Steiner, Yiying Tong, and Mathieu Desbrun. Symposium on Geometry Processing, 2007, pages 39-48. (best paper award)
Download slides (ppt format)


Abstract: We introduce an algorithm for reconstructing watertight surfaces from unoriented point sets. Using the Voronoi diagram of the input point set, we deduce a tensor field whose principal axes and eccentricities locally represent respectively the most likely direction of the normal to the surface, and the confidence in this direction estimation. An implicit function is then computed by solving a generalized eigenvalue problem such that its gradient is most aligned with the principal axes of the tensor field, providing a best-fitting isosurface reconstruction. Our approach possesses a number of distinguishing features. In particular, the implicit function optimization provides resilience to noise, adjustable fitting to the data, and controllable smoothness of the reconstructed surface. Finally, the use of simplicial meshes (possibly restricted to a thin crust around the input data) and (an)isotropic Laplace operators renders the numerical treatment simple and robust.
Geometric Modeling Based on Polygonal Meshes
Mario Botsch, Mark Pauly, Leif Kobbelt, Pierre Alliez, Bruno Levy, Stephan Bischoff and Christian Rössl.
SIGGRAPH 2007 Course Notes (award for the best revised course notes)
Interleaving Delaunay Refinement and Optimization for 2D Triangle Mesh Generation
Jane Tournois, Pierre Alliez and Olivier Devillers
16th International Meshing Roundtable

Abstract: We address the problem of generating 2D quality triangle meshes from a set of constraints provided as a planar straight line graph. The algorithm first computes a constrained Delaunay triangulation of the input set of constraints, then interleaves Delaunay refinement and optimization. The refinement stage inserts a subset of the Voronoi vertices and midpoints of constrained edges as Steiner points. The optimization stage optimizes the shape of the triangles through the Lloyd iteration applied to Steiner points both in 1D along constrained edges and in 2D after computing the bounded Voronoi diagram. Our experiments show that the proposed algorithm inserts fewer Steiner points than Delaunay refinement alone, and improves over the mesh quality.

 

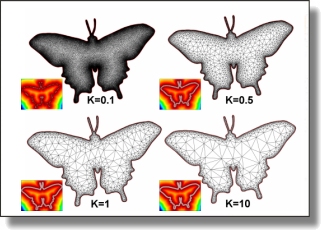
Mesh Sizing with Additively Weighted Voronoi Diagrams
Lakulish Antani, Christophe Delage and Pierre Alliez
16th International Meshin Roundtable

Abstract: We address the problem of generating mesh sizing functions from a set of points with specified sizing values. The sizing functions are shown to be maximal and K-Lipschitz, with arbitrary parameter K provided by the user. These properties allow generating low complexity meshes with adjustable gradation. After constructing an additively weighted Voronoi diagram, our algorithm provides fast and accurate answers to arbitrary point queries. We have implemented our mesh sizing technique as a sizing criterion for the 2D triangle meshing component from the CGAL library. We demonstrate the performance advantages of our technique through experimental results on various inputs.

 

 

Designing Quadrangulations with Discrete Harmonic Forms
Yiying Tong, Pierre Alliez, David Cohen-Steiner, and Mathieu Desbrun
ACM/EG Symposium on Geometry Processing 2006
Abstract: We introduce a framework for quadrangle meshing of discrete manifolds. Based on discrete differential forms, our method hinges on extending the discrete Laplacian operator (used extensively in modeling and animation) to allow for line singularities and singularities with fractional indices. When assembled into a singularity graph, these line singularities are shown to considerably increase the design flexibility of quad meshing. In particular, control over edge alignments and mesh sizing are unique features of our novel approach. Another appeal of our method is its robustness and scalability from a numerical viewpoint: we simply solve a sparse linear system to generate a pair of piecewise-smooth scalar fields whose isocontours form a pure quadrangle tiling, with no T-junctions.
Reconstruction with Voronoi Centered Radial Basis Functions
Marie Samozino, Marc Alexa, Pierre Alliez and Mariette Yvinec
ACM/EG Symposium on Geometry Processing 2006
We consider the problem of reconstructing a surface from scattered points sampled on a physical shape. The sampled shape is approximated as the zero level set of a function. This function is defined as a linear combination of compactly supported radial basis functions. We depart from previous work by using as centers of basis functions a set of points located on an estimate of the medial axis, instead of the input data points. Those centers are selected among the vertices of the Voronoi diagram of the sample data points. Being a Voronoi vertex, each center is associated with a maximal empty ball. We use the radius of this ball to adapt the support of each radial basis function. Our method can fit a user-defined budget of centers: The selected subset of Voronoi vertices is filtered using the notion of lambda medial axis, then clustered to fit the allocated budget.

Variational Tetrahedral Meshing
Pierre Alliez, David Cohen-Steiner, Mariette Yvinec and Mathieu Desbrun.
SIGGRAPH 2005.

Abstract: In this paper, a novel Delaunay-based variational approach to isotropic tetrahedral meshing is presented. To achieve both robustness and efficiency, we minimize a simple mesh-dependent energy through global updates of both vertex positions and connectivity. As this energy is known to be the L1 distance between an isotropic quadratic function and its linear interpolation on the mesh, our minimization procedure generates well-shaped tetrahedra. Mesh design is controlled through a gradation smoothness parameter and selection of the desired number of vertices. We provide the foundations of our approach by explaining both the underlying variational principle and its geometric interpretation. We demonstrate the quality of the resulting meshes through a series of examples.
Farthest Point Seeding for Efficient Placement of Streamlines
Abdelkrim Mebarki, Pierre Alliez and Olivier Devillers.
VISUALIZATION 2005

Abstract: We propose a novel algorithm for placement of streamlines from two-dimensional steady vector or direction fields. Our method consists of placing one streamline at a time by numerical integration starting at the furthest away from all previously placed streamlines. Such a farthest point seeding strategy leads to high quality placements by favoring long streamlines, while retaining uniformity with the increasing density. Our greedy approach generates placements of comparable quality with respect to the optimization approach from Turk and Banks, while being 200 times faster. Simplicity, robustness as well as efficiency is achieved through the use of a Delaunay triangulation to model the streamlines, address proximity queries and determine the biggest voids by exploiting the empty circle property. Our method handles variable density and extends to multiresolution.

Recent Advances in Remeshing of Surfaces
Pierre Alliez, Giuliana Ucelli, Craig Gotsman and
Marco Attene
Part of the state-of-the-art report of the AIM@SHAPE EU network

Abstract: Remeshing is a key component of many geometric lgorithms, including modeling, editing, animation and simulation. As such, the rapidly developing field of geometry processing has produced a profusion of new remeshing techniques over the past few years. In this paper we survey recent developments in remeshing of surfaces, focusing mainly on graphics applications. We classify the techniques into five categories based on their end goal: structured, compatible, high quality, feature and error-driven remeshing. We limit our description to the main ideas and intuition behind each technique, and a brief comparison between some of the techniques. We also list some open questions and directions for future research.

 

Periodic Global Parameterization
Nicolas Ray, Wan Chiu Li, Bruno Levy, Alla Sheffer and Pierre Alliez
To appear at Transactions on Graphics.

Abstract: We present a new globally smooth parameterization method for surfaces of arbitrary topology.Our method does not require any prior partition into charts nor any cutting. The chart layout (i.e., the topology of the base complex) and the parameterization emerge simultaneously from a global numerical optimization process. Given two orthogonal piecewise linear vector fields, our method computes two piecewise linear periodic functions, aligned with the input vector fields, by minimizing an objective function. The bivariate function they define is a smooth parameterization almost everywhere, except in the vicinity of the singular points of the vector field, where both the vector field and the derivatives of the parameterization vanish. Our method can construct quasi-isometric parameterizations at the expense of introducing additional singular points in non-developable regions where the curl of the input vector field is non-zero. We also propose a curvature-adapted parameterization method, that minimizes the curl and removes those additional singular points by adaptively scaling the parameterization. In addition, the same formalism is used to allow smoothing of the control vector fields. We demonstrate the versatility of our method by using it for quad-dominant remeshing and T-spline surface fitting. For both applications, the input vector fields are derived by estimating the principal directions of curvatures.

Model courtesy of the Digital Michelangelo Project, Stanford University

Variational Shape Approximation
David Cohen-Steiner, Pierre Alliez and Mathieu Desbrun
SIGGRAPH '2004.
Download PDF [11 MBytes]
Bibtex
Abstract: Achieving efficiency in mesh processing often demands that overly verbose 3D datasets be reduced to more concise, yet faithful representations. Despite numerous applications ranging from geometry compression to reverse engineering, concisely capturing the geometry of a surface remains a tedious task. In this paper, we present both theoretical and practical contributions that result in a novel and versatile framework for geometric approximation of surfaces. We depart from the usual strategy by casting shape approximation as a variational geometric partitioning problem. Using the concept of geometric proxies, we drive the distortion error down through repeated clustering of faces into best-fitting regions. Our approach is entirely discrete and error-driven, and does not require parameterization or local estimations of differential quantities. We also introduce a new metric based on normal deviation, and demonstrate its superior behavior at capturing anisotropy.

Note: two extensions of this algorithm have been proposed for non planar proxies. Check the following papers:

- Structure Recovery via Hybrid Variational Surface Approximation. Jianhua Wu, Leif Kobbelt. Computer Graphics Forum, Volume 24, Number 3, 2005, pp. 277 - 284 (Eurographics 2005 proceedings).

- Dong-Ming Yan, Yang Liu and Wenping Wang: Quadric Surface Extraction by Variational Shape Approximation, Geometric Modeling and Processing (GMP) 2006.


 

Recent Advances in Compression of 3D Meshes
Pierre Alliez and Craig Gotsman
Advances in Multiresolution for Geometric Modelling. N.A. Dodgson and M.S. Floater and M.A. Sabin. Springer-Verlag editors. ISBN 3-540-21462-3. Pages 3-26. 2005.

Download PDF [5 MBytes]
Download PPT Slides [10 MBytes]
Bibtex
Abstract: 3D meshes are widely used in graphic and simulation applications for approximating 3D objects. When representing complex shapes in a raw data format, meshes consume a large amount of space. Applications calling for compact storage and fast transmission of 3D meshes have motivated the multitude of algorithms developed to efficiently compress these datasets. In this paper we survey recent developments in compression of 3D surface meshes. We survey the main ideas and intuition behind techniques for single-rate and progressive mesh coding. Where possible, we discuss the theoretical results obtained for asymptotic behavior or optimality of the approach.We also list some open questions and directions for future research.




Isotropic Remeshing of Surfaces: a Local Parameterization Approach
Vitaly Surazhsky, Pierre Alliez and Craig Gotsman
Proceedings of 12th International Meshing Roundtable, September 2003.
Download PDF [20 MBytes]
Bibtex

Abstract:We present a method for isotropic remeshing of arbitrary genus surfaces. The method is based on a mesh adaptation process, namely, a sequence of local modifications performed on a copy of the original mesh, while referring to the original mesh geometry. The algorithm has three stages. In the first stage the required number or vertices are generated by iterative simplification or refinement. The second stage performs an initial vertex partition using an area-based relaxation method. The third stage achieves precise isotropic vertex sampling prescribed by a given density function on the mesh. We use a modification of Lloyd's relaxation method to construct a weighted centroidal Voronoi tessellation of the mesh. We apply these iterations locally on small patches of the mesh that are parameterized into the 2D plane. This allows us to handle arbitrary complex meshes with any genus and any number of boundaries. The efficiency and the accuracy of the remeshing process is achieved using a patch-wise parameterization technique.

 

Anisotropic Polygonal Remeshing
Pierre Alliez, David Cohen-Steiner, Olivier Devillers, Bruno Levy and Mathieu Desbrun. 
SIGGRAPH'2003.
Download PDF [20 MBytes]
Download PPT slides [30 MBytes]
Bibtex

Abstract:  In this paper, we propose a novel polygonal remeshing technique that exploits a key aspect of surfaces: the intrinsic anisotropy of natural or man-made geometry. In particular, we use curvature directions to drive the remeshing process, mimicking the lines that artists themselves would use when creating 3D models from scratch. After extracting and smoothing the curvature tensor field of an input genus-0 surface patch, lines of minimum and  maximum curvatures are used to determine appropriate edges for the remeshed version in anisotropic regions, while spherical regions are simply point-sampled since there is no natural direction of symmetry locally. As a result our technique generates polygon meshes mainly composed of quads in anisotropic regions, and of triangles in spherical regions. Our approach provides the flexibility to produce meshes ranging from isotropic to anisotropic, from coarse to dense, and from  uniform to curvature adapted.

Note: an improved version of this algorithm has been presented in: Direct Anisotropic Quad-Dominant Remeshing.
Martin Marinov, Leif Kobbelt.
Proc. Pacific Graphics, 207-216, 2004

 

Isotropic Surface Remeshing 
Pierre Alliez , Eric Colin de Verdiere, Olivier Devillers and Martin Isenburg 
Shape Modeling International 2003.
Download PDF [10 MBytes]
Download PPT slides [50 MBytes]
Bibtex

Abstract: This paper proposes a new method for isotropic remeshing of triangulated surface meshes. Given a triangulated surface mesh to be resampled and a user-specified density function defined over it, we first distribute the desired number of samples by generalizing error diffusion, commonly used in image halftoning, to work directly on mesh triangles and feature edges. We then use the resulting sampling as an initial configuration for building a weighted centroidal Voronoi tessellation in a conformal parameter space, where the specified density function is used for weighting. We finally create the mesh by lifting the corresponding constrained Delaunay triangulation from parameter space. A precise control over the sampling is obtained through a flexible design of the density function, the latter being possibly low-pass filtered to obtain a smoother gradation. We demonstrate the versatility of our approach through various remeshing examples.

 

 
Compressing Hexahedral Volume Meshes 
Martin Isenburg and Pierre Alliez
In PACIFIC GRAPHICS '2002 conference proceedings
Download PDF [5.1 MBytes]
Bibtex

Abstract: Unstructured hexahedral volume meshes are of particular interest for visualization and simulation applications. They allow regular tiling of the three-dimensional space and show good numerical behaviour in finite element computations. Beside such appealing properties, volume meshes take huge amount of space when stored in a raw format. In this paper we present a technique for encoding connectivity and geometry of unstructured hexahedral volume meshes. For connectivity compression, we extend the idea of coding with degrees as pioneered by Touma and Gotsman  to volume meshes. Hexahedral connectivity is coded as a sequence of edge degrees. This naturally exploits the regularity of typical hexahedral meshes. We achieve connectivity compression rates of around 1:5 bits per hexahedron that go down to 0:18 for regular meshes. For geometry compression, we perform simple parallelogram prediction on uniformly quantized vertices within the side of a hexahedron. At a quantization level of 16 bits the average geometry compression ratio is 3:7 on our test meshes.

 

Compressing Polygon Mesh Geometry with Parallelogram Prediction 
Martin Isenburg and Pierre Alliez
In VISUALIZATION  '2002 conference proceedings 
Download PDF [1 MByte]
Bibtex

Abstract: In this paper we present a generalization of the geometry coder by Touma and Gotsman to polygon meshes. We let the polygon information dictate where to apply their parallelogram predictor. Since polygons tend to be fairly planar and fairly convex, it is beneficial to make predictions within a polygon rather than across polygons. This, for example, avoids poor predictions due to a crease angle between polygons. Up to 90 percent of the vertices can be predicted this way. Our strategy improves geometry compression by 10 to 40 percent depending on (a) how polygonal the mesh is and (b) on the quality (planarity / convexity) of the polygons.

Near-Optimal Connectivity Encoding of 2-Manifold Polygon Meshes
Andrei Khodakovsky, Pierre Alliez, Mathieu Desbrun and Peter Schröder
Journal of the Graphical Models, 64(3-4).,2002 .
Download PDF [558 kBytes]
Bibtex

Abstract: Encoders for triangle mesh connectivity based on enumeration of vertex valences are among the best reported to date. They are both simple to implement and report the best compressed file sizes for a large corpus of test models. Additionally they have recently been shown to be near-optimal since they realize the Tutte entropy bound for all planar triangulations. In this paper more...

 
Angle-Analyzer: A Triangle-Quad Mesh Codec
Haeyoung Lee, Pierre Alliez and Mathieu Desbrun
In EUROGRAPHICS '2002 Conferernce Proceedings
Download PDF [1.01 MBytes]
Download PPT slides [5.6MBytes]
Bibtex

Abstract: We present Angle-Analyzer, a new single-rate compression algorithm for triangle-quad hybrid meshes. Using a carefully-designed geometry-driven mesh traversal and an efficient encoding of intrinsic mesh properties, Angle-Analyzer produces compression ratios 40\% better in connectivity and 20\% better in geometry than the leading Touma and Gotsman technique for the same level of geometric distortion. The simplicity and performance of this new technique is demonstrated, and we provide extensive comparative tests to contrast our results with the current state-of-the-art techniques.


remeshed meshes

Interactive Geometry Remeshing 
Pierre Alliez, Mark Meyer and Mathieu Desbrun
In SIGGRAPH '2002 Conference Proceedings
Download PDF [14.0 MBytes]
Download PPT slides [14 MBytes]
Bibtex

Abstract: We present a novel technique, both flexible and efficient, for interactive remeshing of irregular geometry. First, the original (arbitrary genus) mesh is substituted by a series of 2D maps in parameter space. Using these maps, our algorithm is then able to take advantage of established signal processing and halftoning tools that offer real-time interaction and intricate control. more...

 

 
Intrinsic Parameterizations of Surface Meshes
Mathieu Desbrun, Mark Meyer and Pierre Alliez
In EUROGRAPHICS '2002 Conference  Proceedings (second best paper award)
Download PDF [6MBytes]
Download PPT slides [39 MBytes]
Bibtex

Abstract: Parameterization of discrete surfaces is a fundamental and widely-used operation in graphics, required, for instance, for texture mapping or remeshing. As 3D data becomes more and more detailed, there is an increased need for fast and robusttechniques to automatically compute least-distorted parameterizations of large meshes. In this paper, we present newtheoretical and practical results on the parameterization of triangulated surface patches more...

 

Efficient View-dependent Refinement of 3D Meshes using Sqrt(3)-Subdivision
Pierre Alliez, Nathalie Laurent, Henri Sanson and Francis Schmitt
the Visual Computer, vol 18(4), 2003
Download PDF [3.65 MBytes]
Bibtex

Abstract: In this paper we introduce an efficient view dependent refinement technique well-suited to adaptive visualization of 3D triangle meshes on a graphic terminal. Our main goal is the design of fast and robust smooth surface reconstruction from coarse meshes more...

 

Valence-Driven Connectivity Encoding for 3D Meshes
Pierre Alliez and Mathieu Desbrun
In EUROGRAPHICS '2001 Conference Proceedings
Download PDF [2.96 MBytes]
Download PPT slides [8.44 MBytes]
Bibtex

Abstract: In this paper, we propose a valence-driven, single-resolution encoding technique for lossless compression of triangle mesh connectivity. Building upon a valence-based approach pioneered by Touma and Gotsman, we design a new valence-driven conquest for arbitrary meshes that always guarantees smaller compression rates than the original method more...

 

Progressive Encoding for Lossless Transmission of 3D Meshes
Pierre Alliez and Mathieu Desbrun
In ACM SIGGRAPH '01 Conference Proceedings
Download PDF - 1200 dpi [10 MBytes]
Download PDF - 300 dpi [2.45 MBytes]
Download PPT slides [9.29 MBytes]
Bibtex

Abstract: Lossless transmission of 3D meshes is a very challenging and timely problem for many applications, ranging from collaborative design to engineering. Additionally, frequent delays in transmissions call for progressive transmission in order for the end user to receive useful successive refinements of the final mesh. In this paper, we present a novel, fully progressive encoding approach for lossless transmission of triangle meshes with a very fine granularity more...

 

Mesh Approximation using a Volume-Based Metric
Pierre Alliez, Nathalie Laurent, Henri Sanson and Francis Schmitt
In PACIFIC GRAPHICS '99 Conference Proceedings
Download PDF [2.7 MBytes]
Bibtex

Abstract: In this paper we introduce a mesh approximation method that uses a volume-based metric. After a geometric simplification, we minimize the volume between the simplified mesh and the original mesh using a gradient-based optimization algorithm and a finite-element interpolation model implicitly defined on meshes more...

 

Removing Degeneracies by Perturbing the Problem or the World
Pierre Alliez, Olivier Devillers and Jack Snoeyink
In CCCG '98 Conference Proceedings 
Bibtex

Abstract: We describe two problem-specific approaches to remove geometric degeneracies that we call perturbing the problem and perturbing the world.  Using as our primary examples 2-d and 3-d Delaunay triangulation with Euclidean and polygonal metrics, we show that these approaches lead to relatively simple and efficient perturbations of the points that do not depend on a fixed ordering or index.  Thus, they produce canonical output, which is important for producing test suites and verifiers for randomized or dynamic geometric algorithms.