Parallel Robots: Open Problems
Jean-Pierre MERLET
INRIA, BP 93,
06902 Sophia-Antipolis, France
E-mail: Jean-Pierre.Merlet@sophia.inria.fr
In the past recent years parallel robots have drawn a lot of interest
in the robotics community and in many applicative domains: medical,
machine-tools, pick-and-place,etc, where the advantages (e.g.
accuracy, rigidity, high velocity) of closed-loop chains may be
useful. The purpose of this paper is to identify
important open theoretical problems in this field.
In the past recent years parallel robots have drawn a lot of interest
in the robotics community. This is exemplified by a large increase in
the number of papers published on this subject together with the
application of parallel robots in very different domains1.
However in many cases unexpected
difficulties in the design and control of such system have led to
performances which, although still
better than conventional mechanical architectures, were not exactly what
was expected. In the following sections we will identify open problems
in this field.
A large number of mechanical designs for parallel robots with 2 to 6
DoF have been proposed.
A survey of 82 mechanical architectures proposed in the
literature shows that
40% have 6 DoF, 3.5% 5 DoF, 6% 4 DoF, 40% 3 DoF, the
remaining having 2 DoF. Some systematic approaches for finding
all the possible layouts
of the joints and actuators that leads to robots with specified
number and type of DoF have been
proposed [5,9,16,23,43,51].
In my opinion these approaches have still to be improved as they are
based on simplifying assumptions that discard potentially interesting
architectures. This is exemplified by the small number of robots with
4 and 5 DoF which have been proposed: here one difficulty is that no
robot with identical chains will have such number of
DoF [36].
Another interesting aspect of parallel robots is that they enable to
use unconventional actuators like, for example, wire with
winches [1] or binary linear actuators (having only
two states, fully extended or retracted) [7]. This
enable to extend the application area of parallel robot but at the
same time induces additional constraints on the theoretical problems
to be solved (e.g. computing the workspace not only taking into
account the limits on the stroke of the actuators but also the
preservation of the tension in the wires). Another promising field is
the study of reconfigurable robots in which the location of the
joints may be changed at will to obtain the best robot for the task at
hand [30,50], a problem that we will address in the synthesis section.
Parallel robots may use complex joints like multiple ball-and-socket and
universal joints, whose restricted motions have a large influence on
the workspace volume. New joint designs have been proposed:
with large motion capabilities [20],
flexible for parallel micro-robot [41]. Still improvements
of these joints have received scant attention.
The problem is to determine the pose of the end-effector being
given the articular coordinates. Two approaches may be distinguished
according to the number of sensors which are used:
minimal, i.e. strictly equal to the number of actuated articular
coordinates, or redundant. i.e. greater than this number.
This is clearly an area where a cooperative work with mathematicians
has produced in the last 10 years the most beautiful results.
If we measure only the articular coordinates the direct kinematics
will have, in general, multiple solutions.
As we are interested mainly in the current pose of the platform we may
rely on an iterative scheme, e.g. Newton-Raphson, to calculate this
pose. These schemes need an initial estimate of the solution (which is
in general available) but may experience convergence problem or,
worse, may lead to a solution which does not correspond to the current
pose. Alternate scheme has been proposed to solve this
problem [4,11,13], but without improvement in
the computation time.
Another approach is to first determine all the possible
solutions of the problem and, then, to sort the solutions in order to
determine the current pose. The complexity of finding all the
solutions increase, in general, with the number of DoF of the
end-effector. Note that we may encounter
numerical problems even for simple robot as shown by
Guglielmetti [19] for the Delta robot.
For complex robots the solutions may be determined
either by using a pure numerical method like the
continuation method [42] or by
elimination [14], i.e. by manipulating the equations
of the inverse kinematics
in order to reduce the problem to the solution of an univariate polynomial,
which
real roots enable to determine all
the possibles poses of the end-effector.
Although the former method was able to solve the problem in some cases,
its efficiency seems to be lower than the latter method, on which we
will focus.
A drawback of the elimination method is that it can be performed in
many different ways, not all of them leading to the same degree for
the resulting polynomial.
Therefore to determine the best univariate polynomial, i.e. the one
having the
lowest possible degree, it is necessary to determine a bound on the
number of real solutions of the direct kinematics. Such bounds have been
obtained using either classical, but often forgotten, geometrical
theorems or the most recent results in algebraic geometry. Basically
these bounds are obtained by using analysis theorems, like
Bezout's theorem, which enable to determine
the maximum number of roots of a given system just by inspection
and subtracting from this number all the roots that are at
infinity. This number gives an upper bound of the number of real and
complex roots of the system. Strangely, in many cases it has
always been possible to find a configuration of the robot such that
the number of real solutions of the direct kinematics is exactly the
bound. This is exemplified by the case of the general Gough platform
for which a bound of 40 has been found in 1992 [45]
while an example with
40 real solutions has been found in 1998 [12].
In the elimination method, finding the univariate polynomial
is either tedious and/or mathematically complex. Fortunately
the calculation done for a particular mechanical architecture may
sometime be used for another architecture (e.g. the direct kinematics
of the Hexa robot may be solved by using the algorithm for the
Gough platform).
Still there is some work to be done in this area as the theoretical
algorithms are difficult to use in practice: for example in the case
of the Gough
platform finding the 40th order polynomial for any geometry and
any leg lengths is still a difficult job [25].
Furthermore the manipulation leading to this polynomial are so complex
that they prevent any symbolic factorization, which will lead to a
simplified, faster solution. But this simplification may be possible as shown
for the Stewart platform: the elimination method leads to a 12th order
polynomial but
this polynomial is (at least) the product of two 6th order
polynomials [32].
Clearly this area has not been sufficiently
investigated.
Up to now we have considered only the first step of the solution of
the direct kinematics. Indeed as
we are interested mainly in the current pose of the end-effector, we have to sort the set of
solutions. Possible sorting criterion are that the solution should be
reached from the initial assembly mode, i.e. the pose of the
end-effector when it was first assembled, without crossing a
singularity and without links interference.
At one time it was thought that the former criteria was sufficient to
determine an unique solution. It is now known that this is false
as shown by Innocenti for planar robot [28] and by
Wenger for spatial robot [49]: there exist singularity-free
trajectories joining different solutions of the direct
kinematics. Still singularity analysis
may help to eliminate solutions, but showing that the singularity and
interference criterion will lead to an unique solution is an open
problem, together with an algorithm implementing these criterion.
Another approach to solve the direct kinematics is to add extra sensors to the
robot. Indeed the n articular sensors provide a system of equations
in the n pose parameters: hence each extra sensor will provide an
additional equation, leading to an over-constrained system which,
hopefully will have an unique solution.
The problem is here to determine the
minimal number of sensors and their location in order to have an
unique solution with the simplest analytic form and quite robust with
respect to the sensor errors. Some of these problems have been
addressed in [2,6,21,36,46], but
this issue is far from being solved. Note that adding sensors may play
also an important role in the robot calibration (see the next
section).
Practical use of the inverse and direct kinematics
requires a perfect knowledge of certain geometric elements of
the robot, particularly for accurate robots.
Thus, position control of a
Gough platform needs the locations
of the passive joints (a full model requires 132 parameters [35]).
Even if a quite accurate estimates of these parameters
are available, a calibration may be necessary.
Although
this problem has been solved for serial robots, this is not the case
for parallel robot. Indeed, for a serial robot, small errors in the geometric
parameters of the robot lead, in general, to a large difference between the
real pose of the end-effector and the expected one. This difference
may be evaluated by measuring the pose of the end-effector and
then be used in an optimization procedure which will determine
values of the parameters decreasing the positioning errors.
Applied to parallel robot this method leads to calibration result
that are in general disastrous.
We pay here for one of the advantages of parallel
robot: a large error in a parameter may lead to a
quite small error in the pose of the end-effector. Furthermore the
measurement noise has a large influence on the result of the
calibration process: a rule of thumb for the accuracy of
the poses measurement system is given by
Vischer [47]: this accuracy should be at least
ten times lower that the expected gain in the location of the joints.
This type of calibration method may be called external
calibration as it relies on an external measurement system.
Specific methods of
external calibration have been
proposed [15,38,40,47,53], and in
some cases
theoretical difficulties have been identified. For example Innocenti
has shown that, even in absence of noise in the measurements, the
method proposed by Zhuang may lead to up to 20 different values for the
geometric parameters [27]. Another problem is to
determine the best measurement poses for the calibration: this problem
has been addressed by Nahvi [38] but has led to
impractical result as the poses should be near-singular.
Another approach is the auto-calibration
methods [10]. In that case
either extra sensors are used or mechanical constraints are imposed on
the legs of the robot (e.g. by clamping a leg so that its direction
remains fixed during the calibration). These methods seem to have a
large potential but have received little attention.
The main difficulty of workspace analysis for parallel robot is that,
as the reachable locations of the end-effector are dependent on its
orientation, a
complete representation of the workspace should be
embedded
in a 6-dimensional workspace
for which there is no possible graphical illustration. Only
subsets of the workspace may therefore be represented.
The most investigated workspace is the 3D constant orientation
workspace, which describe the possible location of the origin of the
end-effector for a constant orientation:
geometric or algebraic approaches may be
used [22,17,31], the former being faster and the
latter more general. But many other types of workspace are of
interest, for example the reachable workspace (all the locations
that can be
reached by the origin of the end-effector), the orientation
workspace (all the orientations of the end-effector for a given
location of the origin of the end-effector) or the inclusive orientation
workspace (all the locations
that can be
reached by the origin of the end-effector with every orientation in a
given set). Although the determination of these types of workspace has been
addressed for planar robot [36], they remain largely
ignored for spatial robots. Furthermore they can be complexified at
will by adding constraints (e.g. singularity-free workspace or
workspace with a lower bound on the transmission factor). A related
problem is to find the volume swept by an object lying on the
end-effector [22,34].
A companion problem to workspace analysis is the trajectory planning
problem. This may be understood as to determine first if a given
trajectory between two poses fully lie in the workspace of the robot and is
singularity-free, and, if the answer is negative, find an alternate
trajectory that join the two poses. An interesting variant of this
problem for robots having more DoF than necessary
(e.g. for a 6 DoF milling machine where the rotation around the normal
of the end-effector is not used) is to determine the possible ranges
of the extra DoF which ensure that a given trajectory lie in the
workspace of the robot, with the further problem of determining the
value in these ranges which optimize another criteria (e.g. for which
the maximal value of the articular forces over the trajectory is minimal).
This remains an important topic of study although many progress have
been made in this field e.g. the geometrical classification of the
singularities or algorithms for detecting singularities in a given
workspace [36]. Still a global analysis of singularity in
relation with the workspace and trajectory planning is needed, for
example, to determine if
singularity surfaces split the workspace of a robot into connected
components, a problem which has been addressed only for planar
robot [49] or for special cases of spatial
robots [24]. Another interesting field of study is
parallel robots which are always in a singular configuration. This
type of robot may be of practical interest, but have been studied only
at a theoretical level [26].
Parallel robots may be used with their main axis not directed
along the vertical. Hence for equilibrating the gravity force the
actuators will have to provide forces which may be quite large. Using
counterweights or springs for statically balancing the robot may be of
interest to decrease the size of the actuator. Here the problem is to
determine the location and mass or stiffness of the balancing
elements. This problem has been solved for planar robots [29]
but remains largely open for spatial robots although it has be proven
that it was impossible to balance a Gough platform with
counterweights [33].
Another advantage of the parallel structure is that it enable to
design very fast robot by combining the action of the actuators, while
the low mass of the moving elements induces small inertia forces. This
is exemplified by the performance of the Delta robot which may
reach a peak acceleration of 500
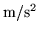 [37].
A first problem here is to determine a tractable dynamic model of the
robot: various formulations may be
used [3,39,44,48,52]
although simplifying assumption have to be made. A second problem is
to implement the algorithm so that the use of the dynamic model will
really improve the motion control of the robot, compared to more
classical control laws. Specific hardware may have to be
used [3,8,18].
A drawback of parallel manipulator is that their performances are
heavily dependent upon the dimensions of the robot and the current pose of the
platform. For example the maximal stiffness over a
given workspace may increase by a factor 7 by only doubling the size
of the mobile platform and similar or larger ratio may be observed
between two different poses. Two problems may be distinguished in this
field: performance evaluation and synthesis.
[37].
A first problem here is to determine a tractable dynamic model of the
robot: various formulations may be
used [3,39,44,48,52]
although simplifying assumption have to be made. A second problem is
to implement the algorithm so that the use of the dynamic model will
really improve the motion control of the robot, compared to more
classical control laws. Specific hardware may have to be
used [3,8,18].
A drawback of parallel manipulator is that their performances are
heavily dependent upon the dimensions of the robot and the current pose of the
platform. For example the maximal stiffness over a
given workspace may increase by a factor 7 by only doubling the size
of the mobile platform and similar or larger ratio may be observed
between two different poses. Two problems may be distinguished in this
field: performance evaluation and synthesis.
Having designed a robot, it is necessary to evaluate its main characteristics:
for example it may be of interest to determine
what will be the extremal values of the articular forces, for a given load
on the end-effector, for any pose within the reachable workspace.
This
is clearly a difficult optimization problem: the analytical expressions of
the articular forces as a function of the pose parameters are complex
expressions involving thousands of terms. We may rely on
a discretisation
method, as we
are usually able to compute numerically the articular forces for a given
pose. But this method is computer intensive and
does not provide an error bound on the result. Alternate methods are
based on the principle that, in general, it is not necessary to
compute exactly the extremal values of the characteristic. Indeed, in
our example, we need to determine the extreme articular forces to choose
the most appropriate actuators among a discrete
set of possible choices. Therefore a method which is able to
provide these values with a guaranteed error will be in
general sufficient, as soon as the error bound may be fixed before
running the algorithm. Although
this type of methods are now becoming available (
for example it is possible to verify efficiently the absence of
singularity within a given workspace
of a given robot [36]) this subject is worthy of study.
Thus, being given a robot and its workspace, finding the extremum of
the articular forces, the passive joint
motions, the generalized velocities of the end-effector for bounded
articular velocities, the stiffness and the forces/torques that can be
applied on the
end-effector for
bounded articular forces are very important practical problems.
Some of these problems are equivalent to the
determination of
the maximal value of the sum of the absolute value of the
pose-dependent elements of
a row of the jacobian matrix of the robot over a given workspace.
A second problem is to determine the geometry of the robot which is
the most suitable for the task at hand. The classical methods of
optimal design, like the cost-function
approach, have difficulties to deal with this problem.
The first difficulty is due to the
large number of parameters that is involved.
But more importantly, the main difficulty come
from the criterion to consider: they are difficult to evaluate (see
previous section), some of them
are antagonistic, or not continuous (for example no
singularity within the workspace). This is clearly a very open
problem.
- 1
-
Albus J., Bostelman R., and Dagalakis N.
The NIST ROBOCRANE.
J. of Robotic Systems, 10(5):709-724,
Juillet 1993
- 2
-
Baron L. and Angeles J.
The on-line direct kinematics of parallel manipulators using
joint-sensor redundancy.
In ARK, pages 127-136, Strobl,
29 Juin-4 Juillet, 1998
- 3
-
Bégon P.
Commande des robots parallèles rapides. Application au robot
HEXA.
Ph.D. Thesis, Université Montpellier II, Montpellier,
23 Juin 1995
- 4
-
Boudreau R. and Turkkan N.
Solving the forward kinematics of parallel manipulators with a
genetic algorithm.
J. of Robotic Systems, 13(2):111-125,
Février 1996
- 5
-
Chakarov D. and Parushev P.
Synthesis of parallel manipulator with linear drive modules.
Mechanism and Machine Theory, 29(7):917-932,
Octobre 1994
- 6
-
Cheok Ka.C., Overholt J.L., and Beck R.R.
Exact methods for determining the kinematics of a Stewart platform
using additional displacement sensors.
J. of Robotic Systems, 10(5):689-707,
Juillet 1993
- 7
-
Chirikjian G.S.
A binary paradigm for robotic manipulators.
In IEEE Int. Conf. on Robotics and Automation, pages
3063-3070, San Diego, 8-13 Mai 1994
- 8
-
Codourey A.
Contribution à la commande des robots rapides et précis.
Application au robot Delta à entrainement direct.
Ph.D. Thesis, EPFL, Lausanne, 1991.
 922.
922.
- 9
-
Danescu G., Jacquet P., and Dahan M.
A solution for the spatial mechanism design.
In IASTED Int. Conf., Applied Modeling and Simulation, Lugano,
20-22 Juin 1994
- 10
-
Daney D.
Self calibration of Gough platform using leg mobility constraints.
In 10th World Congress on the Theory of Machines and
Mechanisms, pages 104-109, Oulu, 20-24 Juin 1999
- 11
-
Didrit O., Petitot M., and Walter E.
Guaranteed solution of direct kinematic problems for general
configurations of parallel manipulator.
IEEE Trans. on Robotics and Automation, 14(2):259-266,
Avril 1998
- 12
-
Dietmaier P.
The Stewart-Gough platform of general geometry can have 40 real
postures.
In ARK, pages 7-16, Strobl,
29 Juin-4 Juillet, 1998
- 13
-
Egner S.
Semi-numerical solution to 6/6-Stewart-platform kinematics based on
symmetry.
Applicable Algebra in Engineering, Communication and Computing,
7(6):449-468, 1996.
- 14
-
Faugère J.C. and Lazard D.
The combinatorial classes of parallel manipulators.
Mechanism and Machine Theory, 30(6):765-776,
Août 1995
- 15
-
Geng Z. and Haynes L.S.
An effective kinematics calibration method for Stewart platform.
In ISRAM, pages 87-92, Hawaï,
15-17 Août 1994
- 16
-
Glazunov V.A. and others .
Classification principles and analysis methods for parallel-structure
spatial mechanisms.
J. of Machinery Manufacture and Reliability, (1):41-49, 1990.
- 17
-
Gosselin C.
Determination of the workspace of 6-dof parallel manipulators.
ASME J. of Mechanical Design, 112(3):331-336,
Septembre 1990
- 18
-
Gosselin C.
Parallel computational algorithms for the kinematics and dynamics of
planar and spatial parallel manipulators.
ASME J. of Dynamic Systems, Measurement and Control,
118(1):22-28, Mars 1996
- 19
-
Guglielmetti P.
Model-Based control of fast parallel robots: a global approach
in operational space.
Ph.D. Thesis, EPFL, Lausanne, 24 Mars 1994
- 20
-
Hamlin G.J. and Sanderson A.C.
A novel concentric multilink spherical joint with parallel robotics
applications.
In IEEE Int. Conf. on Robotics and Automation, pages
1267-1272, San Diego, 8-13 Mai 1994
- 21
-
Han K., W. Chung, and Youm Y.
New resolution scheme of the forward kinematics of parallel
manipulators using extra sensor data.
J. of Mechanical Design, 118(2):214-219,
Juin 1996
- 22
-
Haugh E.J., Adkins F.A., and Luh C.M.
Operational envelopes for working bodies of mechanisms and
manipulators.
ASME J. of Mechanical Design, 120(1):84-91,
Mars 1998
- 23
-
Hervé J.M.
Group mathematics and parallel link mechanisms.
In 9th World Congress on the Theory of Machines and Mechanisms,
pages 2079-2082, Milan, 30 Août-2 Septembre, 1995
- 24
-
Hunt K.H. and McAree P.R.
The octahedral manipulator: geometry and mobility.
Int. J. of Robotics Research, 17(8):868-885, 1998.
- 25
-
Husty M.L.
An algorithm for solving the direct kinematic of
Stewart-Gough-type platforms.
Research Report TR-CIM-94-7, Université McGill, Montréal,
30 Juin 1994
- 26
-
Husty M.L. and Zsombor-Murray P.
A special type of singular Stewart-Gough platform.
In ARK, pages 449-458, Ljubljana,
4-6 Juillet 1994
- 27
-
Innocenti C.
Algorithms for kinematic calibration of fully-parallel manipulators.
In J-P. Merlet B. Ravani, editor, Computational Kinematics,
pages 241-250. Kluwer, 1995.
- 28
-
Innocenti C. and Parenti-Castelli V.
Singularity-free evolution from one configuration to another in
serial and fully-parallel manipulators.
In 22nd Biennial Mechanisms Conf., pages 553-560, Scottsdale,
13-16 Septembre 1992
- 29
-
Jean M. and Gosselin C.
Static balancing of planar parallel manipulators.
In IEEE Int. Conf. on Robotics and Automation, pages
3732-3737, Minneapolis, 24-26 Avril 1996
- 30
-
Ji Z. and Song P.
Design of a reconfigurable platform manipulator.
J. of Robotic Systems, 15(6):341-346, 1998.
- 31
-
Kumar V.
Characterization of workspaces of parallel manipulators.
In ASME Proc. of the 21th Biennial Mechanisms Conf., pages
321-329, Chicago, 16-19 Septembre 1990
- 32
-
Lazard D. and Merlet J-P.
The (true) Stewart platform has 12 configurations.
In IEEE Int. Conf. on Robotics and Automation, pages
2160-2165, San Diego, 8-13 Mai 1994
- 33
-
Leblond M. and Gosselin C.M.
Static balancing of spatial and planar parallel manipulators with
prismatic actuators.
In ASME Design Engineering Technical Conferences, Atlanta,
13-16 Septembre 1998
- 34
-
Masory O. and Wang J.
Workspace evaluation of Stewart platforms.
Advanced robotics, 9(4):443-461, 1995.
- 35
-
Masory O., Wang J., and Zhuang H.
On the accuracy of a Stewart platform-part II: Kinematic
calibration and compensation.
In IEEE Int. Conf. on Robotics and Automation, pages 725-731,
Atlanta, 2-6 Mai 1993
- 36
-
Merlet J-P.
Parallel robots.
Kluwer, Dordrecht, to appear in 1999.
- 37
-
Miller K.
Modeling of dynamics and model-based control of DELTA direct-drive
parallel robot.
J. of Robotics and Mechatronics, 17(4):344-352, 1995.
- 38
-
Nahvi A. and Hollerbach J.M.
The noise amplification index for optimal pose selection in robot
calibration.
In IEEE Int. Conf. on Robotics and Automation, pages 647-654,
Minneapolis, 24-26 Avril 1996
- 39
-
Nguyen C.C. and others .
Trajectory planning and control of a Stewart platform-based
end-effector with passive compliance for part assembly.
J. of Intelligent and Robotics Systems, 6(2-3):263-281,
Décembre 1992
- 40
-
Oliviers M.P. and Mayer J.R.R.
Global kinematic calibration of a Stewart platform.
ASME DSC, 57(1):129-136, 1995.
- 41
-
Pernette E. and others .
Design of parallel robots in microrobotics.
Robotica, 15(4):417-420,
Juillet- Août, 1997
- 42
-
Raghavan M. and Roth B.
Solving polynomial systems for the the kinematic analysis of
mechanisms and robot manipulators.
ASME J. of Mechanical Design, 117(2):71-79,
Juin 1995
- 43
-
Rao A.C.
Topological characteristics of linkage mechanisms with particular
reference to platform type robots.
Mechanism and Machine Theory, 30(1):33-42,
Janvier 1995
- 44
-
Reboulet C. and Berthomieu T.
Dynamic model of a six degree of freedom parallel manipulator.
In ICAR, pages 1153-1157, Pise,
19-22 Juin 1991
- 45
-
Ronga F. and Vust T.
Stewart platforms without computer?, 1992.
Preprint.
- 46
-
Tancredi L. and Teillaud M.
Application de la géométrie synthétique au problème de
modélisation géométrique directe des robots parallèles.
Mechanism and Machine Theory, 34(2):255-269,
Février 1999
- 47
-
Vischer P. and Clavel R.
Kinematic calibration of the parallel Delta robot.
Robotica, 16(2):207-218,
Mars- Avril, 1998
- 48
-
Wang L.C.T. and Chen C.C.
On the dynamic analysis of a general parallel robotic manipulators.
Int. J. of Robotics and Automation, 9(2):81-87, 1994.
- 49
-
Wenger P. and Chablat D.
Workspace and assembly modes in fully parallel manipulators: a
descriptive study.
In ARK, pages 117-126, Strobl,
29 Juin-4 Juillet, 1998
- 50
-
Yang G., Chen I-M., and Yeo S.H.
Design consideration and kinematic modeling for modular
reconfigurable parallel robots.
In 10th World Congress on the Theory of Machines and
Mechanisms, pages 1079-1084, Oulu, 20-24 Juin 1999
- 51
-
Yufeng L. and Tingli Y.
Structure types and characteristics of six degree-of-freedom
closed-chain manipulators with all actuators on base.
In 9th World Congress on the Theory of Machines and Mechanisms,
pages 1795-1799, Milan, 30 Août-2 Septembre, 1995
- 52
-
Zanganeh K.E., Sinatra R., and Angeles J.
Kinematics and dynamics of a six-degree-of-freedom parallel
manipulator with revolute legs.
Robotica, 15(4):385-394,
Juillet- Août, 1997
- 53
-
Zhuang H. and Liu L.
Self calibration of a class of parallel manipulators.
In IEEE Int. Conf. on Robotics and Automation, pages 994-999,
Minneapolis, 24-26 Avril 1996
Footnotes
- ... domains1
-
http://www.inria.fr/coprin/equipe/merlet/merlet_eng.html
J-P. Merlet