COPRIN
(Contraintes, OPtimisation, Résolution
par INtervalles)
Projet commun I3S/INRIA/CERMICS,
Thème 2B1
Mots clés:
Contraintes, optimisation, analyse par intervalles,
consistances, analyse numérique, lien formel-numérique,CAO,
géométrie, génération de jeux de test, théorie des
mécanismes, robotique
Ce document se décompose en une partie synthétique (page 1
à ![[*]](crossref.png) ) suivie d'annexes techniques.
) suivie d'annexes techniques.
Composition de l'équipe
Permanents
COLLAVIZZA Hélène2(Maître de Conférences UNSA)
MERLET
Jean-Pierre3
(Directeur de Recherche INRIA, responsable scientifique)
NEVEU Bertrand
4(Ingénieur en Chef des Ponts et Chaussées, CERMICS)
PAPEGAY Yves5(Chargé de Recherche INRIA)
RUEHER Michel6 (Professeur
UNSA, responsable permanent)
TROMBETTONI Gilles (Maître de Conférences UNSA)
Doctorants
| GOLDSZTEJN Alexandre | Bourse CIFRE (avec Thales) |
| JERMANN Christophe | Allocataire BDI (région, CNRS) |
| MADELINE Blaise | Allocataire MESR & Moniteur |
| ROLLAND Luc | Boursier INRIA (en commun avec le projet SPACES) |
| URSO Pascal | Allocataire MESR & Moniteur |
Ingénieurs
| MICHEL Claude | Ingénieur de recherche (CDD de 18 mois) |
Contacts privilégiés
Nous avons des collaborations étroites avec Y. Lebbah, Maître-assistant à l'Institut d'Informatique, Université d'Oran, F. Rouillier et P. Zimmerman (SPACES).
La thématique de l'actuel projet CONTRAINTES de l'I3S est plus large que celle du projet COPRIN. E. Kounalis (Professeur), J-C. Lafon (Professeur) et J.P. Regourd (Maître de Conférences), membres du projet CONTRAINTES, ne rejoignent pas immédiatement le projet COPRIN, mais nous conservons des contacts privilégiés avec eux.
Introduction
La motivation scientifique à l'origine de cette proposition de
projet est l'intérêt commun pour la résolution de systèmes
de
contraintes. Dans le cadre de ce projet, une contrainte se
définit à partir
d'un ensemble de ![]() relations
relations ![]() dans
dans ![]() impliquant les
impliquant les ![]() inconnues
inconnues
![]() et pouvant utiliser l'ensemble des opérateurs et fonctions
mathématiques usuels (ainsi la fonction
et pouvant utiliser l'ensemble des opérateurs et fonctions
mathématiques usuels (ainsi la fonction
![]() est pour nous admissible).
Les problèmes qui nous intéressent sont d'une part la
satisfaction
de systèmes de contraintes ((
est pour nous admissible).
Les problèmes qui nous intéressent sont d'une part la
satisfaction
de systèmes de contraintes ((![]() ,
, ![]() )), d'autre
part la
recherche d'optimalité ou d'existence de
propriété (il existe une valeur de
)), d'autre
part la
recherche d'optimalité ou d'existence de
propriété (il existe une valeur de ![]() telle que
telle que ![]() , ou
deux
valeurs
, ou
deux
valeurs ![]() ,
, ![]() telles que
telles que ![]() et
et ![]() )
)
Comme on peut le voir, la notion de contraintes est donc très large: de même la notion de solution sera multiforme comme on le verra le long de ce document.
Outre l'intérêt partagé pour ce genre de problèmes, il existe un autre point commun. Chacun des trois partenaires a déjà proposé des méthodes de résolution (approche dite "par contraintes" pour l'I3S/CERMICS et "analyse par intervalles" pour l'INRIA) qui ont en commun d'utiliser l'arithmétique d'intervalles. Partager les mêmes structures de données permet de travailler indifféremment avec des méthodes des deux types et c'est évidemment en jouant sur la complémentarité que nous estimons pouvoir produire une algorithmique efficace (ce travail a d'ailleurs déjà commencé, voir par exemple section 14.4.1).
Programmation par contraintes
La Programmation par Contraintes est un sujet de recherche
qui intègre les travaux de divers
domaines comme les mathématiques discrètes, l'analyse
numérique,
la programmation mathématique ou le calcul formel et qui,
du point de vue académique, est très structurée78.
Cette communauté peut exhiber des
réussites marquantes dans des domaines d'application tels que les
problèmes combinatoires, l'ordonnancement, l'analyse financière,
la simulation et la synthèse de circuits intégrés, le
diagnostic
de pannes, l'aide à la décision, la biologie
moléculaire9,
la résolution de problèmes géométriques10,
etc ![]() . Par exemple, dans les domaines de
l'ordonnancement et de l'allocation de ressources pour le transport
aérien, les sociétés ILOG et CoSYTEC ont développé
des
logiciels d'optimisation pour la gestion du trafic aérien,
utilisés par de nombreux aéroports, ainsi que des
logiciels d'emploi du temps et de rotation de
personnels1112, etc.
Ces résultats positifs ont pu être obtenus pour différentes
raisons:
. Par exemple, dans les domaines de
l'ordonnancement et de l'allocation de ressources pour le transport
aérien, les sociétés ILOG et CoSYTEC ont développé
des
logiciels d'optimisation pour la gestion du trafic aérien,
utilisés par de nombreux aéroports, ainsi que des
logiciels d'emploi du temps et de rotation de
personnels1112, etc.
Ces résultats positifs ont pu être obtenus pour différentes
raisons:
- les outils et méthodes sont d'application très
générale
(par exemple il n'est pas nécessaire de se restreindre à un type
particulier de système), sans évidemment pour autant que
l'obtention d'un résultat soit garantie.
- l'hypothèse de base de la programmation par contraintes
(recherche de solutions dans un domaine borné) est très souvent
naturellement satisfaite dans la pratique où les inconnues
correspondent à des grandeurs physiques,
- par principe même les méthodes sont très appropriées
à une
implantation distribuée qui permet d'en améliorer sensiblement
l'efficacité.
- les méthodes viennent compléter d'autres approches plus sensibles au nombre d'inconnues ou à la structure des équations (par exemple pour les systèmes algébriques).
Nous nous intéressons dans ce projet essentiellement à la résolution et à l'optimisation de systèmes de contraintes non linéaires sur les réels ou de systèmes mixtes (contraintes sur les réels et contraintes sur les entiers ou des ensembles finis de réels). Deux exemples de problème de ce type sont présentés dans l'annexe 6.
Contraintes, Optimisation et Analyse par Intervalles
Le formalisme des contraintes permet de décrire des problèmes d'optimisation et de conception dans des domaines très divers, qui vont du transport à la santé. Nous nous plaçons donc dans un cadre transversal au niveau des applications tout en nous inscrivant dans les axes "Maîtriser l'infrastructure numérique", "Savoir produire des logiciels sûrs" et "Concevoir et maîtriser l'automatique des systèmes complexes" du plan stratégique 1999-2003 de l'INRIA.
Deux concepts sont au
c![]() ur
de notre activité de recherche: l'analyse par intervalles et
la
consistance. Nous allons donner ici quelques
notions
sur ces concepts, illustrés sur des exemples simples mais qui
permettent de comprendre facilement les principes de base. Pour
cela,
il est nécessaire d'introduire l'outil commun à ces deux
approches:
l'arithmétique d'intervalles.
ur
de notre activité de recherche: l'analyse par intervalles et
la
consistance. Nous allons donner ici quelques
notions
sur ces concepts, illustrés sur des exemples simples mais qui
permettent de comprendre facilement les principes de base. Pour
cela,
il est nécessaire d'introduire l'outil commun à ces deux
approches:
l'arithmétique d'intervalles.
Arithmétique par intervalles
L'analyse par intervalles [11] est une technique
relativement ancienne qui consiste à utiliser dans une équation
des intervalles en place des nombres, un intervalle
![]() étant défini comme l'ensemble des
nombres
étant défini comme l'ensemble des
nombres ![]() vérifiant
vérifiant
![]() (pour
des
raisons de simplicité on se contentera ici d'intervalles fermés).
La
différence
(pour
des
raisons de simplicité on se contentera ici d'intervalles fermés).
La
différence
![]() est la largeur de
l'intervalle.
est la largeur de
l'intervalle.
Soit ![]() une fonction de
une fonction de ![]() variables
variables
![]() retournant
un
réel et soit
retournant
un
réel et soit ![]() un ensemble d'intervalles pour chacune des
variables. Considérons une fonction
un ensemble d'intervalles pour chacune des
variables. Considérons une fonction
![]() retournant
un
intervalle
retournant
un
intervalle ![]() :
: ![]() sera appelée une fonction d'évaluation
par intervalle de
sera appelée une fonction d'évaluation
par intervalle de ![]() si
si
![]()
![]() . En d'autres termes
quelles que soient les valeurs prises par les inconnues
dans les intervalles, la valeur de la fonction va être incluse
dans son évaluation par intervalles:
l'évaluation fournit donc des bornes supérieures et
inférieures, souvent
surévaluées, pour la
fonction considérée.
. En d'autres termes
quelles que soient les valeurs prises par les inconnues
dans les intervalles, la valeur de la fonction va être incluse
dans son évaluation par intervalles:
l'évaluation fournit donc des bornes supérieures et
inférieures, souvent
surévaluées, pour la
fonction considérée.
Une manière simple de construire une fonction d'évaluation,
appelée la fonction d'évaluation naturelle, est de
remplacer
chaque inconnue par son intervalle puis de substituer les
opérateurs
mathématiques de la fonction par des équivalents pour
les intervalles (qui retournent des intervalles). Par exemple, on
peut
définir l'opérateur "+" entre 2 intervalles
![]() et
et
![]() par
par
Considérons par exemple la fonction
Cette redéfinition des opérateurs existe pour la plupart des fonctions mathématiques usuelles.
Les fonctions d'évaluation ont de multiples et intéressantes propriétés; nous en mentionnerons simplement deux. La première en est le caractère systématique: la nature mathématique des fonctions à traiter joue un rôle faible puisque l'on peut pratiquement toujours construire une fonction d'évaluation de manière quasiment automatique. Une seconde propriété importante est qu'il est possible de prendre en compte les erreurs numériques de manière à ce que l'évaluation par intervalles contienne de manière certaine le résultat exact de l'opérateur. Par exemple, la valeur 1/3 qui n'a pas de représentation exacte en ordinateur, sera en fait représentée par un intervalle défini par les nombres machine les plus proches de 1/3 et respectivement inférieur et supérieur à cette valeur. En conséquence, la multiplication de la valeur 1/3, représentée par un intervalle, par la valeur 3 donnera un intervalle qui contiendra la valeur 1. Une conséquence directe de cette propriété est que les algorithmes reposant sur l'analyse par intervalles présentent des bonnes caractéristiques de robustesse vis-à-vis des erreurs numériques.
Notons qu'il existe de nombreux logiciels qui implantent de manière efficace les opérations de base de l'arithmétique d'intervalles comme, par exemple, BIAS/Profil13, FORTE C++ Interval arithmetic14, InC++15, INTBLAS16, XSC17. Nous suivons aussi avec beaucoup d'attention les développements fait à l'INRIA de MPFI, une arithmétique d'intervalles reposant sur les structures de données de MPFR.
Notion de consistance
La consistance est une opération qui a pour but de vérifier dans quelle mesure les intervalles actuels pour les inconnues permettent de satisfaire les contraintes et de réduire si possible la largeur de ces intervalles en utilisant les opérations de base de l'analyse par intervalles et des opérations de réécriture des contraintes.
Les consistances utilisées au niveau des problèmes de satisfaction de contraintes (CSP) sur les domaines continus se divisent en deux grandes catégories:
- les consistances strictement locales, c'est-à-dire celles qui ne
travaillent
que sur une seule contrainte,
- les consistances non strictement locales qui vérifient certaines propriétés sur l'ensemble (ou sur un sous-ensemble) du système de contraintes.
Pour illustrer notre propos nous allons donner un
exemple de consistance locale, la 2B-consistance [25], des exemples plus complets se
trouvant en
Annexe 7.
Une contrainte ![]() est
2B-consistante si pour toute variable
est
2B-consistante si pour toute variable ![]() de domaine
de domaine ![]() il
existe des valeurs dans les domaines de toutes les autres variables
qui satisfont
il
existe des valeurs dans les domaines de toutes les autres variables
qui satisfont ![]() lorsque
lorsque ![]() est instanciée avec a et
lorsque
est instanciée avec a et
lorsque
![]() est instanciée avec b. La mise en
est instanciée avec b. La mise en ![]() uvre de la
2B-consistance se fait en utilisant des règles de réécriture
des
contraintes.
uvre de la
2B-consistance se fait en utilisant des règles de réécriture
des
contraintes.
Considérons par exemple l'équation
![]() lorsque
lorsque ![]() est dans l'intervalle [2,4]. Cette équation sera ré-écrite
sous forme de deux relations binaires sans
occurrences multiples de variables :
est dans l'intervalle [2,4]. Cette équation sera ré-écrite
sous forme de deux relations binaires sans
occurrences multiples de variables :
![]() . A
l'aide de ces relations, on génère des fonctions de projection
qui
permettent de calculer les intervalles pour chaque
variable
(valeurs minimales et maximales de chaque variable dans le domaine
délimité par les intervalles initiaux):
. A
l'aide de ces relations, on génère des fonctions de projection
qui
permettent de calculer les intervalles pour chaque
variable
(valeurs minimales et maximales de chaque variable dans le domaine
délimité par les intervalles initiaux):
![]() L'évaluation de ces
fonctions de projection et la propagation des résultats permettent de
réduire
L'évaluation de ces
fonctions de projection et la propagation des résultats permettent de
réduire ![]() à [-16,-4] (fonction (a)) et [-7,-3]
(fonction (c)), donc à [-7,-4]. La fonction (b) permet ensuite de
réduire
à [-16,-4] (fonction (a)) et [-7,-3]
(fonction (c)), donc à [-7,-4]. La fonction (b) permet ensuite de
réduire ![]() à
à
![]() (
(
![]() ). Deux
évaluations supplémentaires des fonctions (b) et (d) suffisent
pour réduire le domaine de
). Deux
évaluations supplémentaires des fonctions (b) et (d) suffisent
pour réduire le domaine de ![]() à l'intervalle vide. Ainsi avec
quelques évaluations de fonctions on a
établi que l'équation n'avait pas de racine dans l'intervalle
considéré.
à l'intervalle vide. Ainsi avec
quelques évaluations de fonctions on a
établi que l'équation n'avait pas de racine dans l'intervalle
considéré.
Méthode d'analyse par intervalles
On voit immédiatement le parti que l'on peut tirer de
l'évaluation
par intervalles pour la résolution de contraintes avec une
stratégie simple de dichotomie. Supposons
que l'on recherche les zéros
de la fonction ![]() pour
pour ![]() dans l'intervalle
[-3,3]. L'évaluation de cette fonction pour l'intervalle initial
conduit à l'intervalle [-0.95,19.08], qui contient 0: il est donc
possible (mais pas certain puisque l'évaluation est surestimée)
qu'il existe un zéro de la fonction dans l'intervalle. On
procède alors à une bissection de l'intervalle initial en
considérant successivement les intervalles [-3,0] et ]0,3]. Pour
l'intervalle ]0,3] l'évaluation par intervalle de la fonction
donne
l'intervalle [0.243,19.08] qui ne contient pas 0: on est donc
assuré
qu'il n'existe pas de zéro de l'équation dans cet intervalle. On
procède de même avec l'intervalle [-3,0]. En continuant ce
processus
de bissection, on parvient à encadrer de manière de plus en plus
précise la racine de l'équation (en l'occurrence -1.2813).
dans l'intervalle
[-3,3]. L'évaluation de cette fonction pour l'intervalle initial
conduit à l'intervalle [-0.95,19.08], qui contient 0: il est donc
possible (mais pas certain puisque l'évaluation est surestimée)
qu'il existe un zéro de la fonction dans l'intervalle. On
procède alors à une bissection de l'intervalle initial en
considérant successivement les intervalles [-3,0] et ]0,3]. Pour
l'intervalle ]0,3] l'évaluation par intervalle de la fonction
donne
l'intervalle [0.243,19.08] qui ne contient pas 0: on est donc
assuré
qu'il n'existe pas de zéro de l'équation dans cet intervalle. On
procède de même avec l'intervalle [-3,0]. En continuant ce
processus
de bissection, on parvient à encadrer de manière de plus en plus
précise la racine de l'équation (en l'occurrence -1.2813).
Cette technique fruste, mais très rapide, permet d'obtenir des intervalles susceptibles de contenir les racines, le processus s'arrêtant lorsque la largeur des intervalles, ou de l'évaluation de la fonction, est inférieure à un seuil donné. On remarquera que cette technique permet de traiter des inégalités et, moyennant une adaptation, de traiter des problèmes d'optimisation. Il faut noter un point important en faveur des méthodes issues de l'analyse par intervalles par rapport à des méthodes alternatives (algébriques, symboliques): comme l'efficacité des méthodes par intervalles est fortement liée aux largeurs des intervalles d'entrée il apparaît clairement qu'en dessous d'un certain seuil sur ces largeurs, ces méthodes ne pourront qu'être plus efficaces. Cependant la technique de base décrite ci-dessus a le défaut majeur de pouvoir conduire à des convergences asymptotiques lentes en raison de problèmes inhérents à l'analyse par intervalles:
- la surestimation des bornes sur
les extréma de la fonction qui est intrinsèque à la méthode
et
dépend malheureusement de l'écriture de la fonction
(l'évaluation de la fonction
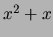 pourra être différente de
celle de
pourra être différente de
celle de 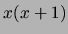 selon l'intervalle sur
selon l'intervalle sur  ),
),
- le caractère indépendant avec lequel sont traitées les équations: on ne prend pas en compte le fait que les équations doivent s'annuler simultanément.
Les consistances partielles (c'est-à-dire non locales) permettent de corriger, dans une certaine mesure, ces deux défauts. Il existe aussi une multitude de techniques qui permettent d'améliorer sensiblement l'efficacité de l'analyse par intervalles (amélioration de l'évaluation, opérateur rétractant ou d'exclusion) qui seront présentées sommairement en section 7.2.
Les limitations de la programmation par contraintes
Dans cette section nous désirons mentionner différents problèmes qui limitent l'efficacité ou l'utilisation des méthodes de programmation par contraintes. Ces problèmes justifieront notre programme de recherche et sont repris plus en détail dans l'Annexe 8.La plupart des classes de problèmes de satisfaction de contraintes sont NP-complètes. Comme pour beaucoup de méthodes s'attaquant à ce type de problème, l'efficacité d'une approche par contraintes est difficilement prédictible: un changement, même modeste, sur une contrainte ou sur les bornes d'une inconnue peut parfois entraîner des modifications importantes sur le temps nécessaire à la résolution d'un problème donné.
Par ailleurs comme il existe une grande diversité de méthodes pour la résolution de problèmes de contraintes, se pose le choix de la (ou des) méthode(s) qui sera la plus appropriée au problème considéré.
L'efficacité des méthodes développées peut aussi dépendre de la précision de l'arithmétique utilisée: sans que cela soit un axe de recherche du projet, nous nous appuierons pour traiter ce problème sur les travaux d'autres équipes, en particulier de l'INRIA (par exemple ARENAIRE ou SPACES).
Il existe aussi un problème d'interface: la plupart des logiciels de satisfaction de contraintes nécessitent de passer par une phase intermédiaire de portage du problème à traiter dans un symbolisme particulier puis de récupération des résultats, ce qui n'est pas satisfaisant pour l'utilisateur pour qui la solution de systèmes de contraintes n'est qu'une étape dans la résolution globale du problème.
Complémentarité et apport des équipes
La partie du projet issue de l'équipe CONTRAINTES de l'I3S et du CERMICS a une compétence reconnue internationalement dans le domaine des solveurs utilisant les techniques de consistance. Elle entretient d'ailleurs des relations suivies avec ILOG, plusieurs des algorithmes étudiés dans CONTRAINTES ayant été intégrés dans les produits commerciaux comme ILOG Solver. Les applications traitées tournent autour du génie logiciel (jeux de tests, vérification de micro-processeurs) et de la CAO.
La partie du projet issue du projet SAGA de l'INRIA a une compétence reconnue dans l'analyse par intervalles et le calcul formel et dans leur utilisation pour le traitement de problèmes issus principalement de la théorie des mécanismes mais qui sont en voie de diversification (illustrée par exemple par la collaboration avec le projet MIAOU pour la résolution de systèmes liés à des calculs de filtre HF). Par ailleurs, elle maintient des contacts étroits avec des industriels comme CMW, Alcatel, Matra et le CEA et des industriels du Génie Biomédical.
Comme nous allons le voir, la complémentarité de ces deux parties est forte et il y a donc une logique scientifique pour la création d'un projet commun:
- Du point de vue des aspects théoriques, les méthodes de
consistance et d'analyse par intervalles ont les mêmes
objectifs:
l'efficacité des algorithmes ne pourrait que gagner à une
approche hybride, ce que nous avons d'ailleurs déjà démontré
(voir section 3.1).
- Du point de vue des applications, le recouvrement est faible
pour le
moment. On peut noter néanmoins que les trois principales
applications
des deux parties du projet, à savoir les tests logiciels, la CAO
et la
théorie des mécanismes, ont une composante continue importante
et
devraient donc profiter des techniques communes qui seront
développées.
Nous résumons ci-après les points de rencontre entre les deux parties du projet, points qui sont détaillés dans le programme de recherche:
- Complémentarité des travaux provenant des deux
communautés,
informatique et mathématique, qui travaillent sur les intervalles.
Des
compétences à la fois en consistance et en analyse numérique
sont présentes dans COPRIN et le développement d'algorithmes
hybrides
y trouve donc un cadre naturel (voir notamment la
section 3.2
sur le filtrage local, les consistances partielles et l'analyse par
intervalles).
- Intérêt partagé pour le problème, important en
général d'un
point de vue académique, et en particulier pour la conception
optimale, de
trouver des intervalles pour lesquels toutes les valeurs sont
solutions (voir section 6.1).
- Intérêt partagé pour la définition de contraintes
``globales''
en
domaine continu dans le but de simplifier des sous-problèmes
spécifiques pour lesquels un algorithme polynomial de filtrage
pourra
être conçu (voir sections 3.3 et 3.1).
- Intérêt des deux parties pour l'utilisation de l'outil
parallélisation (voir
section 3.2).
- Intérêt pour les techniques générales de
décomposition
d'équations qui peuvent
s'appliquer à des problèmes spécifiques (voir
section 3.1) comme les problèmes de recherche de
conformation de molécules, dans des logiciels de CAO mécanique (voir
section 3.2) ou pour étendre les fonctionnalités d'un
logiciel
de dessin comme xjpdraw
(voir section 14.1). Dans nos solveurs,
les décompositions obtenues servent d'heuristique de choix de la
prochaine variable à bissecter pour les problèmes peu couplés
(voir
section 10.2).
- Attachement commun à des travaux sur la collaboration de
solveurs: l'expérience de la
partie I3S (voir section 3.1) sera mise à profit pour le
développement de la plate-forme logicielle générique
de COPRIN (voir
section 5.7).
Le projet COPRIN se distingue d'autres équipes travaillant dans le même domaine par plusieurs aspects:
- les contraintes que nous traiterons pourront inclure des
objets
mathématiques non considérés par les solveurs actuels (par
exemple des déterminants de matrice, sans qu'il soit nécessaire,
ou
possible, de les développer),
- plutôt que de développer un langage pour la programmation
par
contraintes, nous préférons nous appuyer sur des langages de
calcul formel existants qui permettront de
mettre
les contraintes sous une forme appropriée, d'effectuer des
opérations de pré-traitement complexes, de générer
automatiquement du code pour les solveurs voire de compléter les
résultats obtenus (par exemple une méthode numérique rapide
pour
encadrer les racines et un schéma itératif en formel
pour déterminer les racines avec une précision
arbitraire).
- nous développerons des méthodes pour des systèmes
spécifiques, donc plus efficaces que les algorithmes
généralistes, tout en essayant de préserver une certaine
généricité.
- une grande importance sera attachée à la modularité des
méthodes
pour pouvoir traiter des problèmes où les contraintes ne sont
qu'une partie de la problématique,
- il existe dans le projet des compétences dans des domaines
autres que celui de la résolution de systèmes
(comme le génie logiciel ou la théorie des mécanismes):
nous avons donc à notre disposition une collection de problèmes
effectifs et non académiques et dont en plus
on connaît la difficulté.
En résumé le domaine de COPRIN consiste à combiner des travaux en génie logiciel, calcul formel, programmation par contraintes et analyse par intervalles, pour construire des algorithmes de résolution de systèmes contraints (composés par exemple d'équations et d'inégalités), en particulier pour les systèmes issus de domaines où les membres du projet ont une expertise. Il convient aussi de préciser notre position par rapport aux systèmes algébriques:
- les méthodes algébriques, qui ont l'énorme avantage de fournir bien plus d'informations que les solutions, ont aussi l'inconvénient d'avoir des limites en terme de taille ou de complexité des systèmes que l'on peut traiter,
- Les méthodes hybrides que nous proposons peuvent soit venir à bout (parfois) de systèmes dépassant cette limite, soit présenter un temps de calcul intéressant si l'on recherche des solutions dans un domaine borné.
Les éléments de cette introduction vont être détaillés dans le reste de ce document. On trouvera dans la section ``Programme de recherche'' des considérations sur les développements théoriques qui nous paraissent d'ores et déjà prometteurs ainsi que des descriptions de problèmes liés directement aux applications.
Les sections ``Collaborations scientifiques'' et ``Valorisation'' expliciteront les contacts et les contrats que nous avons déjà, les directions dans lesquelles nous souhaitons développer des collaborations et les moyens que nous utiliserons pour diffuser nos résultats.
Programme de recherche
Nous avons structuré le programme de recherche en quatre parties
principales:
- méthodes de résolution
- outils pour ces méthodes
- données, optimisation et type de solutions
- applications
Méthodes de résolution
Même si l'objet en est le même, les techniques utilisant la consistance diffèrent sensiblement des techniques de l'analyse par intervalles, plus proches de l'analyse numérique. Il est clair que l'efficacité des algorithmes de résolution ne pourrait qu'être améliorée en utilisant une algorithmique hybride mêlant les deux approches, profitant ainsi de la complémentarité des partenaires du projet. Il s'agit donc d'un axe prioritaire de nos recherches, impliquant l'ensemble du projet, et dont l'intérêt est détaillé dans la section 9.1.
Un second thème prioritaire est le développement de solveurs spécifiques qui prennent en compte les particularités de la structure des systèmes à résoudre pour développer des algorithmes spécifiques plus efficaces que les algorithmes généraux, ceci en travaillant à deux niveaux: spécialisation des méthodes de consistance et de test d'unicité, implantation spécialisée des fonctions d'évaluation et de calcul des dérivées. Cet axe de recherche implique plus particulièrement J-P. Merlet, Y. Papegay, G. Trombettoni, M. Rueher. Des exemples illustrant ces deux niveaux sont proposés dans la section 9.2.
Les différents types de solveur ont des efficacités qui varient à
la fois en fonction du problème et des entrées.
Dans l'axe de recherche collaboration entre solveurs, impliquant plus
spécialement M. Rueher,
nous investiguerons
les modes de communication et
d'échanges de données qui autorisent une mise en ![]() uvre
efficace de différents algorithmes et techniques pour la
résolution d'un même problème. Des travaux dans ce sens ont
déjà été entrepris et sont détaillés dans la
section 9.3.
uvre
efficace de différents algorithmes et techniques pour la
résolution d'un même problème. Des travaux dans ce sens ont
déjà été entrepris et sont détaillés dans la
section 9.3.
Outils pour les méthodes de résolution
Les méthodes de résolution décrites dans la section
précédente font appel à des outils communs que nous
allons décrire sommairement dans cette section et dont nous
souhaitons améliorer l'efficacité. En préalable il
convient de mentionner l'utilisation de la parallélisation car, par
essence, les
méthodes par contraintes y sont favorables. Même si les techniques de
parallélisation ne constituent pas un axe de recherche du projet, nous
comptons utiliser des
mécanismes bien connus comme pvm
18 ou mpi
19
et prévoir l'implantation de nos algorithmes
de manière à en permettre une parallélisation via ces
mécanismes. Pour la mise en Dans le même registre, il convient de mentionner des travaux en cours sur la représentation de base des intervalles à l'aide de nombres en précision arbitraire, utilisant les structures MPFR développées par le projet SPACES (travail auquel participe un ancien doctorant de SAGA, David Daney, dans le cadre d'un post-doctorat): s'il ne s'agit pas à proprement dit d'un de nos axes de recherche, il est clair que le résultat de ce travail sera utilisé dans nos algorithmes.
L'axe de recherche techniques de filtrage, dans lequel sont impliqués H. Collavizza, B. Neveu, Y. Papegay, M. Rueher, G. Trombettoni, a comme objectif le développement d'algorithmes polynomiaux (comme par exemple les 2B et 3B-consistance) pour la réduction des intervalles dans lesquels on recherche les solutions. La section 10.1 décrit plus précisément les techniques que nous comptons développer.
L'axe de recherche choix des variables de bissection a comme objectif de déterminer quelles sont la ou les variables pour lesquelles la dichotomie permettra d'obtenir le maximum d'informations sur le système (par exemple prouver l'absence de solution par une dichotomie sur une seule variable). La section 10.2 présente un panorama des techniques existantes et les problèmes que nous aborderons. Ce problème sera plus spécifiquement traité par J-P. Merlet, B. Neveu, M. Rueher, G. Trombettoni.
Notre recherche sur le thème décomposition a comme objectif de couper un problème en sous problèmes indépendants ou faiblement corrélés, la réduction de taille permettant une résolution plus rapide et/ou d'aborder des problèmes trop gros pour être traités dans leur globalité (par exemple la conformation de grosses molécules en biologie moléculaire). L'annexe 10.3 fournit des détails techniques sur les méthodes que nous comptons utiliser, qui seront développées par B. Neveu, G. Trombettoni.
L'axe recherche arborescente, impliquant B. Neveu, G. Trombettoni, a comme but de guider le parcours des branches pour atteindre au plus vite l'objectif désiré. La stratégie de parcours des branches joue en effet un rôle crucial sur l'efficacité. La section 10.4 présente en détail la problématique et les techniques qui peuvent être employées.
Données, optimisation et type de solutions
Pour ce qui concerne les données, notre approche permet de
traiter les fonctions s'exprimant à l'aide de la quasi-totalité
des fonctions mathématiques élémentaires mais aussi celles qui
n'ont pas une forme analytique (ou une forme trop complexe) mais qui sont
calculables à partir d'un processus opératoire (comme
par exemple les
déterminants de matrice).
La programmation par contraintes est un outil approprié pour résoudre des problèmes d'optimisation globale lorsque le problème est soumis à des contraintes complexes. De nombreuses équipes travaillent sur ce problème mais dans cet axe, impliquant plus spécifiquement J-P. Merlet, B. Neveu, M. Rueher, nous nous attacherons à la résolution de problèmes particuliers qui sont présentés plus en détail dans la section 11.2.
Deux grands types de solution peuvent être obtenus avec des méthodes d'intervalles: soit des boîtes contenant les solutions (mais aussi des points non solution), soit des boîtes ne contenant que des solutions (mais certaines solutions peuvent ne pas être obtenues). Il existe des cas où les solutions du deuxième type sont effectivement celles recherchées (par exemple en conception optimale, voir section 6.1) et dans l'axe type de solution J-P. Merlet, B. Neveu et M. Rueher s'intéresseront à la spécialisation des algorithmes dans ce but. La section 11.3 présente des exemples de problème de ce type et la méthodologie que nous comptons employer dans ce cas.
Domaines d'application
Comme nous l'avons mentionné, il est difficile de prédire le comportement des algorithmes de contraintes sur un problème donné. Il est donc nécessaire de procéder à de nombreux tests sur des systèmes très divers pour obtenir des informations sur le comportement "moyen" des algorithmes. Dans ce cadre, le traitement d'applications très diverses est un besoin essentiel pour le projet puisqu'il fournit de nombreux exemples non académiques (et, de plus, permet éventuellement de répondre à des problèmes effectifs).
Puisqu'il existe des industriels développant des solveurs, un premier axe évident pour les applications est l'intégration de nos méthodes dans les outils existants (par exemple ILOG Solver, CHIP, ...).
Outre cet axe nos domaines d'application privilégiés sont, par ordre de priorité croissant, la génération automatique de jeux de tests logiciels et la théorie des mécanismes qui inclut un effort en CAO mécanique. Pour ce dernier thème la validation des résultats pourra nous amener à aller au delà de la simple validation logicielle, jusqu'à la réalisation de prototypes. Les axes de recherche sur ces thèmes sont détaillés dans la section 12.
Programme de travail à moyen terme
Sur le moyen terme nous comptons porter nos efforts sur l'implantation d'une plate-forme logicielle générique qui comprendra la quasi-totalité des méthodes de consistance et d'analyse par intervalles pour la résolution de contraintes. Cette plate-forme a comme objectifs:- d'expérimenter ces méthodes sur des problèmes divers afin de construire une connaissance sur leur efficacité en fonction des problèmes traités,
- de permettre l'intégration aisée de nouvelles méthodes.
Cet effort d'implantation s'accompagnera d'une réflexion théorique sur chaque méthode afin d'en déterminer les limitations et de les améliorer. Les problèmes traités seront principalement des problèmes de grande taille ou pour lesquelles il n'existe pas de méthode permettant d'obtenir ne serait ce qu'une solution.
Le second axe de notre effort portera sur le développement de solveurs spécifiques, en particulier pour les équations de distance et les systèmes algébro-trigonométriques, pour lesquelles des opérateurs spécifiques seront développés. la structure spécifique du système sera utilisée pour améliorer l'efficacité des opérateurs "généralistes" et pour développer de nouveaux opérateurs adaptés au problème.
Collaborations scientifiques
État des lieux
La communauté de recherche sur les contraintes est très active mais parfois disparate en raison des problèmes traités ou des approches (langages, IA, numérique). De nombreuses conférences dédiées à ce sujet (par exemple CP, PACT) ou avec des sessions dédiées à ce sujet (AAAI, IJCAI, INFORMS, IMSP) sont régulièrement organisées et des revues sont consacrées à ce domaine (par exemple Constraints) ou acceptent des articles sur ce thème (par exemple Reliable Computing, Journal of Artificial Intelligence). Bien entendu, le caractère transversal de nos applications et notre désir de transfert nous permettra de publier dans des journaux dédiés à d'autres domaines scientifiques.
Les équipes dans le monde
Au niveau international, sans prétendre à l'exhaustivité, on peut mentionner les principales équipes actives dans ce domaine:
- Constraint Computation Center (University of New Hampshire, Eugene C. Freuder) : fondements et applications des contraintes sur les domaines finis.
- Brown University (Pascal Van Hentenryck) : contraintes dans les domaines continus (réalisation de Newton, Numerica, Localizer, OPL)
- Programming Systems Lab /DFKI Universität des Saarlandes (G. Smolka, Peter Van Roy, A. Podelski): langages concurrents et distribués avec contraintes (développement de Mozart et Oz)
- University of Melbourne (P. Stuckey, M. Maher, K. Marriott): programmation logique avec contraintes
- Center for Planning and Ressource Control (Imperial College): laboratoire où a été développé Eclipse
- Constraint programming group (University of Essex)
- Computational Intelligence Research Laboratory (University of Oregon): utilisation des contraintes pour la représentation des connaissance et le raisonnement
Les équipes en France
En France, les principales équipes, hors INRIA, travaillant sur les problèmes de contraintes sont :
- Contraintes sur les domaines finis et optimisation combinatoire: LIRMM Montpellier (Christian Bessière) , INRA et ONERA Toulouse (Thomas Schiex, G. Verfaillie)
- Programmation logique avec contraintes: LIM Marseille (A. Colmerauer), École des Mines et Université de Nantes (P. Boizumault, F. Benhamou) , LIB Besançon (Bellegarde, B. Legeard), LIRSIA, Université de Dijon (J.J. Chabrier).
Les logiciels
Parmi les logiciels disponibles, on peut mentionner au niveau industriel les produits ILOG (Solver, Scheduler , CPLEX,...), Cosytec (CHIP), Bouygues (Claire) et de Prologia (Prolog III, Prolog IV). Au niveau académique on peut citer CLP(FD) (INRIA LOCO), ECLIPSE (Imperial College), Declic (Université de Nantes), QUAD-CLP/RISC-CLP (Risc Linz).
On peut noter que l'ensemble de ces logiciels présentent un caractère spécifique, soit qu'ils s'attaquent à un problème particulier soit par la nature du domaine pour les inconnues.
Positionnement par rapport aux projets INRIA
Nous avons identifié différents projets de l'INRIA dont les axes de recherche peuvent avoir une intersection avec les objectifs de COPRIN. Il s'agit des projets ou actions ARENAIRE, CONTRAINTES, ESTIME, GALAAD, IDOPT, LANDE, NUMOPT, PROTHEO, SPACES. Par ailleurs des collaborations sont déjà existantes avec MIAOU et pourraient l'être avec ORION (pilotage de programmes) et PRISME (calcul robuste de prédicats géométriques). La section 13 décrit plus en détail ces intersections ainsi que les collaborations possibles ou existantes.
Collaborations existantes
Théorie des mécanismes
C'est un domaine d'application de nos méthodes dans lequel
nous
avons, pour des raisons historiques, des contacts établis de
longue
date.
En France nous avons des contacts suivis avec le CERT-DERA de Toulouse, l'YRCCYN de Nantes, le LIRMM de Montpellier, le Laboratoire de Mécanique Appliquée de Besançon et le laboratoire de Robotique de Paris.
Au niveau européen, nous avons des contacts réguliers avec les Universités de Cassino (M. Ceccarelli), Pise (P. Dario), Bologne (C. Innocenti), Lausanne (P. Myszkorowski), Innsbruck (M. Husty), Wroclaw (Pr. Koch).
Pour ce qui concerne les US et le Canada, nous entretenons une collaboration très active avec l'Université McGill de Montréal (Pr. J. Angeles), avec l'Université de Laval (Pr. C. Gosselin) et avec l'Université de Stanford (Pr. B. Roth). Nous maintenons aussi un contact continu avec C. Wampler du centre de recherche de General Motors pour l'application des méthodes d'homotopie en théorie des mécanismes.
En Asie, nous avons une collaboration continue avec le Pr. Arai de l'Université d'Osaka (cette collaboration s'est traduite par de fréquents séjours, l'écriture d'articles en commun et le co-encadrement de post-doctorants) ainsi qu'une collaboration active avec le Pr. Perng de l'Université Tsing Hua de Taiwan. Par ailleurs nous collaborons avec le Pr. M. Shoham du Technion d'Haifa dans le cadre d'un projet commun de micro-robot.
Contraintes
Au niveau international, nous avons une collaboration active avec Pascal Van Hentenryck (Université de Brown) qui doit effectuer un séjour d'un mois dans notre équipe en 2001. Nous avons également une collaboration avec Véronica Dahl et Hassan Ait Kaci (Simon Fraser University, Vancouver) sur les applications des contraintes au niveau linguistique. Andreas Podelski (Universität des Saarlandes) a effectué un séjour dans notre laboratoire et nous avons gardé des contacts réguliers.
Des échanges réguliers ont lieu avec l'équipe de Boi Faltings à l'EPFL en Suisse, suite à des travaux de collaboration concernant les intervalles et la CAO. Des échanges ont eu lieu l'an dernier avec l'Université technique de St Gallen en Suisse (avec visite de Jermann et Trombettoni sur place pendant une semaine et l'invitation de Rainer Weigel pendant 1 mois à l'I3S), en vue de l'intégration d'un solveur de contraintes géométriques dans leur outil commercial de CAO ClassCAD.
Nous venons d'entamer une collaboration avec le Pr. A. Neumaier de l'Université de Vienne qui est resté dans le projet une semaine en Septembre 2001. Cette collaboration s'est avérée très fructueuse et va se poursuivre en 2002 puisque A. Neumaier a obtenu un financement d'un mois de professeur invité à l'Université de Nice.
Au niveau français, nous avons depuis plusieurs années des contacts étroits avec l'équipe de l'école des Mines de Nantes (séminaires, échanges d'étudiants et Post Docs) ainsi qu'avec l'équipe du LIB (Besançon). Nous entretenons aussi des contacts réguliers avec plusieurs membres du LIM. Une collaboration plus étroite s'est récemment mise en place avec Nicolas Prcovic (LIM, Marseille) sur les algorithmes de recherche arborescente.
Nous entretenons aussi une collaboration de longue date avec J-P. Dedieu et J-C. Yakoubsohn (Laboratoire de Mathématique pour l'Industrie et la Physique, Toulouse ) qui s'est concrétisée par des échanges de logiciel et l'organisation commune de la manifestation SEA. Nous comptons maintenir nos liens avec cette équipe, en particulier pour examiner l'intérêt des méthodes d'exclusion dans les systèmes de contraintes.
Activités nationales
Nous avons depuis 1992 participé aux différents groupes de travail nationaux (Contraintes Flexibles, RESSAC) qui ont rassemblé la communauté de recherche sur les contraintes en domaines finis et ont créé les journées nationales annuelles sur la résolution pratique des problèmes NP-complets (JNPC). Bertrand Neveu et Gilles Trombettoni sont membres du comité de programme de JNPC. Bertrand Neveu préside ce comité de programme pour 2001.
Nous participons aussi au GDR Alp ainsi qu'aux JFPLC (Michel Rueher a été plusieurs fois membre du comité de programme). Nous sommes aussi impliqués dans le groupe Ensemble qui vient de se créer sur l'application de l'analyse par intervalles en commande. Par ailleurs nous collaborons avec des équipes du CNRS dans le cadre d'une Action Spécifique du département STIC et d'un projet ROBEA (Robotique et Entité Artificielle).
J-P. Merlet est membre suppléant de la Commission de Spécialistes, section 61, de l'UNSA. Michel Rueher est Président du comité des Projets de l'I3S et Vice-Président de la Commission de Spécialistes, section 27, de l'UNSA.
Activités internationales
J-P. Merlet est président depuis le 1/1/1998 du Comité Technique "Computational kinematics" de la Fédération Internationale sur la des Machines et des Mécanismes (IFToMM). A ce titre, il est à l'origine de la création du journal électronique (EJCK) sur le thème "Computational Kinematics" qui a vu le jour en 2000. Il est par ailleurs membre de plusieurs comités de programme de conférences et a été le "General Chairman" de la conférence CK qui s'est tenu en 2001 à Séoul. Il est par ailleurs régulièrement consulté comme expert par l'ANVAR, l'INSERM, la Communauté Européenne, la NSF, le FCAR (Canada) et le Ministère de la Recherche Italien.
Au niveau européen, nous comptons participer au groupe de travail sur les contraintes de l'ERCIM. Nous sommes aussi impliqués dans la proposition RTN ``Constraint Solving and Constraint Programming'' coordonnée par F. Fages et qui a été présentée en mai 2001.
Valorisation
Comme nous l'avons mentionné, le projet COPRIN est de nature transversale au niveau des applications même si au démarrage du projet des domaines particulièrement prometteurs ont été identifiés: jeux de tests logiciels, CAO mécanique, théorie des mécanismes.
Nous allons évoquer ici les interlocuteurs avec lesquels nous avons déjà travaillé, les travaux impliqués et nous conclurons par une partie prospective.
Contrats industriels actuels
Nos principaux contrats portent actuellement sur le développement
et
l'intégration d'algorithmes dans des solveurs de contraintes
généralistes, la mise en ![]() uvre des contraintes sur des
nouveaux
domaines d'application
et la conception optimale de mécanismes.
uvre des contraintes sur des
nouveaux
domaines d'application
et la conception optimale de mécanismes.
- Contrat avec Thales ``Systèmes Aéroportés'' (ex Thomson Detexis, anciennement ``Dassault Electronique'') depuis 1991: 2 allocations CIFRE, plusieurs études, un contrat RNTL en cours sur la génération automatique de jeux de test; cette collaboration sera bien entendu poursuivie dans le cadre du projet COPRIN.
- Contrat avec Amadeus sur la mise en
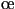 uvre des contraintes
dans
des applications
de tarification aérienne;
uvre des contraintes
dans
des applications
de tarification aérienne;
- nous avons travaillé depuis de nombreuses années sur la conception optimale de robot parallèle avec des partenaires qui sont principalement des PME travaillant dans les technologies de pointe. Mentionnons les contrats avec l'ESRF, Synchrotron de Grenoble, 1992-1998 (développement de positionneurs ultra-précis pour des charges lourdes dont une soixantaine sont en cours d'utilisation actuellement), Constructions mécaniques des Vosges, CMW, (1996-) avec qui nous maintenons un partenariat conjoint avec le projet SPACES pour le développement d'une machine-outil à structure parallèle, ALM, filiale d'Air Liquide, 1997 (développement de table chirurgicale), Alcatel-Deltalab 2000-2001 (positionneurs fins pour le test d'antennes satellite)
D'un point de vue théorique, ces contrats tournent tous autour d'axes de recherche présentés dans les objectifs du projet : satisfaction de contraintes et recherche d'optimum. Il conviendra cependant d'inclure de manière encore plus importante des méthodes de satisfaction de contraintes dans nos travaux sur la conception de systèmes.
Autres contacts
Dans une période récente, nous avons eu des contacts avec Simulog (C. Garnier) pour la simulation de suspensions automobiles et de mécanismes de direction, avec Dassault (A. Leutier) et Top Solid pour des applications de la satisfaction de contraintes dans des systèmes de CAO, avec le CEA-CESTA pour la conception de système dans le cadre du projet MégaJoule, avec Micro Contrôle pour le développement de positionneurs parallèles et avec l'Institut Laue Langevin de Grenoble (collaboration qui devrait très rapidement conduire à un contrat d'étude).
Nous avons de fréquents contacts avec l'équipe de développement ILOG à Sophia Antipolis (publications communes, ILOG intervient comme partenaire industriel dans la BDI de C. Jermann) et nous avons aussi des contacts avec Y. Caseau (Bouygues).
Prospective
Dans un premier temps, nous ne désirons pas établir des contacts dans des domaines autres que ceux précédemment mentionnés: il nous paraît en effet préférable de nous concentrer vers l'établissement d'une panoplie d'outils de base (en particulier des algorithmes hybrides consistance-analyse par intervalles) spécialisés avant de rechercher de nouvelles applications. Il est en effet évident que d'une part cette algorithmique va nécessiter des efforts importants tant du point de vue théorique que de l'implantation et que d'autre part les domaines qui font l'objet de nos recherches actuelles nous fournissent déjà une grande diversité de problèmes.
Mais, bien entendu, nous ferons preuve d'un grand pragmatisme dans l'implantation de cette politique en particulier s'il s'avère que des problèmes dans d'autres domaines industriels peuvent être résolus par des adaptations simples des algorithmes existants.
Les membres du projet portent une attention particulière à la diffusion des résultats obtenus dans le cadre de leur recherche. En plus des publications d'articles (consultables via le WEB), nous avons des activités fortes en enseignement, en organisation de colloques et dans la diffusion de logiciels.
Enseignement
- Jean-Pierre Merlet assure des cours de robotique et de
conception de mécanismes à l'ISIA, à l'Ecole des Mines de Paris,
à l'ESSI et à l'ENSTA. Il intervient aussi ponctuellement dans des
DESS de Génie Biomécanique.
- Michel Rueher, Bertrand Neveu et Gilles Trombettoni
assurent des cours de programmation
par contraintes à l'ESSI, au DEA et en maîtrise d'informatique
de l'Université de Nice.
- Hélène Collavizza est responsable de la première
année de l'ESSI et Michel Rueher est responsable de la filière LOG
de l'ESSI.
- Hélène Collavizza, Bertrand Neveu, Michel Rueher et Gilles
Trombettoni assurent des cours en algorithmique, logique,
programmation en logique, intelligence artificielle, bases de données,
architecture des ordinateurs, assembleur, systèmes d'exploitation, C,
Java à l'Ecole des TPE à Lyon, à l'ESSI et en IUT GTR.
Séminaires et Colloques
Notre expérience indique que les méthodes de satisfaction de contraintes restent encore peu connues des chercheurs d'autres disciplines et des industriels, d'où un besoin clair de diffusion des méthodes.
Pour favoriser une certaine dissémination, outre la participation à des congrès spécialisés, il paraît nécessaire de présenter des travaux montrant comment les méthodes de contraintes permettent de résoudre des problèmes effectifs, en particulier dans des congrès de robotique et de théorie des mécanismes où nos méthodes ont déjà fait leurs preuves.
Du point de vue industriel, la résolution de problèmes issus des domaines d'application déjà mentionnés sera un élément majeur de dissémination. Dans ce cadre, un séminaire réunit déjà régulièrement depuis 1998 les membres de l'équipe avec des membres de la société ILOG et nous comptons intensifier cette activité.
Web
La communauté de recherche sur les contraintes est très structurée et dispose déjà d'une page web où sont centralisées des indications sur les méthodes, personnes, logiciels et benchmarks20. Cependant, pour des raisons historiques, elle est relativement faible sur les méthodes issues de l'analyse numérique et sur les méthodes hybrides. Il paraît donc nécessaire de mettre en avant, au sein de ces archives, l'intérêt des méthodes hybrides. Le serveur Web du projet, outre ses rubriques habituelles, pourra comporter une zone où il sera possible de soumettre des problèmes dans un cadre de conseil.
Logiciels
Le développement d'une plate-forme logicielle constituera une des
activités majeures du projet dès son démarrage. Il s'agira d'un
logiciel générique permettant à la fois le test
des outils existants sur un problème donné ainsi que le
développement de nouvelles méthodes dans le cadre d'un formalisme
commun. Il s'agira d'un prototype que nous comptons mettre à
disposition librement, dans un cadre juridique à déterminer.
Cette plate-forme sera développée en langage C/C++ et s'appuiera sur des structures de données et certaines méthodes déjà existantes. Un état des lieux de l'existant se trouve à l'annexe 14.
Ce projet logiciel est motivé par un manque de logiciels libres comparables qui auraient pu en constituer la base et par la nécessité de validation expérimentale des techniques21.
Nous porterons un soin particulier à la possibilité d'interfacer cette plate-forme générique avec des logiciels de calcul généraliste, en particulier de calcul formel, éventuellement en s'appuyant sur leurs capacités de traitement pour améliorer l'efficacité de la résolution.
Cette plate-forme générique pourra servir de base au développement de logiciels spécifiques, en collaboration éventuelle avec des industriels.
Annexe: Exemples de problèmes
Les problèmes de satisfaction de contraintes (CSP) jouent un rôle essentiel dans de nombreuses applications. Donnons en deux exemples dans le domaine de la conception optimale de systèmes paramétrés et la génération automatique de jeux de tests logiciels.
Un premier exemple: conception optimale de
systèmes
Un système, qu'il soit mécanique, électrique ou autre, peut
être
décrit par des relations explicites ou implicites entre les
entrées
![]() et les sorties
et les sorties ![]() , relations qui dépendent
des paramètres
, relations qui dépendent
des paramètres ![]() définissant la
"géométrie" du système (par exemple
la valeur d'une résistance dans un circuit électrique). On aura
donc en général à disposition des relations du type:
définissant la
"géométrie" du système (par exemple
la valeur d'une résistance dans un circuit électrique). On aura
donc en général à disposition des relations du type:
- les entrées
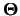 seront dans un domaine borné
seront dans un domaine borné
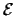 (par exemple la tension d'entrée d'un circuit
électrique doit être dans un intervalle donné),
(par exemple la tension d'entrée d'un circuit
électrique doit être dans un intervalle donné),
- les paramètres
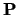 peuvent correspondre à des grandeurs
physiques
qui conduisent à les borner naturellement.
Notons que ces bornes peuvent
être un intervalle ou être décrite par un
ensemble de valeurs discrètes,
peuvent correspondre à des grandeurs
physiques
qui conduisent à les borner naturellement.
Notons que ces bornes peuvent
être un intervalle ou être décrite par un
ensemble de valeurs discrètes,
- la réalisation physique des paramètres
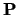 peut être
imparfaite
(sa valeur réelle est dans un intervalle),
peut être
imparfaite
(sa valeur réelle est dans un intervalle),
- le système n'est à étudier que pour des sorties
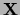 dans un domaine borné
dans un domaine borné 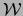 .
.
Ces propriétés peuvent être illustrées sur l'exemple de la conception d'un robot: dans ce cas, les entrées
Comme exemple de contraintes du type (2) considérons
l'imprécision
![]() sur la position de la main
sur la position de la main ![]() due
à l'imprécision des capteurs qui mesurent les
due
à l'imprécision des capteurs qui mesurent les ![]() . L'imprécision
. L'imprécision
![]() dépend à la fois
de la position de la main et des paramètres
dépend à la fois
de la position de la main et des paramètres ![]() :
:
Il s'agira alors de s'assurer que pour toutes les valeurs possibles de
Pour ce qui concerne les contraintes du type (3) on peut avoir à s'assurer, par exemple, que pour toutes les valeurs possibles de
sous les contraintes:
Le problème de la conception optimale se décline en deux volets:
- être capable de déterminer si un système défini par des
valeurs particulières pour les paramètres
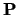 satisfait les contraintes. C'est le plus souvent
un difficile problème d'optimisation sous contraintes
pour lesquelles il faudra garantir l'obtention de l'extremum global ou d'un encadrement de cet extremum.
satisfait les contraintes. C'est le plus souvent
un difficile problème d'optimisation sous contraintes
pour lesquelles il faudra garantir l'obtention de l'extremum global ou d'un encadrement de cet extremum.
- être capable de déterminer soit l'ensemble des valeurs
possibles des paramètres
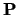 , soit au moins
une valeur possible pour chaque paramètre de façon à ce que
les propriétés requises pour le système soient satisfaites et
que la réalisation physique des paramètres soit possible (pour un
robot par exemple on s'assurera que la largeur des intervalles
solutions pour
, soit au moins
une valeur possible pour chaque paramètre de façon à ce que
les propriétés requises pour le système soient satisfaites et
que la réalisation physique des paramètres soit possible (pour un
robot par exemple on s'assurera que la largeur des intervalles
solutions pour 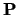 soit supérieure aux tolérances de fabrication).
soit supérieure aux tolérances de fabrication).
Même si le problème de la conception optimale est très ancien (il est mentionné par Héron d'Alexandrie), qu'il existe un corpus de littérature sur le sujet assez imposant [7] et que certains logiciels de conception utilisent la notion de contraintes22 il n'existe pas vraiment d'outils passés dans la pratique pour le résoudre. Actuellement, aucun des simulateurs mécaniques commercialisés (comme ADAMS, MesaVerde, SDS) ne propose de module de conception optimale. Nous avons déjà une forte expérience dans ce problème et nous avons développé des techniques originales de conception optimale pour des familles de mécanismes comme les robots parallèles. Par exemple, notre micro-robot MIPS (dont nous continuons le développement dans le cadre d'une ACI "Technologie de la Santé" en collaboration avec le LMARC de Besançon et le Dr. Dumond de l'hôpital Sainte Marguerite, Marseille) a bénéficié de ces techniques [17].
Un deuxième exemple: la génération automatique
de jeux de tests logiciels
Le test structurel reste encore une étape essentielle dans le
cycle
de vie du logiciel et la génération manuelle des jeux de test
est
fastidieuse et coûte cher, en particulier pour les logiciels
critiques
qui doivent satisfaire des normes (ISO, Afnor, DoD, ...) qui fixent
des
modalités de test (par exemple couverture de toutes les branches, de
tous
les n![]() uds, ...). Le respect des exigences imposées par les
organismes normatifs concernant le test représente un coût non
négligeable dans le développement des logiciels lorsque les
exigences de sécurité sont importantes.
uds, ...). Le respect des exigences imposées par les
organismes normatifs concernant le test représente un coût non
négligeable dans le développement des logiciels lorsque les
exigences de sécurité sont importantes.
La génération automatique de jeux de test est un problème difficile pour lequel il n'existe pas de solution générale (il est équivalent au problème de la terminaison d'un programme). Nous avons développé une méthode reposant sur le schéma de la programmation logique avec contraintes (PLC [8,9]) pour la génération automatique des jeux de test, c'est-à-dire la production de données d'entrée pour lesquelles un point sélectionné dans une procédure sera exécuté. Pour cela, on transforme statiquement une procédure d'un langage impératif ne contenant que des variables entières en un système de contraintes sur les domaines finis en utilisant les techniques statiques d'affectation unique (``static single assignment'') et les dépendances de contrôle du programme. La résolution du système de contraintes obtenu permet de vérifier s'il existe au moins un chemin d'exécution passant par le point choisi et permet de produire des jeux d'essais qui correspondent à l'un de ces chemins d'exécution. Le point clef de notre approche est l'utilisation des techniques de ``constraint entailment'' sur les domaines finis pour réduire l'espace de recherche et détecter très tôt certains chemins non-exécutables. Les résultats obtenus avec le premier prototype sont très encourageants.
Plus récemment, une approche analogue a été suivie par le projet Lande qui a intégré le solveur de contraintes ILOG Solver dans la méthode de génération de suites de test ``Casting'' définie dans la thèse de Lionel Van Aertryck.
Annexe: Consistances et Analyse par Intervalles
Méthodes de consistances
Un exemple de consistance locale est la Box-consistance [2]. Cette consistance peut être
expliquée intuitivement de la manière suivante: soit un
système de
contraintes
Il existe de nombreuses manières d'implanter un filtrage par
box-consistance. Une manière triviale consiste à déterminer
les
intervalles à gauche et à droite ![]() de l'intervalle
initial pouvant contenir des solutions du système: l'intervalle
initial est alors remplacé par l'intervalle
de l'intervalle
initial pouvant contenir des solutions du système: l'intervalle
initial est alors remplacé par l'intervalle
![]() . La détermination de
. La détermination de ![]() se fait
à
partir de l'intervalle initial
se fait
à
partir de l'intervalle initial ![]() on procédant par dichotomie
sur
les intervalles
on procédant par dichotomie
sur
les intervalles ![]() et
et ![]() et en arrêtant le
processus lorsque la largeur de l'intervalle est inférieure à un
seuil
donné. Par exemple, considérons la contrainte
et en arrêtant le
processus lorsque la largeur de l'intervalle est inférieure à un
seuil
donné. Par exemple, considérons la contrainte
![]() pour
pour
![]() dans l'intervalle [2,4].
La détermination de
dans l'intervalle [2,4].
La détermination de ![]() se fait en
considérant l'intervalle [3,4]: comme
se fait en
considérant l'intervalle [3,4]: comme ![]() =[2,11]
l'intervalle
est éliminé. On poursuit alors par le calcul
de
=[2,11]
l'intervalle
est éliminé. On poursuit alors par le calcul
de ![]() à partir de l'intervalle [2,3]: comme
à partir de l'intervalle [2,3]: comme
![]() =[-1,6] l'intervalle n'est pas réduit et on
considère l'intervalle [2,2.5]. La détermination de
=[-1,6] l'intervalle n'est pas réduit et on
considère l'intervalle [2,2.5]. La détermination de ![]() suit
donc la
progression suivante:
suit
donc la
progression suivante:
![\begin{eqnarray*}
f([2,2.5])=[0,3.25] && \Rightarrow L=[2,3] \\
f([2,2.25])=[0....
...=[2.25,3]\\
f([2.25,3])=[0.0625,5.5] && \Rightarrow x=\emptyset
\end{eqnarray*}](img72.png)
Ainsi avec 5 évaluations de la fonction, on a réussi à déterminer que l'intervalle [2,4] ne contient pas de zéro de
Un exemple de consistance non-locale est la 3B-consistance [16] qui consiste à vérifier si le
système de contraintes ne devient pas inconsistant lorsque
l'intervalle pour une variable est remplacé successivement par un
intervalle réduit contenant soit la borne gauche ou droite de
l'intervalle initial. Ainsi si ![]() est un système de contraintes
contenant la variable
est un système de contraintes
contenant la variable ![]() dont l'intervalle est
dont l'intervalle est ![]() on
vérifie si le système peut être satisfait lorsque
on
vérifie si le système peut être satisfait lorsque ![]() est
dans l'intervalle
est
dans l'intervalle
![]() : si ce n'est pas
le cas alors la portion
: si ce n'est pas
le cas alors la portion
![]() de
de ![]() est éliminée et le filtrage se poursuit sur
l'intervalle
est éliminée et le filtrage se poursuit sur
l'intervalle
![]() ; sinon le filtrage se poursuit avec
l'intervalle
; sinon le filtrage se poursuit avec
l'intervalle
![]() et ainsi de suite jusqu'à ce que la largeur de
l'intervalle considéré soit inférieure à un certain seuil.
On
procédera de même pour la portion droite de l'intervalle de
départ.
et ainsi de suite jusqu'à ce que la largeur de
l'intervalle considéré soit inférieure à un certain seuil.
On
procédera de même pour la portion droite de l'intervalle de
départ.
Prenons par exemple les contraintes
![]() pour
pour ![]() et
et ![]() dans
l'intervalle [-100,100]. Pour la 3B-consistance à gauche on
examinera ces deux contraintes pour
dans
l'intervalle [-100,100]. Pour la 3B-consistance à gauche on
examinera ces deux contraintes pour ![]() dans [-100,0].
On appliquera la 2B-consistance (voir section 2.2.2)
au système où
le domaine de
dans [-100,0].
On appliquera la 2B-consistance (voir section 2.2.2)
au système où
le domaine de ![]() est réduit à [-100,0] pour essayer
d'éliminer cette portion d'intervalle. Dans ce cas précis,
on arrivera ainsi à réduire les domaines de
est réduit à [-100,0] pour essayer
d'éliminer cette portion d'intervalle. Dans ce cas précis,
on arrivera ainsi à réduire les domaines de ![]() et de
et de ![]() à l'intervalle
à l'intervalle
![]() .
Le point important est que la modification du domaine de
.
Le point important est que la modification du domaine de ![]() est appliquée simultanément à l'ensemble des contraintes
(contrairement
à la box-consistance qui n'applique de telles modifications qu'à une
seule contrainte).
est appliquée simultanément à l'ensemble des contraintes
(contrairement
à la box-consistance qui n'applique de telles modifications qu'à une
seule contrainte).
Comme on peut le voir sur ces quelques exemples, il existe de nombreuses méthodes de consistance. Leur efficacité peut se mesurer selon deux critères:
- l'importance de la réduction des
intervalles qu'elles provoquent. On notera
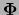 le filtrage obtenu
et pour deux méthodes
le filtrage obtenu
et pour deux méthodes 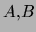 la notation
la notation
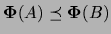 indiquera que la méthode
indiquera que la méthode 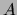 provoquera une
réduction au moins égale à la méthode
provoquera une
réduction au moins égale à la méthode 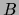
- le coût en calcul des méthodes.
Il existe des résultats théoriques sur le premier
point [4]: par exemple, pour les méthodes de Box
consistance et 2B (voir section 2.2.2)
il a pu être établi que:
Le second critère quant à lui est beaucoup plus difficile à mesurer. Si la Box-consistance est à priori plus rétractante que la 2B-consistance, nous avons vu que pour
Analyse par Intervalles
Il existe aussi une multitude de techniques qui permettent
d'améliorer
sensiblement l'efficacité de la méthode de dichotomie de base. On
peut
distinguer grossièrement quatre types de méthodes numériques:
- amélioration de l'évaluation, par exemple en utilisant la monotonie de la fonction ou par une réécriture. La monotonie consiste à calculer une évaluation par intervalles des gradients des contraintes. Si un de ces gradients ne contient pas 0 la fonction est monotone localement ce qui permet de calculer exactement les bornes. Ce processus est récursif (remplacer l'intervalle pour une inconnue par une valeur peut amener l'intervalle d'un autre gradient à ne plus contenir 0) et peut se faire sur des dérivées d'ordre plus élevé,
- utilisation d'un opérateur rétractant qui permette de réduire sensiblement la largeur des intervalles de départ (par exemple méthode de Newton par intervalles [28]),
- utilisation de tests qui garantissent l'unicité du zéro dans un intervalle donné ou qui permettent de calculer un tel intervalle, et fournissant un schéma numérique permettant de déterminer le zéro: test de Moore [22] pour l'opérateur de Krawczyk [15] ou test de Kantorovitch [34], pour le schéma de Newton,
- utilisation d'opérateur d'exclusion: ces opérateurs permettent d'affirmer qu'il n'existe pas de racines dans un intervalle donné [6].
Une parallélisation logicielle permet aussi d'améliorer de manière importante l'efficacité des algorithmes: elle repose sur le fait que dans les algorithmes on examine le comportement d'éléments d'une liste d'intervalles, examen qui ne dépend que de l'élément et pas des autres éléments de la liste et qui peut donc être traité dans le cadre d'une implantation distribuée.
Annexe: Limitations de la programmation par contraintes
Sensibilité de l'efficacité
La plupart des classes de problèmes de satisfaction de contraintes sont NP-complètes. Comme pour beaucoup de méthodes s'attaquant à ce type de problème, l'efficacité d'une approche par contraintes est difficilement prédictible. Le temps de résolution est très sensible:
- aux données d'entrée: un changement, même modeste, sur une contrainte ou sur les bornes d'une inconnue peut parfois avoir des effets très importants,
- aux choix des méthodes employées: comme nous l'avons vu, il existe une grande diversité de méthodes pour la résolution de problèmes de contraintes. Ainsi, pour les contraintes sur les domaines finis, un point critique réside dans le choix des niveaux de filtrage et des stratégies de recherche. Dans de nombreuses applications sur les domaines continus, l'efficacité de la résolution dépend du type de filtrage (voir section 2.2.2) voire du mode de combinaison de ces filtrages [4,10]. Pour le moment, ces choix sont presque exclusivement basés sur la forme syntaxique des contraintes et les performances sont peu prédictibles; des expérimentations sur différentes instances d'un problème sont souvent nécessaires pour identifier la meilleure approche en termes de performances.
- aux valeurs des paramètres utilisés dans les méthodes: par exemple une méthode comme la 3B peut présenter une convergence asymptotique lente et la valeur du paramètre qui définit l'arrêt de l'utilisation de la 3B et le passage à la bissection va jouer un rôle-clé dans l'efficacité de la résolution.
Les interfaces
Actuellement, la plupart des logiciels de satisfaction de contraintes sont soit des extensions de langages de programmation (CLP), soit des bibliothèques qui utilisent des langages de programmation conventionnels (comme dans ILOG Solver23, CHIP24, Prolog IV25Declic26). À un autre bout du spectre, il existe des logiciels comme Numerica [37] ou OPL [36] qui permettent de simplifier la description des contraintes ou de modéliser visuellement un problème de contraintes, ce qui permet à la fois de générer un programme de résolution et d'en examiner le déroulement pour en identifier les faiblesses (VisOpt VML27). Dans tous les cas l'utilisation de ce type d'outils nécessite le passage par une phase intermédiaire (création de code ou portage dans un symbolisme particulier) qui est lourde pour l'utilisateur.
Annexe: Axe méthodes de résolution
Consistance et analyse par intervalles: les
méthodes
hybrides
Participants: J-P. Merlet, B. Neveu, Y. Papegay, M. Rueher, G. Trombettoni
Même si l'objet en est le même, les techniques utilisant la consistance diffèrent sensiblement des techniques de l'analyse par intervalles, plus proches de l'analyse numérique. Il est clair que l'efficacité des algorithmes ne pourrait qu'être améliorée en utilisant une algorithmique hybride mêlant les deux approches, complétée éventuellement par du calcul formel, profitant ainsi de la complémentarité des partenaires du projet.
Dans une approche hybride, une procédure de résolution se déroule selon les étapes suivantes:
- choix d'une variable de bissection,
- bissection: les 2 nouvelles boîtes créés sont alors soumises
à :
- des opérateurs rétractants: ces opérateurs permettront éventuellement de réduire la taille des intervalles de la boîte, voire de déterminer qu'il n'y a pas de solution dans la boîte. Ce filtrage peut être local (on ne considère qu'une équation à la fois), par exemple en appliquant la méthode 2B (2.2.2), ou non locale, par exemple en utilisant la méthode 3B (7), la méthode de Newton par intervalles ou la méthode du simplexe (9.2),
- des opérateurs d'exclusion: ces opérateurs permettent de prouver qu'il n'existe pas de solution dans la boîte. L'opérateur de ce type le plus simple est celui dans lequel on évalue les équations en terme d'intervalles pour vérifier si 0 est une valeur possible pour l'équation,
- des opérateurs d'existence et d'unicité: ces opérateurs permettent de déterminer qu'il existe une solution unique dans la boîte et sont associés à une méthode numérique qui permet de la déterminer de manière garantie (test de Moore ou de Kantorovitch par exemple, voir section 7.2)
- que la boîte n'est pas réduite
- qu'un ou plusieurs des intervalles de la boîte ont une taille réduite
- qu'une solution unique est trouvée dans la boîte
- qu'il est prouvé que la boîte ne contient pas de solution
- stockage des boîtes issues du filtrage dans la liste des boîtes à traiter
- traitement de la nouvelle boîte courante
L'intérêt d'une approche hybride a été illustré par le projet ESPRIT CHIC-2 qui s'est terminé en 1999 et dont les partenaires industriels étaient Renault, Bouygues, ICL et Eurodecision et par la création d'un groupe de travail sur le thème des contraintes au sein de l'ERCIM. Nos objectifs sont donc les suivants:
- une implantation systématique des algorithmes de consistance et d'analyse par intervalles dans le cadre de la plate-forme logicielle générique (voir section 5.7)
- le développement de nouvelles méthodes (voir les deux sections suivantes)
- une analyse expérimentale dont les résultats seront stockés dans une base de cas
- l'utilisation systématique du calcul formel pour
- faciliter l'utilisation des méthodes de résolution
- profiter de certaines facilités qu'il permet pour une utilisation systématique des méthodes de consistance reposant sur l'écriture des fonctions (méthode 2B par exemple)
- profiter éventuellement des possibilités de calcul exact qui existe dans ce domaine
Solveurs spécifiques
Participants: J-P. Merlet, Y. Papegay, G. Trombettoni, M. Rueher
La prise en compte des spécificités de la structure des systèmes à résoudre peut permettre de développer des algorithmes plus efficaces, le gain en performance pouvant être très important même pour une perte de généricité faible.
Système à équations partiellement linéaires
Le premier système spécifique que nous avons considéré est
celui où
certaines équations peuvent
s'écrire
sous la forme:
où
Système d'équations de distance
Un deuxième type de système spécifique que nous considérerons
est celui constitué
d'équations de distances dans un espace à ![]() dimension
qui s'écrivent sous la forme:
dimension
qui s'écrivent sous la forme:
où les
Nous avons d'ailleurs implanté une première version d'un solveur spécifique pour ce type d'équations en utilisant le fait que la structure du système permet d'apporter différentes améliorations par rapport à nos algorithmes génériques. En effet pour ce type de système:
- chaque inconnue n'apparaît au plus qu'une fois dans une équation: on peut alors montrer que les bornes fournies par l'analyse par intervalles pour l'évaluation sont exactes (il n'est donc pas nécessaire d'utiliser des techniques coûteuses d'amélioration de l'évaluation reposant sur l'utilisation des dérivées)
- la 2B-consistance est mise en
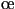 uvre de manière
systématique. Pour chaque équation, chaque terme carré
uvre de manière
systématique. Pour chaque équation, chaque terme carré
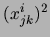 est évalué comme
est évalué comme
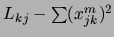 ,
,
![$m\not=i,
m\in[1,n]$](img101.png) (conduisant à l'intervalle
(conduisant à l'intervalle 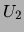 ).
Si
).
Si
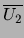 est négatif alors l'équation n'admet pas de
racine. Si
est négatif alors l'équation n'admet pas de
racine. Si
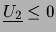 l'intervalle pour l'inconnue
l'intervalle pour l'inconnue 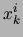 , en entrée égal
à
, en entrée égal
à 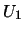 , est calculé comme
, est calculé comme
![$U_1 \cap [\underline{x^i_j}-\sqrt{\overline{U_2}},
\overline{x^i_j}+\sqrt{\overline{U_2}}]$](img106.png) . Si
. Si
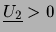 alors
alors  peut appartenir soit à l'intervalle
peut appartenir soit à l'intervalle
![$[\underline{x^i_j}-\sqrt{\overline{U_2}},
\overline{x^i_j}-\sqrt{\underline{U_2}}]$](img109.png) soit à
soit à
![$[\overline{x^i_j}+\sqrt{\underline{U_2}},
\overline{x^i_j}+\sqrt{\overline{U_2}}]$](img110.png) . La prise en compte de ces
contraintes permet
soit d'améliorer l'intervalle pour
. La prise en compte de ces
contraintes permet
soit d'améliorer l'intervalle pour 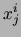 , soit de rejeter la
boîte courante,
, soit de rejeter la
boîte courante,
- nous avons pu construire une version plus "forte" du test de Kantorovitch (la largeur des intervalles dans lesquels on assure l'existence d'une solution unique est largement plus grande que dans la version générale), tout en réduisant le nombre d'opérations nécessaire à ce calcul (par exemple la matrice Hessienne est une matrice constante qui n'est calculée qu'une fois),
- l'évaluation exacte des bornes pour les équations permet
une mise en
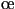 uvre efficace de la méthode 3B, même si nous
estimons que l'on pourrait développer une 3B spécifique encore plus
efficace,
uvre efficace de la méthode 3B, même si nous
estimons que l'on pourrait développer une 3B spécifique encore plus
efficace,
- pour chaque boîte nous utilisons un schéma de Newton classique avec un nombre limité d'itérations. Si la méthode de Newton converge vers une solution non encore déterminée nous procédons alors à une inflation de la solution c'est-à-dire que nous calculons un intervalle contenant la solution, et uniquement celle-ci, en utilisant une méthode classique en analyse par intervalles [23] mais qui a été adaptée aux équations traitées On recherche ensuite dans la liste des boîtes à traiter s'il en existe une contenant cette solution et si c'est le cas on la modifie pour que la solution en soit exclue,
- nous procédons au changement
de variable
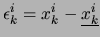 :
les équations
initiales se transforment en équations avec une partie linéaire
dans les
:
les équations
initiales se transforment en équations avec une partie linéaire
dans les 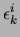 et une partie non linéaire dans les mêmes
inconnues. La méthode de Yamamura,
décrite dans
le paragraphe précédent, peut alors être utilisée.
et une partie non linéaire dans les mêmes
inconnues. La méthode de Yamamura,
décrite dans
le paragraphe précédent, peut alors être utilisée.
Il faut noter que ce solveur a été utilisé récemment avec une très bonne efficacité pour deux autres problèmes réputés difficiles: pour l'analyse géométrique de suspension de mécanisme [26] (système de 19 équations) ainsi que pour la détermination de la structure 3D d'une molécule d'une centaine d'atomes (système d'environ 400 équations).
Solveurs pour les équations trigonométriques
Un autre type de système spécifique qui nous intéresse
est celui des systèmes trigonométriques ou algébro-trigonométriques (les inconnues n'interviennent que via
des fonctions algébriques ou trigonométriques).
Comme la
dépendance
des fonctions trigonométriques est ignorée
dans les évaluations
seule une phase de décomposition sémantique
permet de la prendre en compte et
d'améliorer l'évaluation par intervalles des
contraintes (par exemple des termes de types
![]() , où
, où ![]() et
et ![]() sont des réels seront
évalués globalement plutôt que terme par terme). Nous avons
d'ailleurs déjà entamé ce travail dans
le cadre
d'une collaboration interne. Le projet MIAOU, dans le cadre d'un
contrat avec le CNES, devait déterminer l'ensemble des solutions
d'un système d'équations trigonométriques
et ne trouvait pas de méthode de résolution satisfaisante.
Nous avons alors proposé une méthode reposant sur
une adaptation mineure d'un de nos
algorithmes et utilisant, pour la détermination des intervalles de
départ, des
informations sur la géométrie des solutions fournies par
l'action GALAAD. Cette méthode
a été intégrée dans une chaîne logicielle
fournie par MIAOU au CNES.
sont des réels seront
évalués globalement plutôt que terme par terme). Nous avons
d'ailleurs déjà entamé ce travail dans
le cadre
d'une collaboration interne. Le projet MIAOU, dans le cadre d'un
contrat avec le CNES, devait déterminer l'ensemble des solutions
d'un système d'équations trigonométriques
et ne trouvait pas de méthode de résolution satisfaisante.
Nous avons alors proposé une méthode reposant sur
une adaptation mineure d'un de nos
algorithmes et utilisant, pour la détermination des intervalles de
départ, des
informations sur la géométrie des solutions fournies par
l'action GALAAD. Cette méthode
a été intégrée dans une chaîne logicielle
fournie par MIAOU au CNES.
Collaboration entre solveurs
Participants: M. Rueher
Comme nous l'avons vu,
il existe de nombreuses variantes des solveurs de base ainsi que de
multiples méthodes qui permettent d'en améliorer l'efficacité.
Dans le cadre de ce projet, nous étudierons les méthodes de
résolution reposant sur la collaboration entre différents
solveurs. Il s'agit ici de définir les modes de communication et
d'échanges de données qui autorisent une mise en ![]() uvre
efficace de différents algorithmes et techniques pour la
résolution d'un même problème.
uvre
efficace de différents algorithmes et techniques pour la
résolution d'un même problème.
Ce travail a été initié dans le projet Contraintes de l'I3S avec la définition de deux principaux modes de collaboration entre solveurs pour la résolution de contraintes sur les réels, modes qui ont permis de résoudre des problèmes qu'aucun des solveurs ne pouvait traiter isolément.
- Un premier modèle de coopération entre solveurs
symboliques
et numériques a été défini, basé sur la notion d'acteurs
communiquant de manière asynchrone via des messages ``ask'' et
``tell''; le système prototype intègre un
solveur d'équations polynomiales,
un solveur
d'équations et d'inéquations linéaires et un système de
propagation d'intervalles.
- Un deuxième modèle a abouti au
logiciel CCC faisant coopérer un
solveur
reposant sur la notion de consistance et un solveur de contraintes
linéaires [32]. Une difficulté majeure dans le mode
de communication ci-dessus
est la prise en compte au
plus tôt par chaque solveur des résultats pertinents des autres
solveurs. C'est pourquoi nous avons introduit un modèle de
coopération reposant sur une communication ``fine'' entre des
solveurs
travaillant de manière concurrente sur un même ensemble de
contraintes.
Des processus concurrents mettent à jour les contraintes
traitées
par les solveurs,
l'idée de base étant d'éviter les convergences asymptotiques
lentes
en introduisant en cours de calcul de nouvelles contraintes issues
du
solveur linéaire.
Annexe: Axe outils pour les méthodes de résolution
Techniques de filtrage
Participants:H. Collavizza, B. Neveu, Y. Papegay, M. Rueher, G. Trombettoni
Les techniques de filtrage utilisent des algorithmes
polynomiaux pour réduire de manière significative l'espace de
recherche. Ces techniques, initialement développées pour les
CSP
sur les domaines finis,
consistent
à relaxer le problème initial en un ensemble de problèmes qui
sont
plus faciles à résoudre. Par exemple, sur les domaines finis, on
va considérer chaque contrainte séparément et éliminer de
l'ensemble des valeurs acceptables pour une variable les valeurs
incompatibles avec cette contrainte, ce qui permet par la suite de
considérer le problème dans sa globalité à partir d'un
domaine
de recherche très restreint. Un exemple pratique peut être
donné
pour le calcul de la géométrie d'un robot dont
l'espace de travail doit contenir un objet ![]() défini à l'avance: dans un premier temps, on recherchera
seulement
les valeurs
possibles des paramètres géométriques telles que l'espace de
travail du robot contienne quelques points particuliers
caractéristiques de
défini à l'avance: dans un premier temps, on recherchera
seulement
les valeurs
possibles des paramètres géométriques telles que l'espace de
travail du robot contienne quelques points particuliers
caractéristiques de ![]() .
.
La spécialisation du problème en diminue notablement la complexité et les techniques de propagation de contraintes permettent d'obtenir l'ensemble des valeurs possibles des paramètres géométriques sous la forme d'une liste d'intervalles où chaque élément à une taille réduite. Pour chaque élément de cette liste on peut alors déterminer s'il existe un sous ensemble d'intervalles solution du problème global.
Une autre approche du filtrage consiste à développer des
algorithmes efficaces pour résoudre globalement un sous-ensemble
de
contraintes spécifiques. L'idée consiste ici à s'intéresser
à un sous-ensemble homogène de contraintes qui peuvent
être résolues par des algorithmes polynomiaux.
En domaine fini des contributions sont décrites à la
section 3.3, mais il semble également très prometteur de
mettre en ![]() uvre cette approche en propagation d'intervalles sur
les domaines continus.
uvre cette approche en propagation d'intervalles sur
les domaines continus.
Une autre axe de recherche est l'utilisation des outils du calcul
formel pour la mise en ![]() uvre systématique de certaines méthodes
de consistance comme la 2B par exemple.
uvre systématique de certaines méthodes
de consistance comme la 2B par exemple.
Choix des variables de bissection
Participants: J-P. Merlet, B. Neveu, M. Rueher, G. Trombettoni
Dans le processus de bissection on ne coupe, en général, qu'une variable à la fois. Il se pose alors le problème du choix de la variable à couper. Différentes heuristiques ont été proposées:
- couper la variable dont l'intervalle est le plus large (ce qui est peu efficace pour les systèmes mal conditionnés),
- couper en round-robin, c'est-à-dire que chaque variable est choisie à tour de rôle [37],
- choisir la variable dont l'évaluation du gradient pondérée par la largeur de l'intervalle de la variable est le plus grand, l'idée étant de couper la variable qui semble avoir le plus d'influence sur une contrainte (smear function de Kearfott [14])
Une autre approche consiste à couper l'ensemble des variables d'un sous-ensemble des inconnues, ceci en fonction de la structure du système, ce que nous expliciterons dans la section 10.3.
Le choix de la méthode de bissection joue évidemment un rôle important dans l'efficacité des méthodes mais il est difficile d'estimer a priori quelle est celle qui est la plus appropriée à un problème donné. Nous nous attacherons à une étude théorique de ce point en nous restreignant à des classes particulières de problèmes.
Techniques de décomposition
Participants: B. Neveu, G. Trombettoni
Les techniques de décomposition exploitent la structure (syntaxique ou sémantique) du problème pour le décomposer en sous-problèmes indépendants ou faiblement corrélés. Un exemple typique de l'utilisation de la décomposition est le problème de la recherche des conformations de molécules de grande taille où l'on cherche tout d'abord à résoudre un ensemble de contraintes associées à des sous-structures indépendantes ou très faiblement dépendantes (par exemple une arborescence attachée à la structure globale en un seul point).
Nous étudions un nouvel algorithme de décomposition reposant
sur une analyse du graphe de contraintes. Après une
décomposition grossière du graphe de contraintes reposant sur
les
travaux de Dulmage et Mendelsohn, cet algorithme produit une
décomposition fine du graphe en ``petits'' blocs (c.a.d. un graphe
orienté sans circuit de sous-systèmes d'équations). Chaque
bloc
est résolu par un solveur capable de trouver toutes les
solutions (Numerica) et un mécanisme de retour en arrière,
adaptation d'un
algorithme de retour en arrière issu du domaine des contraintes
discrètes, est mis en ![]() uvre lorsque aucune solution n'est
trouvée. Les premiers résultats produits par un prototype en
C++
sur de petits problèmes d'assemblage mécanique sont très
encourageants [3].
On peut considérer la décomposition obtenue
comme
une heuristique de choix de la variable à bissecter pour le
solveur utilisant les intervalles (voir section 10.2).
uvre lorsque aucune solution n'est
trouvée. Les premiers résultats produits par un prototype en
C++
sur de petits problèmes d'assemblage mécanique sont très
encourageants [3].
On peut considérer la décomposition obtenue
comme
une heuristique de choix de la variable à bissecter pour le
solveur utilisant les intervalles (voir section 10.2).
Nous nous intéressons aussi aux techniques de décomposition qui utilise la détection de rigidités dans un système géométrique. C'est un problème bien connu et étudié par différentes communautés, comme la CAO, la théorie des mécanismes ou la topologie structurelle. C'est donc naturellement un sujet pour lequel la complémentarité des équipes à l'origine de COPRIN va jouer à plein pour développer une recherche combinant les résultats de différentes communautés.
L'équipe de l'I3S Contraintes a abordé ce problème dans l'optique de
concevoir une brique de base pour
un nouvel outil de CAO. Elle a étudié les algorithmes de
rigidification récursive proposés par les chercheurs en CAO.
L'aspect
opérationnel et constructif de cette approche ainsi que les
techniques
de flot récemment employées pour la mettre en ![]() uvre sont
originaux mais elle doit être complétée par une
analyse
géométrique qui pourrait être fournie
par la
topologie structurelle et la théorie des mécanismes.
uvre sont
originaux mais elle doit être complétée par une
analyse
géométrique qui pourrait être fournie
par la
topologie structurelle et la théorie des mécanismes.
Notons que ce problème pourrait avoir aussi une application en
vision par ordinateur dans le domaine de la reconstruction 3D où
des éléments géométriques (lignes, plans) doivent respecter des
contraintes géométriques (perpendicularité, parallélisme, ![]() ).
Ici la détermination de
la rigidité peut permettre de limiter le nombre d'éléments à
apparier dans chaque image ou de donner des indications sur la
nature
des éléments à introduire dans le processus pour aboutir à
une
structure rigide.
).
Ici la détermination de
la rigidité peut permettre de limiter le nombre d'éléments à
apparier dans chaque image ou de donner des indications sur la
nature
des éléments à introduire dans le processus pour aboutir à
une
structure rigide.
Nous nous intéressons aussi à la décomposition reposant sur
une analyse des
contraintes fonctionnelles et des contraintes
géométriques en cherchant à modéliser les constructions
à
la
règle et au compas utilisées en géométrie.
Le modèle des contraintes fonctionnelles est un modèle très
simple utilisé dans le domaine des interfaces graphiques.
Il permet le
rétablissement de la cohérence lors de l'ajout interactif de
nouvelles contraintes sous réserve de disposer de méthodes
permettant de garantir individuellement les contraintes.
Nous étudions un nouvel
algorithme [35] capable de
prendre en compte simultanément plusieurs contraintes pour
rétablir cette cohérence, ce qui ouvre
des perspectives pour
l'édition "intelligente" de dessins (voir section ![[*]](crossref.png) ).
).
Une voie plus prospective concerne l'analyse dynamique de la structure du graphe de contraintes c'est-à-dire pendant la résolution. En effet, une structure particulière peut apparaître quand une partie du problème est déjà résolue et que certaines variables sont instanciées. Nous voulons concevoir des algorithmes capables de ``capter'' la structure d'un problème tout en préservant les acquis des solveurs existants, à savoir l'établissement de cohérences partielles pendant la résolution et la prise en compte de contraintes globales.
Recherche arborescente
Participants: J-P. Merlet, B. Neveu, G. Trombettoni
Les méthodes de recherche arborescente classiques en profondeur d'abord pour la résolution de contraintes doivent essentiellement choisir le prochain point de choix (choix de variable) et la prochaine branche à explorer en premier (choix de valeur). Leur efficacité est très dépendante des premiers choix effectués en haut de l'arbre. Pour pallier cette difficulté, d'autres algorithmes ont été conçus comme d'une part la recherche à divergence limitée (LDS) [12] dont le parcours repose sur une limitation des divergences par rapport aux choix de l'heuristique et d'autre part la recherche entrelacée (IDFS) [21] qui crée au départ plusieurs sous-arbres et alterne l'exploration de ces sous-arbres.
Dans le cadre de ces méthodes, nous étudions une nouvelle heuristique de choix de valeur dynamique qui évolue au cours de la recherche et l'avons incorporée dans l'algorithme LDS. Cela a amené à concevoir un algorithme où, quand on obtient une solution partielle de taille supérieure à la solution partielle courante, la recherche se recentre autour de cette nouvelle solution partielle. On atteint ainsi les limites de la recherche arborescente et on se rapproche des algorithmes de recherche locale à voisinages étendus.
Nous avons également conçu un nouvel algorithme nommé recherche à focalisation progressive (PFS), qui commence comme la recherche entrelacée IDFS et petit à petit se focalise vers les sous-arbres les plus prometteurs. Un modèle théorique a également été proposé [27] pour étudier la pertinence des nouvelles méthodes de recherche entrelacée et à divergence limitée.
Un autre algorithme manipule une base de ``nogoods'' (c.a.d. instanciations qui entraînent un échec) de taille polynomiale et permet d'éviter ainsi l'exploration de sous-arbres identiques sans solution. Des algorithmes similaires sont disponibles dans ILOG Solver et donnent des résultats positifs dans certaines applications. Nous souhaitons approfondir cet axe de recherche pour améliorer les techniques sous-jacentes et mieux déterminer les niches d'application de ces différents algorithmes.
Annexe: Axe données, optimisation et type de solutions
Données
Participants: J-P. Merlet, Y. Papegay
L'intérêt évident de l'arithmétique d'intervalles est de
permettre à priori le traitement de n'importe quelle fonction ayant
une forme analytique. Il sera aussi possible, parfois avec plus de
difficulté, de gérer les cas où la fonction est définie par un
processus opératoire avec des problèmes proches de
nos recherche en génération de jeux de tests
logiciels, section 12.1. Mais l'utilisation des intervalles
nécessitera une transcription de la fonction dans un langage de
programmation approprié. Cette transcription peut être rapidement
fastidieuse: ici le calcul formel va jouer un rôle essentiel
d'interface pour l'écriture de code, pour une mise en forme optimale
des expressions (l'évaluation par intervalles dépend en effet de
l'écriture des fonctions) ainsi que pour la mise en ![]() uvre
automatique de certaines consistances comme la 2B.
De même, le calcul formel peut permettre d'aider à gérer des cas,
comme le calcul de déterminant de matrices,
où l'obtention d'une forme analytique complète n'est pas
souhaitable (ou possible) de par sa complexité, en permettant
d'obtenir des résultats intermédiaires simplifiés, résultats
qui seront utilisés pour obtenir finalement un processus
d'évaluation par intervalles.
uvre
automatique de certaines consistances comme la 2B.
De même, le calcul formel peut permettre d'aider à gérer des cas,
comme le calcul de déterminant de matrices,
où l'obtention d'une forme analytique complète n'est pas
souhaitable (ou possible) de par sa complexité, en permettant
d'obtenir des résultats intermédiaires simplifiés, résultats
qui seront utilisés pour obtenir finalement un processus
d'évaluation par intervalles.
Optimisation
Participants: J-P. Merlet, B. Neveu, M. Rueher
La programmation par contraintes est un outil approprié pour résoudre des problèmes d'optimisation en particulier si l'on veut une garantie sur le caractère global du résultat et que le problème est soumis à des contraintes complexes. De nombreuses équipes travaillent sur ce problème mais nous nous attacherons à la résolution de problèmes particuliers d'optimisation:
- les problèmes où le calcul exact des extrémums n'a pas de
caractère
impératif mais où certaines propriétés sur ces extréma
doivent
être prouvées
(par exemple prouver le
passage par zéro d'une fonctionnelle
ou que l'écart entre minimum et maximum
dépasse un seuil),
- les problèmes mêlant domaines continus et domaines discrets: ce sont des cas très importants dans la pratique, par exemple s'il n'existe qu'un choix limité pour certaines grandeurs physiques alors que d'autres évoluent dans un domaine continu.
Pour résoudre des problèmes d'optimisation, dans le domaine discret, l'approche qui a eu le plus de succès dans la communauté ``contraintes'' repose sur la définition de nouvelles contraintes globales qui englobent la fonction objectif et un sous-ensemble homogène de contraintes du problème [1,24,29,33]. Dans ce cas, les algorithmes polynomiaux associés aux contraintes globales évitent de refaire plusieurs fois un travail quasi-identique pour chaque problème de décision et permettent de propager les effets des réductions de bornes.
C'est une voie que nous avons explorée pour des
problèmes
dont la fonction objectif est définie par ![]() et où les variables
et où les variables ![]() sont sujettes à des contraintes
du type:
sont sujettes à des contraintes
du type: ![]() . Un algorithme polynomial
a été proposé pour
éliminer des valeurs des domaines des variables [30].
Cette voie sera explorée pour le domaine
continu.
. Un algorithme polynomial
a été proposé pour
éliminer des valeurs des domaines des variables [30].
Cette voie sera explorée pour le domaine
continu.
Type de solutions
Participants: J-P. Merlet, B. Neveu, M. Rueher
Un point d'intérêt commun est la détermination de boîtes où le système est totalement consistant, c'est-à-dire que tous les points de la boîte sont solutions (mais des solutions peuvent exister en dehors de ces boîtes) alors que les consistances partielles définissent une boîte "extérieure" qui contient toutes les solutions mais dont un certain nombre de points ne sont pas solutions. En effet, dans de nombreuses applications (comme, par exemple, la conception optimale), l'utilisateur souhaite plutôt connaître une boîte dont tous les points sont solutions et peut admettre que certaines boîtes solutions soient négligées (par exemple si elles sont de petite taille).
Un simple problème de balistique illustre bien ce type de
problèmes. On considère un projectile
lancé dans un champ gravitationnel uniforme ![]() , avec une
vitesse initiale
, avec une
vitesse initiale ![]() faisant un angle
faisant un angle ![]() avec le sol.
La contrainte consiste à trouver la tolérance maximale sur
avec le sol.
La contrainte consiste à trouver la tolérance maximale sur
![]() garantissant que le projectile tombe dans
un intervalle prédéfini.
Il s'agit donc de calculer le plus large intervalle possible pour
garantissant que le projectile tombe dans
un intervalle prédéfini.
Il s'agit donc de calculer le plus large intervalle possible pour
![]() (qui
ne contient pas nécessairement toutes les solutions)
tel que tous les points de l'intervalle sont
solutions.
Nous avons déjà proposé des méthodes
qui permettent de résoudre ce problème dans un cadre
restrictif [5] ou pour des applications
particulières [20]
et nous comptons les approfondir.
(qui
ne contient pas nécessairement toutes les solutions)
tel que tous les points de l'intervalle sont
solutions.
Nous avons déjà proposé des méthodes
qui permettent de résoudre ce problème dans un cadre
restrictif [5] ou pour des applications
particulières [20]
et nous comptons les approfondir.
Annexe: Domaines d'application
La génération automatique de jeux de tests
logiciels
Participants: M. Rueher
Dans le cadre d'un projet RNTL (en collaboration avec Thomson-CSF Detexis, Axlog Ingénierie, le LSR (IMAG) et le LIFC (Besançon), nous allons poursuivre nos recherches sur la génération de cas de test structurel pour des programmes C et C++ . On s'intéressera en particulier aux variables de type flottant et aux expressions évaluées sur ces variables. Nous n'avions pas inclus le traitement des flottants dans le premier prototype que nous avons réalisé à cause des difficultés suivantes:
- L'évaluation non homogène des expressions sur les flottants;
- La difficulté de garantir qu'une solution existe effectivement dans les intervalles arbitrairement petits générés par les méthodes de résolution.
- L'identification d'heuristiques de recherches efficaces pour trouver des intervalles susceptibles de contenir des solutions;
- La résolution coopérative des contraintes sur les flottants et des contraintes sur les entiers.
La théorie des mécanismes et la CAO mécanique
Participants: J-P. Merlet, G. Trombettoni, Y. PapegayC'est une source inépuisable de problèmes très divers d'optimisation, de résolutions, sur des systèmes de structures très différentes. Notre expertise dans le domaine nous permet à la fois de déterminer quels sont les problèmes et d'en moduler la complexité, mais aussi d'aller jusqu'à la validation expérimentale (parfois la seule reconnue industriellement) puisque nous participons effectivement à des développements matériels allant jusqu'à la création de nos propres robots (comme MIPS). Dans cette activité, nos travaux seront centrés sur trois thèmes majeurs:
- la conception optimale: on répond ici à une demande forte à la fois de la part des utilisateurs et des industriels de la CAO et dans le même temps on s'attaque à un problème finalement très peu étudié d'un point de vue théorique
- la CAO mécanique: Les outils de CAO actuels reposent sur des techniques qui ont peu évolué depuis 20 ans. En particulier, les relations établies pendant la conception sont "directionnelles" alors qu'une approche déclarative pourrait diminuer l'effort du concepteur. Nous étudierons l'apport des techniques d'intervalles dans ce domaine, notamment les techniques de décomposition de système de contraintes géométriques (section 10.3), de collaboration entre solveurs (section 3.1) et la certification de résultat (par exemple pour des prédicats géométriques). Des contacts préalables avec des industriels du domaine ont d'ailleurs déjà été pris. Nos objectifs sont clairs: nous ne désirons pas entamer un développement de logiciel de type Cabri ou Cinderella mais offrir des briques permettant d'en améliorer certains aspects.
- la modélisation géométrique et la calibration: c'est un point fort de nos travaux pour lequel l'analyse par intervalles a déjà fait ses preuves [13,38] avec un potentiel fort de transfert industriel.
Annexe: Positionnement par rapport aux projets INRIA
Projets à thèmes voisins
Projet ARENAIRE (Rhône-Alpes)
COPRIN fera une utilisation intensive de l'arithmétique
d'intervalles
sans que les opérations de base dans cette arithmétique et la
représentation effective de ces intervalles soient des axes de
recherche prioritaires
du projet. Toutefois, nous sommes conscients de l'impact que
peut avoir la représentation sur l'efficacité et la robustesse
des
méthodes que nous comptons développer. Dans ce cadre, il
paraît naturel
que nous suivions avec attention les développements que propose ce
projet sur l'arithmétique exacte ou précise. Ce sera en
particulier le cas pour le projet MPFI
développé conjointement avec le projet SPACES.
Action CONTRAINTES (Rocquencourt)
Cette action présente trois axes principaux de recherche: langages concurrents avec contraintes, solveurs de contraintes, analyse et vérification des programmes avec deux domaines d'applications privilégiés: optimisation combinatoire et réalité virtuelle. Dans le deuxième axe qui nous concerne plus particulièrement, ce projet s'intéresse à la méthode du simplexe, à la coopération entre solveurs ainsi qu'aux contraintes dynamiques et floues avec comme objectif la synthèse de solveurs à partir de spécifications de haut niveau et l'intégration des méthodes de recherche locale et de propagation.
Nous nous distinguons de cette action par le poids important que attribuons aux méthodes hybrides, à l'adaptation des méthodes de l'analyse numérique et de la consistance à des problèmes spécifiques et par les domaines d'applications envisagés. Par contre une collaboration pourrait être instituée pour ce qui concerne la synthèse de solveurs spécifiques. Les membres de COPRIN sont d'ailleurs déjà en contact avec cette action.
Projet ESTIME (Rocquencourt)
Un des axes de recherche de ce projet est l'étude de méthodes numériques en optimisation, en particulier pour des problèmes de grande taille. Les méthodes utilisées diffèrent sensiblement d'une approche par contraintes mais il pourrait être envisagé d'adapter certaines des techniques proposées par ce projet à une approche par intervalles (par exemple, la méthode des points intérieurs devrait pouvoir être généralisée à une approche par contraintes).
Action GALAAD (Sophia-Antipolis)
Cette action issue, comme COPRIN, du projet SAGA a comme objectif
l'analyse des systèmes algébriques. Nos travaux peuvent
évidemment s'appliquer à ce thème en apportant une
stratégie nouvelle pour des systèmes algébriques à problèmes
(grande taille, coefficients approchés,
Projet IDOPT (Grenoble)
Notre intersection avec ce projet concerne la conception optimale mais la base de départ est un système d'équations différentielles, cas que nous ne considérerons pas a priori. Toutefois, si nous étions amenés à rencontrer des problèmes mixtes impliquant à la fois des équations différentielles et non différentielles, nous pourrions nous appuyer sur les travaux de ce projet.
Projet LANDE (Rennes)
La génération des jeux de test fait partie des préoccupations
du projet
Lande. Cette équipe s'intéresse tout particulièrement à la
génération
automatique de jeux de test pour des applications qui exigent un
degré
de confiance très important et justifient l'emploi de méthodes
formelles.
Le logiciel ``Casting'' utilise ainsi une spécification en B pour
générer
des jeux de test structurels.
Des contacts informels existent déjà avec des membres de cette équipe et une collaboration plus importante pourrait être développée.
Projet NUMOPT (Rhône-Alpes)
Notre intersection avec ce projet concerne les problèmes
d'optimisation. NUMOPT concentre ses recherches sur les problèmes
où les dérivées premières sont discontinues, sur l'application
de l'analyse convexe dans les
problèmes combinatoires et joue un rôle de conseil sur les
problèmes plus classiques d'optimisation pour de gros problèmes.
Il est envisagé d'établir des contacts pour les problèmes mixtes
combinatoires-continus et d'examiner comment les compétences de ce
projet pourraient être utiles pour résoudre les problèmes
particuliers d'optimisation que nous souhaitons aborder.
Projet PROTHEO (Nancy)
Le projet PROTHEO a pour but la conception et la réalisation d'outils pour la spécification et la vérification de logiciels. Dans ce cadre un des axes de recherche de ce projet a été la résolution de contraintes avec comme sous-axes l'examen de contraintes symboliques et numériques, la collaboration de solveurs, et les techniques de propagation, consistance et énumération. Toutefois une discussion avec C. Kirchner à Nancy a permis d'établir que cet axe ne faisait plus réellement partie des préoccupations du projet.
Projet SPACES (Nancy-Paris)
Ce projet est spécialisé dans le traitement des problèmes algébriques (calcul de bases de Groebner avec F8 et résolution avec RS) et dans l'implantation de structures arithmétiques performantes (bibliothèques MPFR et MPFI). Pour des raisons historiques, nous avons une relation privilégiée avec ce projet avec lequel nous collaborons de manière très régulière (co-encadrement de doctorant, contrat industriel commun, utilisation intensive de MPFR), ce qui s'est encore concrétisé récemment par l'arrivée chez SPACES comme post-doctorant d'un ancien doctorant de SAGA (D. Daney) sur un sujet présentant un intérêt commun pour SPACES et COPRIN: l'intégration d'objets MPFR comme élément de base dans le calcul portant sur les intervalles. Nous estimons d'une part que les recherches menées dans SPACES sont complémentaires de celles menées dans COPRIN et que d'autre part nous partageons avec SPACES une objectif commun avec le développement d'une approche mathématiques expérimentales où les développements théoriques s'accompagnent d'une implantation soignée et de test intensifs pour assurer la meilleure l'efficacité possible.
Mentionnons comme sujets de collaboration avec SPACES l'utilisation d'outils de ce projet pour le traitement de méthodes de consistance qui font appel en cours de processus à la résolution de systèmes algébriques ainsi que la possibilité de communication entre solveurs via le protocole udx développé dans SPACES.
Outils communs
Dans l'ensemble des projets mentionnés ci-dessus il faut mentionner que nous utiliserons à terme la bibliothèque MPFI développée conjointement par ARENAIRE et SPACES. Pour cela nous avons d'ailleurs déjà entamé une collaboration forte avec ces deux projets pour que les développements de MPFI reposent sur des structures de données qui seront compatibles avec notre plate-forme logicielle générique.
Projets avec collaboration possible ou existante
Projet MIAOU
Nous collaborons avec ce projet dans le cadre de la résolution de systèmes de contraintes trigonométriques associés à un problème de filtre HF pour le CNES. Une chaîne logicielle a été établie pour le traitement automatique de la résolution en raison de la fréquence des problèmes soumis. Nous envisageons aussi de collaborer avec ce projet pour le traitement de contraintes faisant intervenir des déterminants de matrices.
Projet ORION
Dans le cadre du projet SAGA, nous avons déjà été
confrontés au problème de la gestion de solveurs multiples et
nous avions
entamé une collaboration avec ce projet sur le pilotage
d'algorithmes.
Dans le cadre de COPRIN nous serons confrontés à une problématique
identique, avec toutefois des données de base sensiblement
différentes. Nous comptons donc poursuivre cette collaboration à
compter
du moment où notre base d'algorithmes sera suffisamment solide.
Projet PRISME
Depuis quelques années, le projet PRISME s'intéresse à la robustesse dans les calculs géométriques. A ce titre, les calculs certifiés que l'on peut faire à partir de l'analyse par intervalles sont une technique intéressante (d'ailleurs le projet utilise déjà partiellement cette technique). Nous nous proposons de collaborer avec ce projet, en particulier pour le traitement d'objets non algébriques.
Logiciels existants et en devenir
Dans les sections suivantes, nous décrivons l'existant, en commençant par les logiciels applicatifs et en terminant par les solveurs, et comment nous comptons les faire évoluer pour arriver à une structure cohérente.
Outil de visualisation graphique
Les problèmes de contraintes ont souvent une interprétation géométrique et il est donc nécessaire de disposer d'un outil ouvert pour la visualisation. Nous avons développé pour cela depuis plusieurs années un logiciel de dessins orienté géométrie, xjpdraw, actuellement diffusé dans une centaine de sites. Il est prévu d'adjoindre à ce système un module où le dessin sera défini non plus seulement par des objets géométriques mais par des contraintes géométriques (voir section 10.3 et section 3.4).
Outils de modélisation et d'analyse pour
mécanisme
Dans un domaine traditionnellement conservateur comme la mécanique, il est nécessaire de montrer par des logiciels spécifiques que le traitement des contraintes n'est pas qu'un objet de laboratoire. Pour cela, nous avons développé divers outils pour la modélisation et l'analyse de divers mécanismes (mécanisme à 4 barres, robots parallèles plans et spatiaux) qui sont utilisés pour des besoins d'enseignement ou de recherche. Même si tous intègrent peu ou prou un traitement partiel de contraintes, leur développement progressif n'a pas permis d'y inclure les algorithmes dont on sait maintenant qu'ils sont les plus efficaces. L'ensemble de ces logiciels va être revisité dans ce cadre et les nouvelles versions seront rendues disponibles par ftp anonyme.
Outil Inka de génération de jeux de test
Inka a été développé en collaboration avec Thales
``Systèmes Aéroportés''. Il s'agit d'un prototype d'un
système de génération de
jeux de test structurels. Il repose sur l'utilisation des techniques
de Constraint Entailment et de contraintes composites. Inka
comprend un module de pré-traitement qui effectue une analyse
syntaxique et qui transforme statiquement une procédure en un
système
de contraintes en utilisant les techniques statiques d'assignation
unique (forme SSA) et les dépendances de contrôle du
programme. La résolution du système de contraintes obtenu permet
de
vérifier s'il existe au moins un chemin d'exécution passant par
le
point choisi et permet de produire des jeux d'essais qui
correspondent
à l'un de ces chemins d'exécution. Le point clef de notre
approche
est l'utilisation des techniques de Constraint Entailment sur
les
domaines finis pour réduire l'espace de recherche et détecter
très tôt
certains chemins non-exécutables. Inka a été
développé sur un
sous-ensemble restreint du langage C. L'objectif de Thales
``Systèmes Aéroportés'' est de
développer à partir de Inka un produit opérationnel pour
le
langage C++ et de le commercialiser.
Solveurs
ALIAS (analyse par intervalles et consistances)
La bibliothèque ALIAS (Algorithms Library of Interval Analysis for Systems )29 a pour objet d'appliquer l'analyse par intervalles au problèmes d'analyse et de résolution des systèmes composés d'équations et d'inégalités.
ALIAS repose pour les opérations de base de l'analyse par intervalles sur le logiciel BIAS/Profil et offre actuellement les fonctionnalités suivantes :
- algorithmes de résolution pour les systèmes de dimension 0, avec dans une certaine mesure, la possibilité de résoudre des systèmes ayant des intervalles comme coefficients,
- algorithmes de résolution approximative pour les systèmes de dimension positive,
- algorithme d'optimisation globale,
- analyse d'équations algébriques et trigonométriques permettant de déterminer des bornes sur les racines ou le nombre de racines dans un intervalle donné sans passer par la résolution. Les coefficients des équations peuvent être des intervalles,
- un ``parser'' pour l'évaluation de formules par analyse par intervalles [18] écrite de manière analytique dans un fichier. Ce parser est très utile dans le cas où le traitement d'un problème est générique quelles que soient les équations en entrée puisqu'il permet de traiter sans développement de code un ensemble de problèmes par simple modification du fichier d'équations.
Les méthodes de résolution d'ALIAS sont partiellement interfacées pour pouvoir être utilisées directement à partir de MAPLE.
Le but premier de cette interface est de créer automatiquement le code C++ correspondant au problème à traiter, de le compiler, puis de l'exécuter pour finalement récupérer sous MAPLE le résultat du traitement. Mais les capacités de MAPLE sont aussi utilisées pour quatre autres objectifs:
- analyse sémantique: par exemple pour créer automatiquement
un code C++ permettant la mise en
 uvre de la consistance 2B,
uvre de la consistance 2B,
- mise en forme des expressions: avant écriture du code C++ les expressions qui devront être évaluées avec l'arithmétique d'intervalle sont mises sous une forme compacte qui permet à la fois de réduire le temps de calcul de l'évaluation et souvent d'en améliorer les bornes,
- calcul de l'espace de recherche: pour certains systèmes particuliers, comme les équations de distance, MAPLE est utilisé pour déterminer la boîte initiale qui contient l'ensemble des solutions,
- calcul des solutions avec une précision arbitraire: dans certains cas, le code C++ produit des boîtes contenant de manière garantie une, et une seule, solution du problème. De plus est associé à chacune de ces solutions une procédure numérique à convergence garantie (par exemple le schéma de Newton) qui permet de calculer effectivement la solution. Usuellement, ce calcul se fait dans la procédure C++ produite par MAPLE mais il sera possible de récupérer dans MAPLE les boîtes contenant les solutions et d'effectuer un calcul similaire en multi-précision pour calculer les solutions avec une précision arbitraire.
Prenons un exemple très simple d'utilisation de cette interface: on
désire trouver les solutions en ![]() des équations
des équations ![]() et
et ![]() pour
pour ![]() dans l'intervalle [-2,2]. Sous MAPLE cette
résolution se fera avec les instructions suivantes:
dans l'intervalle [-2,2]. Sous MAPLE cette
résolution se fera avec les instructions suivantes:
with(ALIAS): # 1 `ALIAS/use_3B`:=1: #2 HullConsistency([x^2+y^2-1,x+y],[x,y],"Simp",0.1): #3 SOL:=HessianSolve([x^2+y^2-1,x+y],[x,y],[[-2,2],[-2,2]],"Simp"); #4
- L'instruction 1 correspond au chargement de l'interface MAPLE d'ALIAS,
- dans l'instruction 2 on indique que pour la résolution on utilisera la méthode 3B,
- l'instruction 3 permet de produire dans le
fichier C++ "Simp.C" une procédure de nom "Simp" qui implante la
méthode 2B pour le système que l'on désire résoudre. En
l'occurrence, ce programme va vérifier que pour des intervalles
donnés en
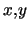 les valeurs des intervalle des paires suivantes sont
cohérentes entre elles: (
les valeurs des intervalle des paires suivantes sont
cohérentes entre elles: (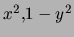 ),(
),(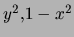 ),(
),( ,
(
,
( . Si elles ne le sont pas il corrigera la valeur des intervalles
pour
. Si elles ne le sont pas il corrigera la valeur des intervalles
pour 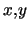 pour qu'elles le deviennent ou indiquera que cela n'est pas
possible et retournera une valeur indiquant l'absence de solution
dans la boîte proposée. Ainsi, si la borne supérieure de
l'intervalle
pour qu'elles le deviennent ou indiquera que cela n'est pas
possible et retournera une valeur indiquant l'absence de solution
dans la boîte proposée. Ainsi, si la borne supérieure de
l'intervalle 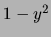 est strictement négative, il ne peut pas y avoir
cohérence
de la première paire puisque
est strictement négative, il ne peut pas y avoir
cohérence
de la première paire puisque 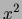 est toujours positif. Le dernier
paramètre de la procédure HullConsistency est une valeur
optionnelle qui indique que si lors du traitement des intervalles la
largeur d'un intervalle pour une variable varie de plus de 0.1, alors
après avoir traité l'ensemble des équations, on répétera le
filtrage en utilisant toute les équations qui contiennent cette
variable,
est toujours positif. Le dernier
paramètre de la procédure HullConsistency est une valeur
optionnelle qui indique que si lors du traitement des intervalles la
largeur d'un intervalle pour une variable varie de plus de 0.1, alors
après avoir traité l'ensemble des équations, on répétera le
filtrage en utilisant toute les équations qui contiennent cette
variable,
- la procédure HessianSolve de l'instruction 4 constitue
le c
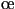 ur de l'algorithme de résolution. Cette procédure va
créer le code C++ nécessaire pour la résolution (en l'occurrence
des routines
d'évaluation des équations, de la jacobienne et de la hessienne du
système ainsi qu'un programme principal faisant appel à une
procédure de résolution qui admet comme argument optionnel une
procédure C++ de filtrage, ici la procédure Simp).
Après écriture du
code C++ la procédure HessianSolve lance la compilation puis
l'exécution du code, les résultats étant écrits dans un
fichier. Après cette exécution, la procédure lit les résultats
dans ce fichier et va les affecter à la variable MAPLE SOL.
ur de l'algorithme de résolution. Cette procédure va
créer le code C++ nécessaire pour la résolution (en l'occurrence
des routines
d'évaluation des équations, de la jacobienne et de la hessienne du
système ainsi qu'un programme principal faisant appel à une
procédure de résolution qui admet comme argument optionnel une
procédure C++ de filtrage, ici la procédure Simp).
Après écriture du
code C++ la procédure HessianSolve lance la compilation puis
l'exécution du code, les résultats étant écrits dans un
fichier. Après cette exécution, la procédure lit les résultats
dans ce fichier et va les affecter à la variable MAPLE SOL.
Une autre caractéristique intéressante de l'utilisation sous MAPLE est que chaque algorithme existe sous une forme parallèle permettant l'utilisation simultanée, via pvm, de plusieurs machines pour la résolution d'un problème donné. Ainsi dans l'exemple précédent on aurait pu utiliser la procédure ParallelHessianSolve en place de HessianSolve en indiquant simplement en plus dans les arguments une liste de nom de machines qui seraient utilisées pour le traitement.
ALIAS a été testée sur des systèmes très divers faisant intervenir jusqu'à 400 inconnues. La conception modulaire de ce logiciel a permis de mettre à la disposition du projet MIAOU un module qui est utilisé pour le calcul de filtre HF. Il est clair qu'ALIAS sera un des éléments constituant de la future plate-forme générique que nous comptons développer.
Interlog (consistance)
Interlog a été développé en collaboration avec Thales
"Systèmes
Aéroportés". Il s'agit d'un système de résolution de
contraintes sur les intervalles reposant sur la 2B-consistance et la
3B-consistance. Thales `Systèmes Aéroportés'' développe
actuellement
une version commerciale
d'Interlog.
CCC (coopération de solveurs)
CCC est un prototype de système coopératif concurrent
pour la
résolution de contraintes sur les
réels [32,31]. Il a
été développé en Oz et contient un solveur linéaire
utilisant
l'algorithme du simplexe, et un solveur non-linéaire. Il avait
pour
objectif de valider un modèle de coopération reposant sur une
communication fine entre des solveurs travaillant de
manière
concurrente sur un même ensemble de contraintes. Le point clef
est le
fait que la gestion des communications est effectuée par des
processus concurrents qui mettent à jour les contraintes
traitées
par les
différents solveurs. Ce modèle permet de remédier à la
principale
limite d'une architecture coopérative reposant sur un mode de
communication asynchrone entre les solveurs et qui réside dans
l'exploitation tardive des résultats obtenus par les différents
solveurs.
Les expérimentations menées avec CCC ont montré qu'une
telle
approche permettait d'obtenir à la fois des gains de performance
et
de précision significatifs.
Prospective logicielle
On peut distinguer deux types de logiciels qui seront développés dans le projet:- la plate-forme logicielle unique permettant à la fois le test des outils existants sur un problème donné ainsi que le développement de nouvelles méthodes dans le cadre d'un formalisme commun dont le développement s'étalera sur la durée de vie du projet. Cette plate-forme, servira de plus de vitrine pour le projet et constituera une des activités majeures du projet dès son démarrage.
- des logiciels dédiés à des applications spécifiques et qui auront été optimisés pour celles-ci. La base de ces logiciels pourra être développée à partir de la plate-forme qui sera, au fur et à mesure des tests, progressivement dépouillée des méthodes les moins efficaces et des codes inutiles pour atteindre les performances optimales.
Bibliographie
- 1
-
Beldiceanu N. et Contejean E.
Introducing global constraints in chip.
Journal of Mathematical and Computer Modelling, 20(12):97-123, 1994. - 2
-
Benhamou F., Mc Allester D., et Van Hentenryck P.
Clp(intervals) revisited.
In Proc. Logic Programming, 1994. - 3
-
Bliek C., Neveu B., et Trombettoni G.
Using graph decomposition for solving continuous csps.
In International Conference on Constraint Programming, CP'98, volume 1520 of LNCS, pages 102-116. Springer, 1998. - 4
-
Collavizza M., F. Delobel, et Rueher M.
Comparing partial consistencies.
Reliable Computing, 5:1-16, 1999. - 5
-
Collavizza M., F. Delobel, et Rueher M.
Extending consistent domains of numeric csp.
In IJCAI-99, pages 406-411, Stockholm, 1999. - 6
-
Dedieu J-P. et Yakoubsohn J-C.
Polynomial root finding: A statistical study of a bisection-exclusion algorithm.
Rapport de Recherche 95-04, LAO, Toulouse, 1995. - 7
-
Erdman A.G.
Modern Kinematics.
Wiley, New-York, 1993. - 8
-
Gotlieb A., Botella B., et Rueher M.
Automatic test data generation using constraint solving techniques.
In Symposium on Software Testing and Analysis, ISSTA'98, volume ACM SIGSOFT, vol. 2, pages 53-62, Clearwater Beach, USA, 1998. - 9
-
Gotlieb A., Botella B., et Rueher M.
A clp framework for computing structural test data.
In CL2000, First Int. Conf. on Computational Logic, volume 1861 of LNCS, pages 399-413. Springer, 2000. - 10
-
Granvilliers L. et Monfroy E.
Declarative modelling of constraint propagation strategies.
In Proc. ADVIS 2000, pages 201-215, 2000. - 11
-
Hansen E.
Global optimization using interval analysis.
Marcel Dekker, 1992. - 12
-
Harvey W.D. et Ginsberg M.L.
Limited discrepancy search.
In Proceedings of the International Joint Conference
on Artificial Intelligence, 1995.
International Joint Conference
on Artificial Intelligence, 1995.
- 13
-
Jaulin L. et Walter E.
Guaranteed nonlinear parameter estimation via interval computations.
In Int. Conf. on Numerical analysis with automatic result verification, 1993. - 14
-
Kearfott R.B. et Manuel N. III.
INTBIS, a portable interval Newton/Bisection package.
ACM Trans. on Mathematical Software, 16(2):152-157, 6JanvierFévrierMars AvrilMaiJuinJuilletAoûtSeptembreOctobre NovembreDécembreEté 1990. - 15
-
Krawczyk R.
Newton-algorithmen zur bestimmung von Nullstellen mit Fehlerschranken.
Computing, 4:187-201, 1969. - 16
-
Lhomme O.
Consistency techniques for numeric CSPs.
In IJCAI93, pages 232-238, Chambéry, Août 1993. - 17
-
Merlet J-P.
Parallel robots.
Kluwer, Dordrecht, 2000. - 18
-
Merlet J-P.
A parser for the interval evaluation of analytical functions and its applications to engineering problems.
J. Symbolic Computation, 31:475-486, 2001. - 19
-
Merlet J-P.
ALIAS: an interval analysis based library for solving and analyzing system of equations.
In SEA, Toulouse, 14-16 6JanvierFévrierMars AvrilMaiJuinJuilletAoûtSeptembreOctobre NovembreDécembreEté 2000. - 20
-
Merlet J-P.
Determination of 6d workspaces of Gough-type parallel manipulator and comparison between different geometries.
Int. J. of Robotics Research, 18(9):902-916, 10JanvierFévrierMars AvrilMaiJuinJuilletAoûtSeptembreOctobre NovembreDécembreEté 1999. - 21
-
Meseguer P.
Interleaved Depth-First Search.
In Proceedings of the International Joint
Conference on Artificial Intelligence, pages 1382-1387, 1997.
International Joint
Conference on Artificial Intelligence, pages 1382-1387, 1997.
- 22
-
Moore R.E.
Methods and Applications of Interval Analysis.
SIAM Studies in Applied Mathematics, 1979. - 23
-
Neumaier A.
Interval methods for systems of equations.
Cambridge University Press, Cambridge, 1990. - 24
-
Nuijten W.P.
Time and Resource Constrained Scheduling: A Constraint Satisfaction Approach.
Thèse de doctorat, Eindhoven University of Technology, 1994. - 25
-
Older W.J. et Velino A.
Extending prolog with constraint arithmetic on real intervals.
In IEEE Canadian conference on Electrical and Computer Engineering, 1990. - 26
-
Papegay Y., Merlet J-P., et Daney D.
Exact kinematics analysis of car's suspension mechanisms using symbolic computation and interval analysis.
ASME J. of Mechanical Design, 2001.
soumis. - 27
-
Prcovic N. et Neveu B.
Ensuring a Relevant Visiting Order of the Leaf Nodes during a Tree Search.
In Principles and Practice of Constraint Programming, CP'99, volume LNCS 1713, pages 361-374, 1999. - 28
-
Ratscheck H. et Rokne J.
Interval methods.
In Horst R. et Pardalos P.M., editors, Handbook of global optimization, pages 751-819. Kluwer, 1995. - 29
-
Régin J-C.
A filtering algorithm for constraints of difference in CSPs.
In Proc. of AAAI94, pages 362-367, Seattle, Washington, 1994. - 30
-
Régin J-C. et Rueher M.
A global constraint combining a sum constraint and difference constraints.
In International Conference on Constraint Programming, CP'2000, volume 1894 of LNCS, pages 384-395, Singapore, 2000. - 31
-
Rueher M. et Solnon C.
Concurrent cooperating solvers over the reals.
In INTERVAL'96, Wrzburg, Germany, 1996. - 32
-
Rueher M. et Solnon C.
Concurrent cooperating solvers over reals.
Reliable Computing, 3(3):325-333, 1997. - 33
-
Simonis H.
Problem classification scheme for finite domain constraint solving.
In CP96, Workshop on Constraint Programming Applications: An Inventory and Taxonomy, pages 1-26, Cambridge, MA, USA, 1996. - 34
-
Tapia R.A.
The Kantorovitch theorem for Newton's method.
American Mathematic Monthly, 78(1.ea):389-392, 1971. - 35
-
Trombettoni Gilles.
A polynomial time local propagation algorithm for general dataflow constraint problems.
In International Conference on Constraint Programming, CP'98, volume 1520 of LNCS, pages 432-446. Springer, 1998. - 36
-
Van Hentenryck P.
The OPL Optimization Programming Language.
MIT Press, Cambridge, 1999. - 37
-
Van Hentenryck P., Michel L., et Deville Y.
Numerica: a modeling language for global optimization.
MIT Press, Cambridge, 1997. - 38
-
Walter E. et Pronzato L.
Identification of parametric models from experimental data,.
Springer-Verlag, New-York, 1997. - 39
-
Yamamura K., Kawata H., et Tokue A.
Interval solution of nonlinear equations = using linear programming.
BIT, 38(1):186-199, 1998.
Index
- Alcatel
- ALM
- Amadeus
- applications ,
![[*]](crossref.png)
- ARENAIRE
- arithmetique@arithmétique par intervalles ,
![[*]](crossref.png)
- BIAS
- bibliographie
- biologie moléculaire ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- bissection ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- box-consistance
- calcul formel ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- CAO ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- CCC@CCC ,
![[*]](crossref.png)
- CEA
- certification ,
![[*]](crossref.png)
- CHIC-2
- CHIP@CHIP
- Claire@Claire
- CLP@CLP
- CMW
- CNES
- CNRS
- collaboration
- conception optimale
- consistance ,
![[*]](crossref.png)
- consistance,2B ,
![[*]](crossref.png)
- consistance,3B
- consistance,box
- CONTRAINTES
- contrats
- CPLEX@CPLEX
- CSP ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- Dassault
- Declic@Declic
- decomposition@décomposition ,
![[*]](crossref.png)
- Deltalab
- determinant@déterminant ,
![[*]](crossref.png)
- deuxbcon@2B-consistance ,
![[*]](crossref.png)
- dichotomie ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- distance,équations
- donnees@données
- ECLIPSE@Eclipse
- enseignement
- ERCIM
- erreurs numériques
- ESRF
- filtrage ,
![[*]](crossref.png)
- fonction d'évaluation
- fonction d'évaluation,naturelle
- fonction smear
- fonction,distances
- fonction,trigonométrique
- génération de jeux de test ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- GALAAD ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- geometrie@géométrie ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- gradient
- graphique ,
![[*]](crossref.png)
- ILOG
- inegalites@inégalités ,
![[*]](crossref.png)
- Inka
- interface ,
![[*]](crossref.png)
- intervalle
- Kantorovitch
- Krawczyk
- Lande ,
![[*]](crossref.png)
- Laue Langevin
- logiciel
- logiciel,ALIAS
- logiciel,génération des jeux de test
- logiciel,graphique
- logiciel,Inka
- logiciel,Interlog
- logiciel,mécanisme
- logiciel,plate-forme ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- MAPLE
- mathématiques expérimentales
- mecanisme@mécanisme ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- MIAOU ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- Micro Controle
- micro-robot
- MIPS ,
![[*]](crossref.png)
- monotonicité
- Moore
- MPFI ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- MPFR
- mpi@mpi
- Newton ,
![[*]](crossref.png)
- Newton par intervalles
- Numerica
- NUMOPT
- opérateur,de Krawczyk
- opl@OPL
- optimisation ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- ORION
- parallelisation@parallélisation ,
![[*]](crossref.png)
- parser
- plate-forme logicielle ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- PRISME
- Profil
- PROTHEO
- pvm@pvm
- QUAD-CLP@QUAD-CLP
- RISC-CLP@RISC-CLP
- ROBEA
- robot parallèle
- robustesse ,
![[*]](crossref.png) ,
, ![[*]](crossref.png) ,
, ![[*]](crossref.png)
- round-robin
- Scheduler@Scheduler
- simplexe
- Simulog
- smear
- solveur
- solveur,ALIAS
- solveur,collaboration entre ,
![[*]](crossref.png)
- solveur,Interlog
- solveur,spécifique ,
![[*]](crossref.png)
- SPACES ,
![[*]](crossref.png)
- test,de Kantorovitch
- test,de Moore
- tests logiciels
- Thales ,
![[*]](crossref.png)
- tolerance@tolérance ,
![[*]](crossref.png)
- Top Solid
- trigonometrie@trigonométrie ,
![[*]](crossref.png) ,
, ![[*]](crossref.png)
- troisbcon@3B-consistance
- type de solutions ,
![[*]](crossref.png)
- valorisation
- VisOpt
- Yamamura
- ALM
Table des matières
- Composition de l'équipe
- Introduction
- Programmation par contraintes
- Contraintes, Optimisation et Analyse par Intervalles
- Les limitations de la programmation par contraintes
- Complémentarité et apport des équipes
- Programme de recherche
- Méthodes de résolution
- Outils pour les méthodes de résolution
- Données, optimisation et type de solutions
- Domaines d'application
- Programme de travail à moyen terme
- Collaborations scientifiques
- État des lieux
- Positionnement par rapport aux projets INRIA
- Collaborations existantes
- Activités nationales
- Activités internationales
- Valorisation
- Contrats industriels actuels
- Autres contacts
- Prospective
- Enseignement
- Séminaires et Colloques
- Web
- Logiciels
- Annexe: Exemples de problèmes
- Un premier exemple: conception optimale de systèmes
- Un deuxième exemple: la génération automatique de jeux de tests logiciels
- Annexe: Consistances et Analyse par Intervalles
- Annexe: Limitations de la programmation par contraintes
- Annexe: Axe méthodes de résolution
- Consistance et analyse par intervalles: les méthodes hybrides
- Solveurs spécifiques
- Collaboration entre solveurs
- Annexe: Axe outils pour les méthodes de résolution
- Techniques de filtrage
- Choix des variables de bissection
- Techniques de décomposition
- Recherche arborescente
- Annexe: Axe données, optimisation et type de solutions
- Annexe: Domaines d'application
- Annexe: Positionnement par rapport aux projets INRIA
- Logiciels existants et en devenir
- Outil de visualisation graphique
- Outils de modélisation et d'analyse pour mécanisme
- Outil Inka de génération de jeux de test
- Solveurs
- Prospective logicielle
- Bibliographie
- Index
Notes
- ... 2B1
- COPRIN est par essence un projet transversal qui pourrait trouver aussi sa place dans le thème 4A
- ... H\'el\`ene2
- http://www.essi.fr/helen/mapage.html
- ...3
- http://www.inria.fr/coprin/equipe/merlet/merlet.html
- ... Bertrand4
- http://www-sop.inria.fr/cermics/contraintes/personnel/neveu/index.htm l
- ... Yves5
- http://www-sop.inria.fr/coprin/equipe/papegay/index.html
- ... Michel6
- http://www.essi.fr/~rueher
- ... structur\'ee7
- pour l'approche "contrainte" voir http://www.cs.unh.edu/ccc/archive/
- ...78
- pour l'analyse par intervalles voir http://www.cs.utep.edu/interval-comp
- ... mol\'eculaire9
- http://www.cs.unh.edu/ccc/archive/applications.html, http://www.cs.city.ac.uk/ drg/cp97-workshop/07:gilbert-eidhammer-jonassen.html
- ... g\'eom\'etriques10
- http://www.cs.purdue.edu/homes/cmh/electrobook/intro.html
- ... personnels11
- http://www.cosytec.fr/english/homepag2.htm
- ...1112
- http://www.ilog.fr/industries/transportation/flightops/
- ...BIAS/Profil13
- http://www.ti3.tu-harburg.de/Software/PROFILEnglisch.html
- ... arithmetic14
- http://www.sun.com/forte/cplusplus/interval/index.html
- ...InC++15
- http://www.cs.helsinki.fi/u/eahyvone/publications/iaai99_ps.zi p
- ...INTBLAS16
- http://happy.dt.uh.edu/ hu/INTBLAS/IBLAS.ps
- ...XSC17
- http://www.uni-karlsruhe.de/ iam/html/language/xsc-sprachen. html
- ...pvm 18
- http://www.netlib.org/pvm3/index.html
- ...mpi 19
- http://www.erc.msstate.edu/research/labs/hpcl/projects/mpi/index.html
- ... benchmarks20
- http://www.cs.unh.edu/ccc/archive/
- ... techniques21
- On rappelle que les bornes supérieures de complexité en temps des outils de satisfaction de contraintes sont peu pertinentes en pratique, d'où le concept de mathématiques expérimentales prôné dans le projet SPACES par exemple.
- ... contraintes22
- voir par exemple le logiciel SWORD http://www.bath.ac.uk/ensgm/con_mod.html
- ... Solver23
- http://www.ilog.fr
- ...CHIP24
- http://www.cosytec.fr
- ... IV25
- http://prologia.fr/
- ...Declic26
- http://www.sciences.univ-nantes.fr/info/perso/permanents/goualard/Research/software.html#DecLIC-target
- ... VML27
- http://www.insol.co.il
- ... Rouillier28
- http://calfor.lip6.fr/rouillie/Software/RS/
http://calfor.lip6.fr/jcf/Software/index.html - ... )29
- http://www-sop.inria.fr/coprin/logiciels/ALIAS/ALIAS.html