Gang XU
GALAAD Team, INRIA Sophia Antipolis
Sophia Antipolis, France
Isogeometric analysis and shape optimization
For a full verison of my work on isogeometric analysis, please visit the following isogeometry page on GALAAD-Wiki:
My current research interests on this topic include:
- IGA Toolbox;
- Parameterization of Computational domain in isogeometric analysis; Parameterization of computational domain plays important role in isogeometric analysisas mesh generation in finite element analysis. Two kinds of method are proposed to construct computational domain from given boundary CAD geometry: constraint optimization method and varational harmonic method.
- r-refinement in isogeometric analysis;
- IGA method based on triangular B-splines;
- IGA method based on quasi-B-splines in non-polynomial spaces;
- IGA method based on multi-degree B-splines.
- Optimal analysis-aware parameterization of computational domain in isogeometric analysis
Gang Xu, Bernard Mourrain, Régis Duvigneau, André Galligo
Proc. of Geometric Modeling and Processing (GMP 2010), 2010, 2010, 236-254 [ pdf ] - Parametrization of computational domain in isogeometric analysis: methods and comparison . In preparation.
- Isogeometric analysis using triangular B-splines. In preparation
- Isogeometric analysis using algebraic hyperbolic trigonometric B-splines. In preparation
- Isogeometric analysis using multi-degree B-splines. In preparation
- AHT B\'{e}zier curves and NUAHT B-spline curves
Gang Xu, Guozhao Wang
Journal of Computer Science and Technology, 2007, 22(4): 597-607 [ pdf ]
A plugin for 2D and 3D isogeometric analysis is developed in AXEL by GALAAD group and OPALE group at INRIA Sophia-Antipolis, which are involved in the European project EXCITING.
r-refinement in FEA is a remesh operation on computational domain to minimize the
cost function while keeping the number of elements as a constant. For isogeometric problems with unknown exact solutions, a residual-based posteriori error estimation for isogeometric analysis is proposed. The posteriori error estimation is obtained by inverse mapping from solution field to computational domain, which uses the basic idea of isogeometric analysis. Then from this error estimation, r-refinement can reposition the inner control points to minimize the error estimator. For r-refinement, the difference with h-refinement, p-refinement and k-refinement is that the number of control points and the degree of basis functions are unaltered and the positions of control points on the computational domain are subjected to change upon the required degree of accuracy. It can be considered as a parameterization method of computational domain in isogeometric analysis.
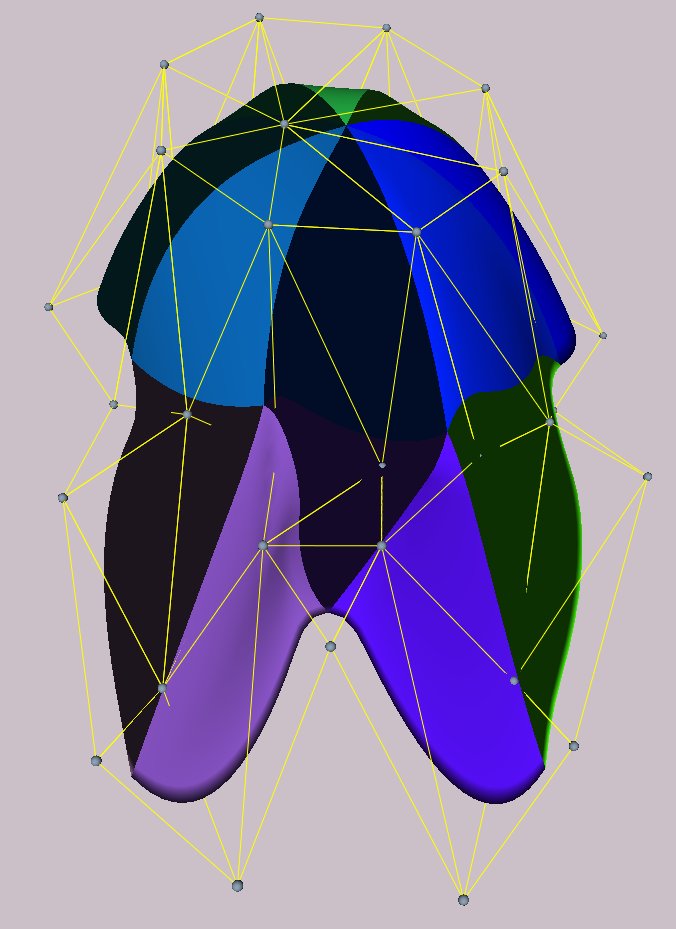
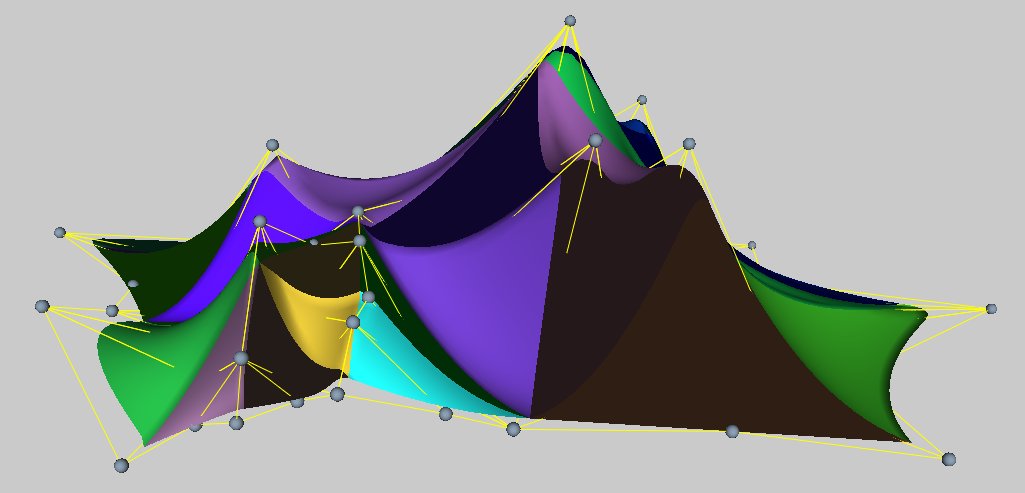
Here are some pictures of triangular B-splines, which has been implemented in AXEL as a plugin for editing and refinement. IGA with triangular B-splines is one of my ongoing work.


Publication
