|
CGAL 4.4 - High-dimension Triangulation
|
|
CGAL 4.4 - High-dimension Triangulation
|
This package proposes data structure and algorithms to compute triangulations of points in any dimensions. The Triangulation_data_structure allows to store and manipulate the combinatorial part of a triangulation while the geometric classes Triangulation and Delaunay_triangulation allows to compute a (Delaunay) triangulation of a set of points and to maintain it under insertions (and deletions in the Delaunay case).
A finite abstract simplicial complex is built on a finite set of vertices \( V\) and consists of a collection \( S\) of subsets of \( V\) such that
The sets in \( S\) (which are subsets of \( V\)) are called faces or simplices (the singular of which is simplex). A simplex \( s\in S\) is maximal if it is not a proper subset of some other set in \( S\).
A simplex having \( d+1 \) vertices is said of dimension \( d \). The simplicial complex is pure if all the maximal simplices have the same dimension.
If the vertices are embedded into Euclidean space \( \mathbb{R}^d\), we deal with finite simplicial complexes which have slightly different simplices and additional requirements:
See the wikipedia entry for more about simplicial complexes.
This CGAL package deals with pure manifold simplicial complexes which are connected and have no boundaries, which we will simply call in the sequel triangulations. It provides three main classes for creating and manipulating triangulations.
The class CGAL::Triangulation_data_structure<Dimensionality, TriangulationDSVertex, TriangulationDSFullCell> models an abstract triangulation: vertices in this class are not embedded in Euclidean space but are only of combinatorial nature.
CGAL::Triangulation<TriangulationTraits, TriangulationDataStructure> describes an embedded triangulation that has as vertices a given set of points and which fills the convex hull of these points. The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits, TriangulationDataStructure> adds further constraints to a triangulation, in that all its simplices must have the so-called Delaunay or empty-ball property: the interior of a ball circumscribing any simplex (or full cell) must be free from any vertex of the triangulation. The CGAL::Delaunay_triangulation class supports deletion of vertices.
An \( i\)-face denotes an \( i\)-dimensional simplex, or a simplex with \( i+1\) vertices. When these vertices are embedded in Euclidean space, they must be affinely independent.
If the maximal dimension of a simplex in the triangulation is \( d\), we call:
Two faces \( \sigma\) and \( \sigma'\) are incident if and only if \( \sigma'\) is a proper sub-face of \( \sigma\) or vice versa.
In this section, we describe the concept TriangulationDataStructure for which CGAL provides one model class: CGAL::Triangulation_data_structure<Dimensionality, TriangulationDSVertex, TriangulationDSFullCell>.
A TriangulationDataStructure can represent an abstract pure complex such that any facet is incident to exactly two full cells.
TriangulationDataStructure has a maximal dimension which is a TriangulationDataStructure and can then be queried using the method tds.maximal_dimension(). A TriangulationDataStructure also knows the current dimension of its full cells, which can be queried with tds.current_dimension(). In the sequel, let us denote the maximal dimension with \( D \) and the current dimension with \( d \). The inequalities \( -2 \leq d \leq D\) and \( 0 \le D\) always hold. The special meaning of negative values for \(d\) is explained below.
A TriangulationDataStructure can be viewed as a triangulation of the topological sphere \( \mathcal S^d\), i.e., its faces can be embedded to form a partition of \( \mathcal S^d\) into \(d\)-simplices.
One nice consequence of the above important fact is that a full cell has always exactly \( d+1\) neighbors. Two full cells \( \sigma\) and \( \sigma'\) sharing a facet are called neighbors.
TriangulationDataStructure. This corresponds to a single vertex.
This corresponds to two vertices, each corresponding to a full cell; the two full cells being neighbors of each other. This is the unique triangulation of the \( 0\)-sphere.
Triangulation_data_structureWe give here some details about the class Triangulation_data_structure<Dimensionality, TriangulationDSVertex, TriangulationDSFullCell> implementing the concept TriangulationDataStructure.
A TriangulationDataStructure explicitly stores its vertices and full cells.
Each vertex stores a reference (a handle) to one of its incident full cells.
Each full cell stores references to its \( d+1\) vertices and neighbors. Its vertices and neighbors are indexed from \( 0\) to \( d \). The indices of its neighbors have the following meaning: the \( i\)-th neighbor of \( \sigma\) is the unique neighbor of \( \sigma\) that does not contain the \( i\)-th vertex of \( \sigma\); in other words, it is the neighbor of \( \sigma\) opposite to the \( i\)-th vertex of \( \sigma\) (Figure Figure 40.1).
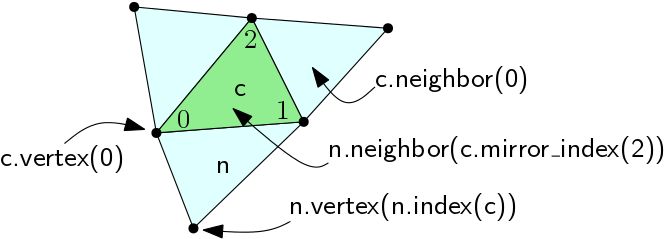
The Triangulation_data_structure<Dimensionality, TriangulationDSVertex, TriangulationDSFullCell> class template is designed in such a way that its user can choose
Dimensionality template parameter, TriangulationDSVertex template parameter and TriangulationDSFullCell template parameter. The last two parameters have default values and are thus not necessary, unless the user needs custom types (see the reference manual page for this class template). The first template parameter, Dimensionality, must be one of the following:
Dimension_tag<D> for some integer \( D \). This indicates that the triangulation can store full cells of dimension at most \( D \). The maximum dimension \( D \) is known by the compiler, which triggers some optimizations. Dynamic_dimension_tag. In this case, the maximum dimension of the full cells must be passed as an integer argument to an instance constructor (see TriangulationDataStructure). The TriangulationDSVertex and TriangulationDSFullCell parameters to the class template must be models of the concepts TriangulationDSVertex and TriangulationDSFullCell respectively. CGAL provides models for these concepts: Triangulation_ds_vertex<TriangulationDataStructure> and Triangulation_ds_full_cell<TriangulationDataStructure, TDSFullCellStoragePolicy>, which, as one can see, take the TriangulationDataStructure as a template parameter in order to get access to some nested types in TriangulationDataStructure.
CGAL::Triangulation_ds_vertex<TDS> and CGAL::Triangulation_ds_full_cell<TDS> where TDS is the current class Triangulation_data_structure<Dimensionality, TriangulationDSVertex, TriangulationDSFullCell> This creates a circular dependency, which we resolve in the same way as in the CGAL Triangulation_2 and Triangulation_3 packages (see Chapters chapterTDS2, chapterTriangulation2, chapterTDS3, and chapterTriangulation3). In particular, models of the concepts TriangulationDSVertex and TriangulationDSFullCell must provide a nested template Rebind_TDS which is documented in those two concept's reference manual pages. This mechanism can be used to provide a custom vertex or full cell class. The user is encouraged to read the documentation of the CGAL Triangulation_2 or Triangulation_3 package. The following examples shows how to construct a triangulation data structure by inserting vertices. Its main interest is that it demonstrates most of the API to insert new vertices into the triangulation.
File triangulation_data_structure_static.cpp
In the previous example, the maximal dimension is fixed at compile time. It is also possible to fix it at run time, as in the next example.
File triangulation_data_structure_dynamic.cpp
This example provides a function for computing the barycentric subdivision of a single full cell c in a triangulation data structure. The other full cells adjacent to c are automatically subdivided to match the subdivision of the full cell c. The barycentric subdivision of c is obtained by enumerating all the faces of c in order of decreasing dimension, from the dimension of c to dimension 1, and inserting a new vertex in each face. For the enumeration, we use a combination enumerator, which is not documented, but provided in CGAL.
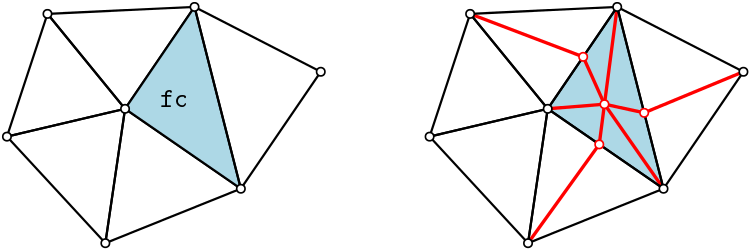
File barycentric_subdivision.cpp
CGAL::Triangulation<TriangulationTraits, TriangulationDataStructure> maintains a geometric triangulation in Euclidean space. More precisely, it maintains a triangulation (a partition into pairwise interior-disjoint full cells) of the convex hull of the points (the embedded vertices) of the triangulation. A special vertex at infinity is added to the convex hull facets to create infinite full cells and make the triangulation homeomorphic to a sphere of one dimension higher. Methods are provided for the insertion of points in the triangulation, the contraction of faces, the traversal of various elements of the triangulation as well as the localization of a query point inside the triangulation.
Infinite full cells outside the convex hull are each incident to a finite facet on the convex hull of the triangulation and to a unique vertex at infinity.
The class CGAL::Triangulation<TriangulationTraits, TriangulationDataStructure> stores a model of the concept TriangulationDataStructure which is instantiated with a vertex type that stores a point, and a full cell type that allows the retrieval of the point of its vertices.
The template parameter TriangulationTraits must be a model of the concept TriangulationTraits which provides the geometric Point type as well as various geometric predicates used by the Triangulation class.
TriangulationTraits must match the dimension of the TriangulationDataStructure. TriangulationDataStructure must be a model of the concept TriangulationDataStructure which provides the triangulation data structure as described in the previous section. The following example shows how to construct a triangulation in which we insert random points. In STEP 1, we generate one hundred random points in \( \mathcal R^5\), which we then insert into a triangulation. In STEP 2, we ask the triangulation to construct the set of edges ( \( 1\) dimensional faces) incident to the vertex at infinity. It is easy to see that these edges are in bijection with the vertices on the convex hull of the points. This gives us a handy way to count the convex hull vertices
triangulation1.cpp and triangulation2.cpp are given and commented below).
File triangulation.cpp
Remember that a triangulation triangulates the convex hull of its vertices. Each facet of the convex hull is incident to one finite full cell and one infinite full cell. In fact there is a bijection between the infinite full cells and the facets of the convex hull. If vertices are not in general position, convex hull faces that are not simplices are triangulated. So, in order to traverse the convex hull facets, there are (at least) two possibilities:
The first is to iterate over the full cells of the triangulation and check if they are infinite or not:
File triangulation1.cpp
A second possibility is to ask the triangulation to gather all the full cells incident to the infinite vertex: they form precisely the set of infinite full cells:
File triangulation2.cpp
infinite_full_cells. The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits, TriangulationDataStructure> derives from CGAL::Triangulation<DelaunayTriangulationTraits, TriangulationDataStructure> and adds further constraints to a triangulation, in that all its full cells must have the so-called Delaunay or empty-ball property: the interior of the ball circumscribing any full cell must be free from any vertex of the triangulation.
The circumscribing ball of a full cell is the ball having all vertices of the full cell on its boundary. In case of degeneracies (co-spherical points) the triangulation is not uniquely defined; Note however that the CGAL implementation computes a unique triangulation even in these cases.
When a new point p is inserted into a Delaunay triangulation, the finite full cells whose circumscribing sphere contain p are said to be in conflict with point p. The set of full cells that are in conflict with p form the conflict zone. That conflict zone is augmented with the infinite full cells whose finite facet does not lie anymore on the convex hull of the triangulation (with p added). The full cells in the conflict zone are removed, leaving a hole that contains p. That hole is ``star shaped'' around p and thus is easily re-triangulated using p as a center vertex.
Delaunay triangulations also support vertex removal.
The class CGAL::Delaunay_triangulation<DelaunayTriangulationTraits, TriangulationDataStructure> derives from CGAL::Triangulation<DelaunayTriangulationTraits, TriangulationDataStructure>. It thus stores a model of the concept TriangulationDataStructure which is instantiated with a vertex type that stores a geometric point and allows its retrieval.
The template parameter DelaunayTriangulationTraits must be a model of the concept DelaunayTriangulationTraits which provides the geometric Point type as well as various geometric predicates used by the Delaunay_triangulation class. The concept DelaunayTriangulationTraits refines the concept TriangulationTraits by requiring a few other geometric predicates, necessary for the computation of Delaunay triangulations.
When using a full cell type containing additional custom information, it may be useful to get an efficient access to the full cells that are going to be erased upon the insertion of a new point in the Delaunay triangulation, and to the newly created full cells. The second part of code example below shows how one can have efficient access to both the conflict zone and the created full cells, while still retaining an efficient update of the Delaunay triangulation.
File delaunay.cpp
The current implementation locates points by walking in the triangulation, and sorts the points with spatial sort to insert a set of points. Thus the theoretical complexity are \( O(n\log n)\) for inserting \( n\) random points and \( O(n^{\frac{1}{d}})\) for inserting one point in a triangulation of \( n\) random points. In the worst case, the expected complexity is \( O(n^{\lceil\frac{d}{2}\rceil}+n\log n)\).
The actual timing are the following:
This section will be completed, when the code will be fully ready (and preferably with the new Kernel).
This package is heavily inspired by the works of Monique Teillaud and Sylvain Pion (Triangulation_3) and Mariette Yvinec (Triangulation_2). The first version was written by Samuel Hornus and then pursued by Samuel Hornus and Olivier Devillers.