Symmetric tensors

using TensorDec

We consider symmetric tensors or equivalently homogeneous polynomials, in the following variables:

X = @ring x0 x1 x2;

A symmetric tensor of order d=4 and of rank 3.

d=4; F = (x0+x1+0.75x2)^d + 1.5*(x0-x1)^d -2.0*(x0-x2)^d

0.5x0^4 - 2.0x0^3x1 + 11.0x0^3x2 + 15.0x0^2x1^2 + 9.0x0^2x1x2 - 8.625x0^2x2^2 - 2.0x0x1^3 + 9.0x0x1^2x2 + 6.75x0x1x2^2 + 9.6875x0x2^3 + 2.5x1^4 + 3.0x1^3x2 + 3.375x1^2x2^2 + 1.6875x1x2^3 - 1.68359375x2^4

The graph of the homogeneous polynomial $(x_0+x_1+0.75x_2)^4 + 1.5(x_0-x_1)^4 -2(x_0-x_2)^4$ in polar coordinates on the sphere looks like this:

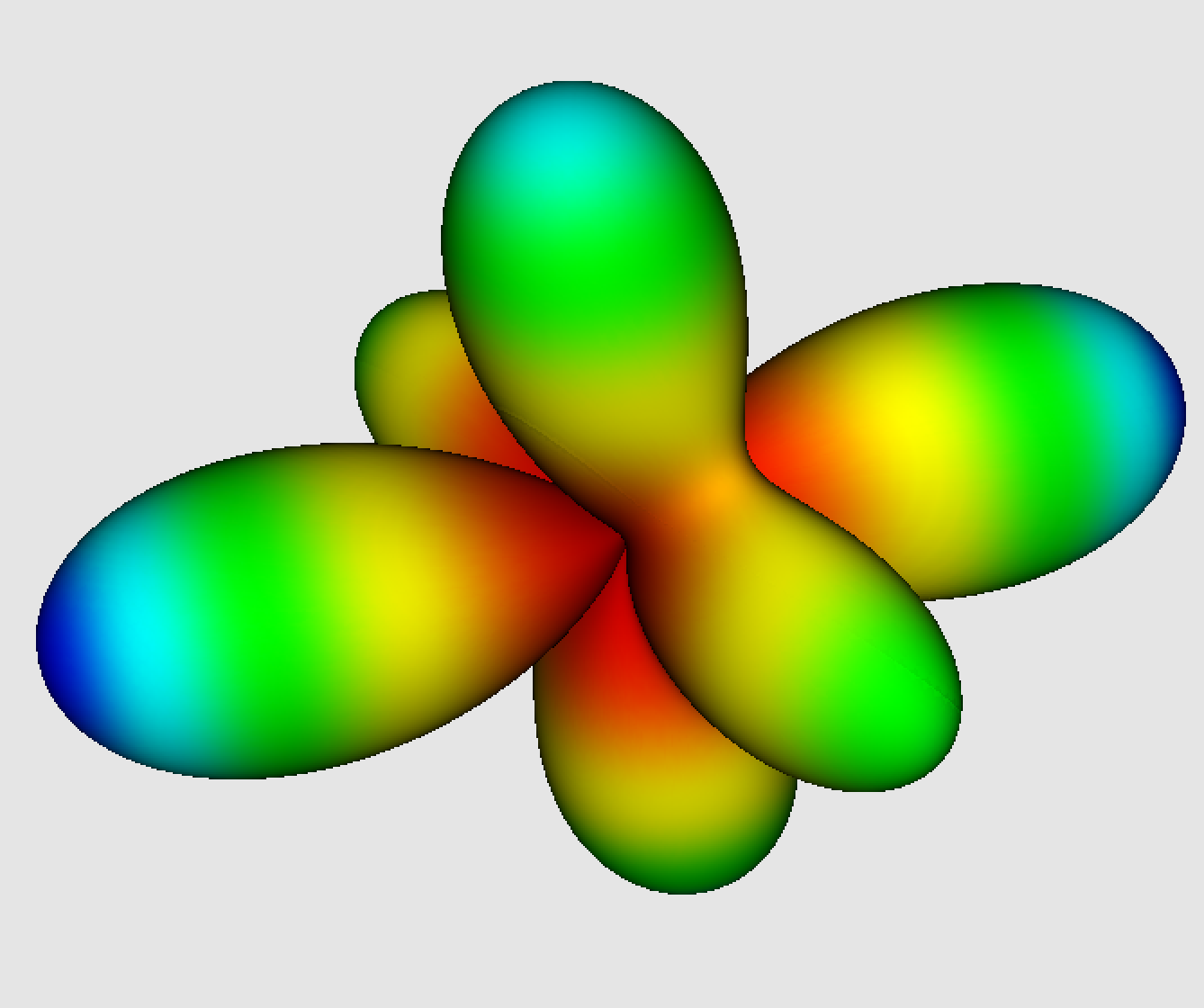
We associate to $t$, the following (truncated) series in the dual variables, after substituting $x_0$ by 1:

Computing its decomposition

w, Xi = decompose(F);

yields the weights w

w

3-element Array{Float64,1}:
 -2.0
  1.5
  1.0

and the corresponding points $\Xi$, which are the coefficient vectors of $x_0, x_1, x_2$ in the linear forms of the decomposition of the tensor F. They are normalized to have norm 1:

Xi

3×3 Array{Float64,2}:
  1.0           1.0          1.0 
 -2.71924e-16  -1.0          1.0 
 -1.0          -7.96799e-17  0.75