Definizioni

I1

 Definire una relazione le fra due numeri naturali che esprime che il primo numero è minore del secondo. 
Definition le: nat -> nat -> Prop :=
  fun a: nat =>
    fun b: nat =>
      fun c: nat => 
        exists c: nat, (eq b (plus a c))).

I2

 Definire una relazione lt fra due numeri naturali che esprime che il primo numero è strettamente minore del secondo. 
Definition lt: nat -> nat -> Prop :=
  fun a: nat =>
    fun b: nat =>
      (le a b) /\ ~(eq a b).

Costruzioni induttivi

J1

 Definire gli oggetti liste con il tipo list. 
Inductive list: Set -> Set :=
  nil : forall A: Set, (list A) 
| cons: forall A: Set, A -> (list A) -> (list A).
L'insieme A è un parametro comune a tutti i costruttori. Una variante di Inductive permette di rendere esplicito tale fatto: 
Inductive list (A: Set): Set :=
  nil : (list A) 
| cons: A -> (list A) -> (list A).
La lista [1] è rappresentata come: 
Check (cons nat (S O) (nil nat)).
(cons nat (S O) (nil nat))
     : (list nat)

J2

 Definire induttivamente la relazione le fra due numeri naturali che esprime che il primo numero è minore del secondo. 
Inductive le: nat -> nat -> Prop :=
  leN: forall n: nat, (le n n)
| leS: forall n: nat, forall m: nat, (le n m) -> (le n (S m)).

J3

 Definire induttivamente la relazione lt fra due numeri naturali che esprime che il primo numero è strettamente minore del secondo. 
Inductive lt: nat -> nat -> Prop :=
  ltN: forall n: nat, (lt n (S n))
| ltS: forall n: nat, forall m: nat, (lt n m) -> (lt n (S m)).

J4

 Definire induttivamente la proprietà Odd che esprime che un numero naturale è dispari. 
Inductive Odd: nat -> Prop :=
  Odd1 : (Odd (S O))
| OddSS: forall n: nat,  (Odd n) -> (Odd (S (S n))).

*J5

 Definire induttivamente un tipo btree che rappresenta gli alberi binari le cui foglie sono etichettate con numeri naturali. 
Inductive btree: Set :=
  Leaf: nat -> btree
| Node: btree -> btree -> btree.

*J6

 Definire un predicato induttivo checkB di tipo btree->Prop che corrisponde alla proprietà che un oggetto di tipo btree è stato costruito nel seguente modo:
ogni volta che è stato utilizzato il costruttore Node, il costruttore di testa del suo primo parametro è uguale al costruttore di testa del suo secondo parametro. 
Inductive checkB: btree -> Prop :=
  CheckLeaf : 
   forall n: nat,  (checkB (Leaf n))
| CheckNode0: 
   forall n1: nat, forall n2: nat, (checkB (Node (Leaf n1) (Leaf n2)))
| CheckNode1: 
   forall b1: btree, forall b2: btree, forall b3: btree, forall b4: btree,
    (checkB (Node b1 b2))->
      (checkB (Node b3 b4))->
      (checkB (Node (Node b1 b2) (Node b3 b4))).

*J7

 Definire induttivamente un tipo bin che rappresenta i numeri binari. 
Inductive bin: Set :=
   end: bin
| zero: bin -> bin
|  one: bin -> bin.

*J8

 Definire un predicato induttivo Full che esprime che un numero binario è composto solamente di 1 
Inductive Full: bin -> Prop :=
   FBa: (Full (one end))
|  FRi: forall b: bin, (Full b) -> (Full (one b)).

*J9

 Supponendo l'esistenza di un insieme di nodi node 
Parameter node: Set.
supponendo l'esistenza di un predicato Edge che mette in relazione due nodi. (Edge a b) significa che c'è una freccia da a verso b: 
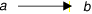
Parameter Edge: node -> node -> Prop.
definire 
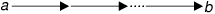
Definition Neighbour: node->node->Prop := 
  fun a: node => fun b: node => exists x: node, (Edge x a) /\ (Edge x b).

Inductive Connected: node->node->Prop :=
  Connected_Edge: 
   forall a: node, forall b: node, (Edge a b) -> (Connected a b)
| Connected_trans: 
   forall a: node, forall b: node, forall c: node,
      (Edge a b) -> (Connected b c) -> (Connected a c).

*J10

 Definire una relazione induttiva between fra tre numeri naturali che rappresenta il fatto che il secondo numero è compreso fra il primo e il terzo numero. 
Inductive between: nat -> nat -> nat -> Prop :=
   between_O: forall n: nat, (between n n n)
| between_S1: forall n: nat, forall m: nat, forall p: nat, (between n m p) -> (between n (S m) (S p))
| between_S2: forall n: nat, forall m: nat, forall p: nat, (between n m p) -> (between n m (S p))

J11

 Definire la funzione andb che calcola la congiunzione di due booleani. 
Definition andb: bool -> bool -> bool :=
  fun a: bool =>
    fun b: bool =>
      match a with
        true  => b
      | false => false
      end.

J12

 Definire la funzione orb che calcola la disgiunzione di due booleani. 
Definition orb: bool -> bool -> bool :=
  fun a: bool =>
    fun b: bool =>
      match a with
        true  => true
      | false => b
      end.

J13

 Usando l'esercizio J1, definire la funzione ricorsiva length che calcola la lunghezza di una lista. 
Fixpoint length (A: Set) (l: (list A)) {struct l}: nat := 
  match l with
     nil          =>  O
  | (cons _ _ l1) => (S (length A l1))
  end.

*J14

 Definire la funzione max che calcola il maggiore di due numeri naturali. 
Fixpoint max (a: nat) (b: nat) {struct a}: nat := 
  match a with
     O     => b
  | (S a1) => match b1 with
                 O     =>  a
              | (S b1) => (S (max a1 b1))
              end
  end.

*J15

 Definire la funzione ominus che prende due numeri naturali di tipo nat e restituisce un numero naturale che rappresenta la loro differenza simmetrica, ovvero il valore assoluto della loro differenza. (ominus 7 2) e (ominus 2 7) valgono 5. 
Fixpoint ominus (a: nat) (b: nat) {struct a}: nat :=
  match a with 
     O     => b
  | (S a1) => 
       match b with 
          O     =>  a
       | (S b1) => (ominus a1 b1)
       end
  end.

*J16

 Definire come funzione bmax che prende un oggetto a di tipo btree come definito nell'esercizio *J5 e restituisce il numero naturalle massimo che compare dentro a. 
Fixpoint bmax (a: btree) {struct a}: nat :=
    match a with
      (Leaf b) => b
    | (Node b c) => (max (bmax b) (bmax c))
    end.

*J17

 Definire come funzione byte che prende un numero binario a di tipo bin (come definito nell'esercizio *J7) e restituisce il suo numero di cifre. 
Fixpoint byte (a: bin) {struct a}: nat :=
  match a with 
     end      =>  O
  | (one a1)  => (S (byte a1))
  | (zero a1) => (S (byte a1))
 end.

*J18

 Definire come funzione bval che prende un numero binario a di tipo bin (come definito nell'esercizio *J7) e restituisce il suo valore. Si prende la convenzione che il binario 110 è rappresentato da destra a sinistra come (zero (one (one end))). 
Fixpoint bval (a: bin) {struct a}: nat :=
  match a with 
     end      =>  O
  | (one a1)  => (S (plus (bvar a1) (bvar a1)))
  | (zero a1) => (plus (bvar a1) (bvar a1))
 end.

*J19

 Definire come funzione ricorsiva la relazione le fra due numeri naturali che esprime che il primo numero è minore del secondo. 
Fixpoint le (n: nat) (m: nat) {struct n}: Prop := 
    match n with
       O     => True
    | (S n1) => 
         match m with
            O     =>  False
         | (S m1) => (le n1 m1)
         end
    end.

*J20

 Definire come funzione ricorsiva la relazione lt fra due numeri naturali che esprime che il primo numero è strettamente minore del secondo. 
Fixpoint lt (n: nat) (m: nat) {struct n}: Prop := 
    match n with
       O    => 
         match m with
            O     => False
         | (S m1) => True
         end
    | (S n1) => 
         match m with
            O     =>  False
         | (S m1) => (lt n1 m1)
         end
    end.

J21

 Definire come funzione ricorsiva la proprietà Odd che esprime che un numero naturale è dispari. 
Fixpoint Odd (n: nat) {struct n}: Prop :=
  match n with 
     O         =>  False
  | (S O)      =>  True
  | (S (S n1)) => (Odd n1)
  end.

J22

 Definire una funzione and_com di tipo forall A: Prop, forall B: Prop, (A /\ B) -> (B /\ A). 
Definition and_com: forall A: Prop, forall B: Prop, (A /\ B) -> (B /\ A) :=
  fun A: Prop =>
    fun B: Prop =>
      fun H: (A /\ B) =>
        match H with
          (conj H1 H2) => (conj B A H2 H1)
        end.

J23

 Definire una funzione or_com di tipo forall A: Prop, forall B: Prop, (A \/ B) -> (B \/ A). 
Definition or_com: forall A: Prop, forall B: Prop, (A \/ B) -> (B \/ A) :=
  fun A: Prop =>
    fun B: Prop =>
      fun H: (A \/ B) =>
        match H with
          (or_introl H1) => (or_intror B A H1)
        | (or_intror H1) => (or_introl B A H1)
        end.

*J24

 Definire una funzione double di tipo forall A: Prop, A -> (A /\ A). 
Definition double: forall A: Prop, A -> (A /\ A) :=
  fun A: Prop => fun H: A => (conj A A H).

*J25

 Definire una funzione mpc di tipo forall A: Prop, forall B: Prop, (A -> B) -> A -> (A /\ B). 
Definition mpc: forall A: Prop, forall B: Prop,   (A -> B) -> A -> (A /\ B) := 
  fun A: Prop => fun B: Prop => fun H: A -> B => fun H1: A => (conj A B H1 (H H1)).

*J26

 Definire una funzione cumul di tipo forall A: Prop, forall B: Prop, forall C: Prop, (A -> B) -> (A -> C)-> A -> (B /\ C). 
Definition cumul: forall A: Prop, forall B: Prop, forall C: Prop, (A -> B) -> (A -> C) ->  A -> (B /\ C) := 
  fun A: Prop => fun B: Prop => fun C: Prop => fun H: A -> B => fun H1: A->C =>  fun H2: A =>
    (conj B C (H H2) (H1 H2)).

*J27

 Definire una funzione triple di tipo forall A: Prop, forall B: Prop, forall C: Prop, A -> B -> C -> (A /\ (B /\ C)). 
Definition triple: forall A: Prop, forall B: Prop, forall C: Prop, A -> B -> C ->  (A /\ (B /\ C)) :=
  fun A: Prop => fun B: Prop => fun C: Prop => fun H1: A => fun H2: B => fun H3: C =>
    (conj A (B /\ C)  H1 (conj B C H2 H3)).

*J28

 Definire una funzione circ di tipo forall A: Prop, forall B: Prop, (A -> B) -> (B -> ~A) -> ~A. 
Definition circ: forall A: Prop, forall B: Prop, (A -> B) -> (B -> ~A) -> ~A :=
  fun A: Prop => fun B: Prop => fun H: A -> B => fun H1: B -> ~A =>
    fun H2: A => (H1 (H H2) H2).

*J29

 Definire una funzione nno di tipo forall A: Prop, forall B: Prop, (A -> ~B) -> B -> ~A . 
Definition no: forall A: Prop, forall B: Prop, (A -> ~B) -> B -> ~A :=
  fun A: Prop => fun B: Prop => fun H: A -> ~B => fun H1: B =>
    fun H2: A => (H H2 H1).

*J30

 Definire una funzione mpcQ di tipo forall A: Set, forall P: A -> Prop, (Q: A -> Prop) (R: A -> Prop) ((x: A) (P x) -> (Q x)) -> ((x: A) (P x) -> (R x)) -> ((x: A) (P x) -> ((Q x) /\ (R x))). 
Definition mpcQ: 
  forall A: Set, forall P: A -> Prop, forall Q: A -> Prop, forall R: A -> Prop,
    (forall x: A, (P x) -> (Q x)) -> 
      (forall x: A, (P x) -> (R x)) -> 
        (forall x: A, (P x) -> ((Q x) /\ (R x))) :=
  fun A: Set => fun P: A -> Prop => fun Q: A -> Prop => fun R: A -> Prop =>
    fun H: forall x: A, (P x) -> (Q x) =>
      fun H1: forall x: A, (P x) -> (R x) =>
        fun x: A => fun H2: (P x) =>
          (conj (Q x) (R x) (H x H2) (H1 x H2)).

*J31

 Definire una funzione cancel2 di tipo forall A: Set, forall P: A -> Prop, forall Q: A -> Prop, (R: A -> Prop) (forall x: A, (P x) -> (Q x) -> (R x)) -> (forall x: A, (Q x)) -> forall x: A, (P x) -> (R x)). 
Definition cancel2: 
  forall A: Set, forall P: A -> Prop, forall Q: A -> Prop, (R: A -> Prop) 
   (forall x: A, (P x) -> (Q x) -> (R x)) -> 
     (forall x: A, (Q x)) -> 
        forall x: A, (P x) -> (R x))
  fun A: Set => fun P: A -> Prop => fun Q: A -> Prop => fun R: A -> Prop =>
    fun H: forall x: A, (P x) -> (Q x) -> (R x) =>
      fun H1: forall x: A, (Q x) =>
        fun x: A => fun H2: (P x) =>
          (H x H2 (H1 x)).

*J32

 Definire una funzione instan di tipo forall A: Set, forall P: A -> Prop, (Q: A -> A -> Prop) (forall x: A, (P x) -> (y: A) (Q x y)) -> (forall x: A, (P x)) -> forall x: A, (Q x x). 
Definition instan: 
  (forall A: Set, forall P: A -> Prop, (Q: A -> A -> Prop) 
    (forall x: A, (P x) -> forall y: A, (Q x y)) -> 
      (forall x: A, (P x)) -> 
          forall x: A, (Q x x) :=
  fun A: Set => fun P: A -> Prop => fun Q: A -> A -> Prop => 
    fun H: forall x: A, (P x) -> forall y: A, (Q x y) =>
      fun H1: forall x: A, (P x) =>
        fun x: A => (H x (H1 x) x).

*J33

 Definire una funzione mp di tipo forall A: Set, forall a: A, forall P: A -> Prop, forall Q: A -> Prop, (forall x: A, (P x) -> (Q x)) -> (P a) -> (Q a). 
Definition mp: forall A: Set, forall a: A, forall P: A -> Prop,
forall Q: A -> Prop, (forall x: A, (P x) -> (Q x)) -> (P a) -> (Q a) :=
  fun A: Set => fun a: A => fun P: A -> Prop => fun Q: A -> Prop =>  fun H: forall x: A, (P x) -> (Q x) => fun H1: (P a) =>
    (H a H1).

J34

 Con la definitizione seguente 
Definition mconj: Prop -> Prop -> Prop := 
  fun A: Prop => fun B: Prop => forall P: Prop, (A -> B -> P) -> P.
Definire 
Definition mconj1: forall A: Prop, forall B: Prop, (mconj A B) -> A :=
  fun A: Prop => fun B: Prop => fun H: (mconj A B) =>
    (H A (fun H1: A => fun H2: B => H1)).

Definition mconj2: forall A: Prop, forall B: Prop, (mconj A B) -> B :=
  fun A: Prop => fun B: Prop => fun H: (mconj A B) => 
    (H B (fun H1: A => fun H2: B => H2)).

Definition mconj3: forall A: Prop, forall B: Prop, A -> B -> (mconj A B) :=
  fun A: Prop => fun B: Prop => fun H1: A => fun H2: B => (fun P: Prop => fun H3: A -> B -> P => 
    (H3 H1 H2)).

Definition mconj4: forall A: Prop, forall B: Prop, (mconj A B) -> (mconj B A) :=
  fun A: Prop => fun B: Prop => fun H: (mconj A B) =>
    (mconj3 B A (mconj2 A B H) (mconj1 A B H)).

*J35

 Con la definitizione seguente 
Definition mdisj: Prop -> Prop -> Prop :=
  fun A: Prop => fun B: Prop => forall P: Prop, (A -> P) -> (B -> P) -> P.
Definire 
Definition mdisj1: forall A: Prop, forall B: Prop, A -> (mdisj A B) :=
  fun A: Prop => fun B: Prop => fun H: A => fun P: Prop => fun H1: A -> P => fun H2: B -> P => 
      (H1 H).

Definition mdisj2: forall A: Prop, forall B: Prop, B -> (mdisj A B) :=
  fun A: Prop => fun B: Prop => fun H: B => fun P: Prop => fun H1: A -> P => fun H2: B -> P => 
      (H2 H).

Definition mdisj3: forall A: Prop, forall B: Prop, forall C: Prop, 
   (mdisj A B) -> (A -> C) -> (B -> C) -> C :=
  fun A: Prop => fun B: Prop => fun C: Prop => fun H: (mdisj A B) => fun H1: A -> C => fun H2: B -> C => 
      (H C H1 H2).
    

Definition mdisj4: forall A: Prop, forall B: Prop, (mdisj A B) -> (mdisj B A) :=
  fun A: Prop => fun B: Prop => fun H: (mdisj A B) =>
    (mdisj3 A B (mdisj B A) H (fun H1: A => (mdisj2 B A H1))
                              (fun H2: B => (mdisj1 B A H2))).

*J36

 Con le definitizioni seguenti 
Definition mfalse: Prop  := forall P: Prop, P.

Definition mneg: Prop -> Prop := fun A: Prop => A -> mfalse.
Definire 
Definition mfalse1: forall A: Prop, mfalse -> A :=
  fun A: Prop => fun H: mfalse => (H A).

Definition mfalse2: forall A: Prop, A -> (mneg A) -> mfalse :=
  fun A: Prop => fun H: A => fun H1: (mneg A) => (H1 H).

*J37

 Dare il principio d'induzione btree_ind che corrispondente al tipo btree definito all'esercizio *J5. 
   forall P: btree->Prop,
     (forall n: nat,  (P (Leaf n))) ->
     (forall b1: btree, forall b2: btree, (P b1) -> (P b2) -> (P (Node b1 b2))) ->
     (forall b: btree, (P b))

*J38

 Dare il principio d'induzione bin_ind che corrispondente al tipo bin definito all'esercizio *J7. 
  forall P: bin->Prop,
    (P end) ->
    (forall b: bin, (P b) -> (P (one b))) ->
    (forall b: bin, (P b) -> (P (zero b))) ->
       (forall b: bin, (P b))

*J39

 Dare il principio d'induzione between_ind che corrispondente alla relazione between definita all'esercizio *J10. 
 forall P: nat->nat->nat->Prop,
    (forall n: nat,  (P n n n)) ->
    (forall n: nat, forall m: nat, forall p: nat,
       (between n m p) -> (P n m p) -> (P n (S m) (S p))) ->
    (forall n: nat, forall m: nat, forall p: nat,
       (between n m p) -> (P n m p) -> (P n m (S p))) ->
    forall n: nat, forall m: nat, forall p: nat, (between n m p) -> (P n m p)

J40

 Scrivere in Coq l'algoritmo d'ordinamento per inserimento isort. 
(* inserimento di un elemento a dentro una lista ordinata L *)
Fixpoint insert (a: A) (L: list) {struct L}: list :=
 match L with
    nil        => (cons a nil)
 | (cons b L1) =>
      match (f_le a b) with  
        true  => (cons a L)
      | false => (cons b (insert a L1)) end
 end.

Fixpoint isort (L: list) {struct L}: list :=
 match L with 
    nil        =>  nil 
 | (cons a L1) => (insert a (isort L1)) end.

J42

 Scrivere in Coq il predicato Ordered_list che esprime che una lista di A è ordinata rispetto al predicato le. 
Inductive Ordered_list: list ->  Prop :=
   Ordered_nil   : (Ordered_list nil)
 | Ordered_single: forall a: A,  (Ordered_list (cons a nil))
 | Ordered_top   : forall a: A, forall b: A, forall L: list,
   (le a b) -> 
      (Ordered_list (cons b L)) ->  (Ordered_list (cons a (cons b L))) .

J43

Scrivere in Coq il predicato Permutation che esprime che una lista contiene gli stessi elementi con la stessa molteplicità di un'altra: per esempio, [1;1;2] ha gli stessi elementi di [1;2;1] ma ha un 1 in piú di [1;2]. 
(* ogni permutazione e' una sequenza di trasposizioni *)
Inductive Permutation: list -> list ->  Prop :=
   Is_perm_nil  : (Permutation nil nil)
 | Is_perm_skip : 
     forall a: A,
     forall L1: list, forall L2: list,
     (Permutation L2 L1) ->  (Permutation (cons a L2) (cons a L1))
 | Is_perm_swap : 
     forall a: A, forall b: A,
     (L: list)  (Permutation (cons a (cons b L)) (cons b (cons a L)))
 | Is_perm_trans: 
     forall L1: list, forall L2: list, forall L3: list,
     (Permutation L1 L2) -> (Permutation L2 L3) ->  (Permutation L1 L3).

J41

Scrivere in Coq il teorema che esprime che l'algoritmo isort è corretto. 
Theorem isort_correct: forall L: list, (Ordered_list (isort L)) /\ (Permutation L (isort L)).

Prove interattive

K1

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem trivial: forall A: Prop, A -> A.
intro A.
intro H.
exact H.
Qed.

K2

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem or_commutative: forall A: Prop, forall B: Prop, A \/ B -> B \/ A.
intro A.
intro B.
intro H.
case H.
intro H1.
right.
exact H1.
intro H1.
left.
exact H1.
Qed.

K3

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem mp: forall A: Prop, forall B: Prop, A -> (A -> B) -> B.
intro A.
intro B.
intro H.
intro H1.
apply H1.
exact H.
Qed.

K4

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem S: forall A: Prop, forall B: Prop, forall C: Prop, (A -> B -> C) -> (A -> B) -> A -> C.
intro A.
intro B.
intro C.
intro H'.
intro H'0.
intro H'1.
apply H'.
exact H'1.
apply H'0.
exact H'1.
Qed.

K5

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem Praeclarum: forall x: Prop, forall y: Prop, forall z: Prop, forall t: Prop, (x -> z) /\ (y -> t) -> x /\ y -> z /\ t.
intro x.
intro y. 
intro z.
intro t.
intro h.
case h.
intro h1.
intro h2.
intro h0.
case h0.
intro h3.
intro h4.
split.
apply h1.
exact h3.
apply h2.
exact h4.
Qed.

K6

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem resol: 
  forall p: Type -> Prop, forall q: Type -> Prop, forall a: Type,  (p a) -> (forall x: Type, (p x) -> (q x)) -> (q a).
intro p.
intro q.
intro a.
intro h.
intro h1.
apply h1.
exact h.
Qed.

K7

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem S: 
  forall A: Set,
  forall R: A -> A -> Prop, 
  (forall x: A, forall y: A, forall z: A, (R x y) /\ (R y z) -> (R x z)) -> (forall x: A, forall y: A, (R x y) -> (R y x)) -> 
  forall x: A, (exists y: A, (R x y)) -> (R x x).
intro A.
intro R.
intro Rtrans.
intro Rsym.
intro x.
intro h2.
case h2.
intro y.
intro R0.
apply (Rtrans x y).
split.
exact R0.
apply Rsym.
exact R0.
Qed.

K8

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem not_not: forall a: Prop, a -> ~ (~ a).
intro a.
intro h.
red.
intro h1.
case h1.
exact h.
Qed.

K9

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem mini_cases: forall x: Prop, forall y: Prop, (x \/ ~ y) /\ y -> x.
intro x.
intro y.
intro h.
case h.
intro h1.
intro h2.
case h1.
intro h3.
exact h3.
intro h3.
case h3.
exact h2.
Qed.

K10

 Dare la sequenza di tattiche che corrisponde alla prova di: 
Theorem not_quite_classic: forall a: Prop, ~ (~ (a \/ ~ a)).
intro a.
red.
intro h.
case h.
right.
red.
intro h1.
case h.
left.
exact h1.
Qed.
Laurent Théry