


suivant: Filtrage d'une instance complète
monter: Fermeture d'une instance
précédent: Fermeture d'une instance
Table des matières
Dans le problème de satisfaction de contraintes de distance, il y a
deux types données : d'une part les coordonnées des points, pour
lesquels on veut obtenir un filtrage optimal des domaines et d'autre part les
distances. Ces dernières ne garantissent pas toujours l'existence de solutions,
il faut que pour tout triplet de points les inégalités triangulaires soient vérifiées.
Grace à ces contraintes supplémentaires on peut borner les distances inconnues en utilisant
les distances données et le système d'inégalités, ce qui revient à compléter le graphe de distance.
Figure:
Fermeture du graphe de distance associé à l'exemple 1.1
|
|
La valuation des arètes du graphe
complet peut être calculée en résolvant le
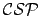 , qu'on notera INEQ(
, qu'on notera INEQ(
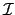 ), dont les
inconnues sont les distances entre les points, les domaines sont ceux de ces distances, et
les contraintes sont exprimées par l'ensemble de toutes les
inégalités triangulaires du système :
Étant donnée une instance quelconque
), dont les
inconnues sont les distances entre les points, les domaines sont ceux de ces distances, et
les contraintes sont exprimées par l'ensemble de toutes les
inégalités triangulaires du système :
Étant donnée une instance quelconque
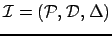 , on peut donc toujours
construire l' instance complète de
, on peut donc toujours
construire l' instance complète de
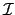 en calculant la fermeture du graphe de
distance qui lui est associé.
en calculant la fermeture du graphe de
distance qui lui est associé.
Pour chaque arête d'un triangle donné on a 2 contraintes, ce qui fait 6 contraintes par triangle.
Pour 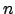 points donnés, on dénombre
points donnés, on dénombre
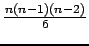 triangles, y compris les triangles dégénérés
si certains points sont confondus. Donc :
triangles, y compris les triangles dégénérés
si certains points sont confondus. Donc :
- le nombre de contraintes est
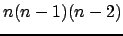
- le nombre de variables est
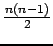
Puisque ce sont des contraintes linéaires, on peut utiliser l'algorithme du simplexe,
pour résoudre INEQ(
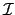 ).
).
La fermeture du graphe de distance nous garantit donc que tous les triangles du système sont
constructibles, quelles que soient les valeurs choisies dans les domaines des distances
entre ses sommets. Autrement dit on a une consistance de chemin réduite aux bornes des domaines
des distances sur INEQ(
 ). Or, cela n'implique pas qu'un polygône ayant plus de 3 côtés
soit constructible. Par exemple, le quadrilatère
). Or, cela n'implique pas qu'un polygône ayant plus de 3 côtés
soit constructible. Par exemple, le quadrilatère 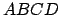 n'est pas constructible si on choisit
n'est pas constructible si on choisit 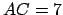 et
et 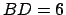 . En effet cela implique que
. En effet cela implique que  ,
,  et
et 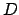 sont alignés car
sont alignés car 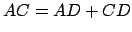 , et d'autre part
que
, et d'autre part
que 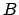 ,
, 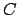 et
et 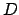 sont alignés car
sont alignés car 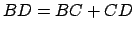 . Donc
. Donc 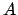 ,
, 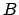 ,
, 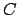 et
et 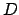 sont alignés, pourtant
aucune longueur n'est égale à la somme des 2 autres dans le triangle
sont alignés, pourtant
aucune longueur n'est égale à la somme des 2 autres dans le triangle 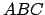 , ce qui est incohérent.
, ce qui est incohérent.

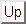


suivant: Filtrage d'une instance complète
monter: Fermeture d'une instance
précédent: Fermeture d'une instance
Table des matières
Heikel Batnini
2002-10-22
![\includegraphics[scale=0.8]{complete_quad.eps}](img194.png)
![$\displaystyle \forall i,j,k \in [1..n]: i \neq j \neq k \left\{
\begin{tabular}...
...$\delta_{i,j} \geq \vert\delta_{i,k} - \delta_{j,k}\vert$}
\end{tabular}\right.$](img196.png)
![]() ). Or, cela n'implique pas qu'un polygône ayant plus de 3 côtés
soit constructible. Par exemple, le quadrilatère
). Or, cela n'implique pas qu'un polygône ayant plus de 3 côtés
soit constructible. Par exemple, le quadrilatère ![]() n'est pas constructible si on choisit
n'est pas constructible si on choisit ![]() et
et ![]() . En effet cela implique que
. En effet cela implique que ![]() ,
, ![]() et
et ![]() sont alignés car
sont alignés car ![]() , et d'autre part
que
, et d'autre part
que ![]() ,
, ![]() et
et ![]() sont alignés car
sont alignés car ![]() . Donc
. Donc ![]() ,
, ![]() ,
, ![]() et
et ![]() sont alignés, pourtant
aucune longueur n'est égale à la somme des 2 autres dans le triangle
sont alignés, pourtant
aucune longueur n'est égale à la somme des 2 autres dans le triangle ![]() , ce qui est incohérent.
, ce qui est incohérent.