MATRIX Namespace Reference

Detailed Description

Module for generic implementations on dense matrices. The following signatures or definitions must at least be available for the type R : 
      typedef typename size_type;    //type of the indices.
      typedef typename value_type;   //type of the coefficients.

      size_type  R::nbrow();
      size_type  R::nbcol();
      value_type R::operator()(size_type i, size_type j);


Typedefs

typedef unsigned size_t

Functions

template<class R>
std::ostream & print (std::ostream &os, const R &m)
template<class M>
std::istream & read (std::istream &is, M &m, ByRow br=ByRow())
template<class M>
std::istream & read (std::istream &is, M &m, ByCol)
template<class R, class C>
void init (R &a, const C &c)
 Initialise all the entries of a with the value c.
template<class M>
void init (M &m, const typename M::value_type *data, ByRow)
template<class M>
void init (M &m, const typename M::value_type *data, ByCol)
template<class M>
void init (M &m, std::istream &ins, ByRow)
template<class M>
void init (M &m, std::istream &ins, ByCol)
template<class M, class Data, class Order>
void init (M &m, typename M::size_type nrw, typename M::size_type ncl, Data &data, Order)
template<class R, class Int>
void reserve (R &a, const Int &m, const Int &n)
 Reserve the memory space.
template<class M, class C>
void mul_ext (M &m, const C &c)
template<class V, class M>
void getrow (V &v, const M &m, int i)
template<class V, class M>
void getcol (V &v, const M &m, int i)
template<class SM, class M>
void submatrix (SM &sm, const M &m, const Range2d &rg)
template<class M, class Ma, class C>
void mul_ext (M &m, const Ma &a, const C &c)
template<class M, class C>
void div_ext (M &m, const C &c)
template<class M, class Ma, class C>
void div_ext (M &m, const Ma &a, const C &c)
template<class M>
void swaprow (M &m, int i, int j)
template<class M>
void swapcol (M &m, int i, int j)
template<class M, class C>
void addrow (M &m, typename M::size_type i, typename M::size_type j, const C &c)
template<class M, class C>
void addcol (M &m, int i, int j, const C &c)
template<class M, class C>
void multrow (M &m, int i, const C &c)
template<class M, class C>
void multcol (M &m, int i, const C &c)
template<class R1, class R2>
void assign (R1 &r, const R2 &m)
template<class R>
R::value_type trace (const R &M)
 Trace of a matrix.
template<class R, class S>
void add (R &a, const S &b)
 Inplace addition of matrices.
template<class R, class S, class T>
void add (R &a, const S &b, const T &c)
template<class R, class S>
void sub (R &a, const S &b)
template<class R>
void sub (R &a, const R &b, const R &c)
template<class R, class S, class T>
void mul (R &a, const S &b, const T &c)
template<class R, class S>
void mul (R &a, const S &b)
 Inplace multiplication of matrices.
template<class V, class M, class W>
void mul_vect (V &a, const M &b, const W &v)
template<class R>
void transpose (R &M)
 Inplace transposition.
template<class R>
bool equal (const R &a, const R &b)
template<class R>
void setupper (R &A)
template<class R>
void setlower (R &A)
template<class Vect, class Mat>
void svd (Vect &S, const Mat &A, Mat &Us, Mat &V)
template<class Vect, class Mat>
void svd (Vect &S, const Mat &A)
template<class R>
bool good_pivot (Bareiss, R &A)
template<class C, class O, class R>
bool good_pivot (Bareiss, MPol< C, O, R > &A)
template<class R>
R::value_type decomp (LU lu, R &A)
template<class R>
R::value_type decomp (Bareiss, R &A, unsigned &r)
template<class R>
R::value_type decomp (const Bareiss &mth, R &A)
template<class R>
R::size_type rank (const R &M)
template<class R>
R::size_type rank (const Bareiss &mth, const R &M)
template<class MAT>
void kronecker (MAT &r, const MAT &a, const MAT &b)

Function Documentation

template<class R, class S, class T>
void MATRIX::add ( R &  a,
const S &  b,
const T &  c 
)

Addition of matrices of the same size. The required space should be allocated for a.

Definition at line 266 of file MATRIX.m.

template<class R, class S>
void MATRIX::add ( R &  a,
const S &  b 
)

Inplace addition of matrices.

Definition at line 254 of file MATRIX.m.

template<class R1, class R2>
void MATRIX::assign ( R1 &  r,
const R2 &  m 
)

Assignement of a dense matrix to another one, assuming they have the same size, but not necessarily the same type.

Definition at line 234 of file MATRIX.m.

References assign().

Referenced by TopSbdBdg2d< O, X, I >::assign(), bezier::sbd2d< X, I, bezier::bzislv< X > >::assign(), and let::assign().

template<class R>
R::value_type MATRIX::decomp ( Bareiss  ,
R &  A,
unsigned &  r 
)

Bareiss method. The operations are performed inplace. The output value is the last element on the diagonal. If the matrix is invertible, it is its determinant. The rank is stored in rk.

Definition at line 620 of file MATRIX.m.

template<class R>
R::value_type MATRIX::decomp ( LU  lu,
R &  A 
)

Inplace LU decomposition of A.

Definition at line 571 of file MATRIX.m.

Referenced by decomp(), Decomp(), rank(), and Triang().

template<class C, class O, class R>
bool MATRIX::good_pivot ( Bareiss  ,
MPol< C, O, R > &  A 
)

Test if A is a good pivot when A is a multivariate polynomial.

Definition at line 558 of file MATRIX.m.

References MPol< C, O, R >::begin(), and MPol< C, O, R >::end().

template<class R>
bool MATRIX::good_pivot ( Bareiss  ,
R &  A 
)

Test if A is a good pivot.

Definition at line 549 of file MATRIX.m.

template<class R, class C>
void MATRIX::init ( R &  a,
const C &  c 
)

Initialise all the entries of a with the value c.

Definition at line 94 of file MATRIX.m.

Referenced by MatrDse< Seq< OCTREE::NODE_TYPE > >::MatrDse().

template<class MAT>
void MATRIX::kronecker ( MAT &  r,
const MAT &  a,
const MAT &  b 
)

Compute the Kronecker product of two matrices.

Definition at line 702 of file MATRIX.m.

template<class R, class S>
void MATRIX::mul ( R &  a,
const S &  b 
)

Inplace multiplication of matrices.

Definition at line 319 of file MATRIX.m.

References sturmseq::init().

template<class R, class S, class T>
void MATRIX::mul ( R &  a,
const S &  b,
const T &  c 
)

Multiplication of matrices. The required place should be allocated in a.

Definition at line 304 of file MATRIX.m.

template<class V, class M, class W>
void MATRIX::mul_vect ( V &  a,
const M &  b,
const W &  v 
)

Multiplication by a vector. The vector a should be first initialised with the correct size and zero entries.

Definition at line 346 of file MATRIX.m.

template<class R>
std::ostream& MATRIX::print ( std::ostream &  os,
const R &  m 
)

Output function for general matrices. It is called by the output operator << of the classes of matrices.

Definition at line 51 of file MATRIX.m.

template<class R>
R::size_type MATRIX::rank ( const Bareiss &  mth,
const R &  M 
)

Compute the rank of the matrix M, by applying a Bareiss decomposition. The index of the last non-zero row in this triangular matrix is the rank.

Definition at line 689 of file MATRIX.m.

References decomp().

template<class R>
R::size_type MATRIX::rank ( const R &  M  ) 

Rank, based on SVD computations. A numerical rank is determined by computing the first index where the ratio of the corresponding singular value by the largest one is smaller than the tolerance TOL.

Definition at line 674 of file MATRIX.m.

References linalg::rep1d< C >::size(), and svd().

Referenced by Rank().

template<class M>
std::istream& MATRIX::read ( std::istream &  is,
M &  m,
ByRow  br = ByRow() 
)

Input function for general matrices. The input format is of the form m n c00 c0 ... where m is the number of rows, n is the number of columns and the coefficients are read row by row.

Definition at line 68 of file MATRIX.m.

template<class R, class Int>
void MATRIX::reserve ( R &  a,
const Int &  m,
const Int &  n 
)

Reserve the memory space.

Definition at line 152 of file MATRIX.m.

template<class R>
void MATRIX::setlower ( R &  A  ) 

Assign the upper coefficients to 0 in order to get a lower triangular matrix.

Definition at line 409 of file MATRIX.m.

template<class R>
void MATRIX::setupper ( R &  A  ) 

Assign the lower coefficients to 0 in order to get an upper triangular matrix.

Definition at line 399 of file MATRIX.m.

template<class R>
void MATRIX::sub ( R &  a,
const R &  b,
const R &  c 
)

Substraction of matrices of the same size. The required space should be allocated for a.

Definition at line 290 of file MATRIX.m.

template<class R, class S>
void MATRIX::sub ( R &  a,
const S &  b 
)

Inplace substraction of matrices of the same size. The required space should be allocated for a.

Definition at line 279 of file MATRIX.m.

template<class Vect, class Mat>
void MATRIX::svd ( Vect &  S,
const Mat &  A 
)

Compute the singular values of the matrix A and put them in the vector S.

Definition at line 540 of file MATRIX.m.

References svd().

template<class Vect, class Mat>
void MATRIX::svd ( Vect &  S,
const Mat &  A,
Mat &  Us,
Mat &  V 
)

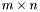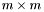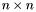Singular value decomposition of the matrix A. The singular values are output in S. In output, the matrix Us is the product of an orthogonal matrix by the diagnonal matrix of singular values, V is an orthogonal matrix and we have A=Us*Transpose(V). The matrix A is not modified but copied first in Us. If A is an $m\times n$ matrix, Us is $m\times m$ and V is $n \times n$.

The necessary memory space {must be allocated} in S and V, before calling this function: S should be of size max(A.nbrow(),A.nbcol()) and V of size (A.nbcol(),A.nbcol()). The matrix Us need not be preallocated, for it is assigned to a copy of A (Us=A).

It requires the functions or operators Norm, sqrt, +,-,*,/, <= for the coefficient field.

Definition at line 439 of file MATRIX.m.

Referenced by rank(), and svd().

template<class R>
R::value_type MATRIX::trace ( const R &  M  ) 

Trace of a matrix.

Definition at line 245 of file MATRIX.m.

template<class R>
void MATRIX::transpose ( R &  M  ) 

Inplace transposition.

Definition at line 362 of file MATRIX.m.

Referenced by MatrDse< Seq< OCTREE::NODE_TYPE > >::transpose().


SYNAPS DOCUMENTATION
logo