|
realroot_doc 0.1.1
|
|
realroot_doc 0.1.1
|
The class used to call the sleeve solver is
template<class C, class M> struct solver<ring<C,Monomials> >, ContFrac<M> >;
| C | is the coefficient type used for the subdivision, |
| M | in {Approximate, Isolate} specifies if the solver is isolating the roots or approximating them within a given precision |
It provides the functions of specified in the solver interface.
The roots are isolated in intervals.
Here is an example:
Seq<Interval<rational> > sol; polynomial< integer, with<MonomialTensor> > f = ...; solver< double, ContFrac<Isolate> >::solve(sol,f);
In the case, one want to isolate the roots on a given interval [a,b]=[-1,1], one can use the following instruction:
solver< double, ContFrac<Isolate> >::solve(sol,f,-1,1);
The roots are isolated in intervals of size bounded by the precision parameter of the solver. Here is an example:
Seq< Interval<rational> > sol; polynomial< integer, with<MonomialTensor> > f = ...; solver< double, ContFrac<Approximate> >::solve(sol,f);
In this example, we approximate the roots within the precision 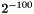 . The precision can be set globally:
. The precision can be set globally:
solver< double, ContFrac<Monomial,Approximate> >::set_precision(100);
In the case, one want to compute the roots on a given interval [a,b] (eg. [-1,1]), one can use the following instruction:
solver< double, ContFrac<Approximate> >::solve(sol,f,-1,1); solver< double, ContFrac<Approximate> >::solve(sol,f,prec,-1,1);