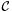 ,
,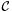 be a planar implicit curve defined by a polynomial equation
be a planar implicit curve defined by a polynomial equation 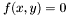 , where
, where ![$f \in \mathbbm{Q}[x, y]$](form_468.png) . We are going to describe an algorithm, which outputs a graph of points in the plane, \ isotopic to the curve
. We are going to describe an algorithm, which outputs a graph of points in the plane, \ isotopic to the curve 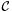 , and with the following properties:
, and with the following properties:
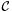 ,
,
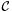 .
.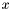 -axis. Then the topology of
-axis. Then the topology of 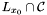 (where
(where 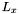 is the line orthogonal to the
is the line orthogonal to the 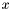 -axis through the point
-axis through the point 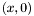 ) changes, when
) changes, when 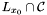 contains multiple points, that is when
contains multiple points, that is when
![\[ f (x, y) = 0, \partial_y f (x, y) = 0 \]](form_489.png)
has a real solution.
The corresponding 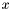 -coordinates of these points satisfies
-coordinates of these points satisfies 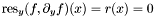 . We solve this equation. Let
. We solve this equation. Let 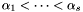 be the real roots of
be the real roots of 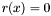 . For each
. For each 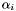 , we \ compute the corresponding
, we \ compute the corresponding 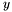 such that
such that 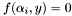 . At this point, we also check that the curve is in generic position, that is, there is at most one multiple solution of
. At this point, we also check that the curve is in generic position, that is, there is at most one multiple solution of 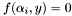 .
.
Once these points are computed, we compute intermediate (rational) points 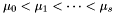 , such that
, such that 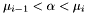 and the corresponding
and the corresponding 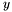 such that
such that 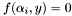 .
.
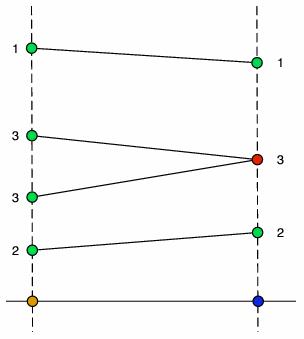
All these points are collected and sorted by lexicographic order such that 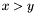 . The subset of points, corresponding to two consecutive
. The subset of points, corresponding to two consecutive 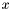 -coordinates are connected, according to their
-coordinates are connected, according to their 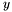 -coordinates, in the order described below:
-coordinates, in the order described below:
void topology::assign(topology::point_graph<C>& g, const MPol<U>& p,TopSweep2d<C,SLV> mth);
g (of type topology::point_graph<C>) which is isotopic to the curve 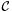 , defined by the polynomial
, defined by the polynomial p. The coefficients of the points in the graph are of type C. The polynomial P is converted to a polynomial with rational coefficients, if needed.TopSweep2d depends on two parameters:C, which is the type of coefficients of the points in the result,SLV, which is the type of univariate solver to be used. The default value for SLV is Aberth<RR>.
typedef u_solution_t; the type of the solutions which are computed by the solver,static Seq<u_solution_t> u_solve( const UPOL& p); which specifies the univariate solver, used in the algorithm.![]()
![]()
#include <cstdio> #include <synaps/arithm/gmp.h> #include <synaps/topology/TopSweep2d.h> int main(int argc, char** argv) { const char * exemples[] = { "33481-68244*x+47684*y+32162*x^2-54873*x*y+86*x^3*y+2566*x^3+3974*y^4*x+1354*x^2*y^3+13464*y^3-14150*y^4+4622*y^5+37086*y^2*x+7078*x^2*y-6980*y^3*x+204*x^2*y^2+34*x^4+267*x^3*y^2+x^5-y^7-21*x*y^5+25*x^4*y-30*y^6-37557*y^2", "x^6+y^2*x^4-y^4*x^2-2*x^4-y^6+2*y^4+x^2-y^2+x*y" }; for ( int i = 0; i < 2; i ++ ) { std::cout << i << std::endl; MPol<QQ> p(exemples[i], Variables("x y")); topology::point_graph<double> g; topology::assign(g, p, TopSweep2d<double>()); char file[200]; sprintf(file,"tmp-%i.off",i); geomview::ostream vw(file); vw<<g; vw.view(); }; return 0; }
Here is the graph,which is computed:
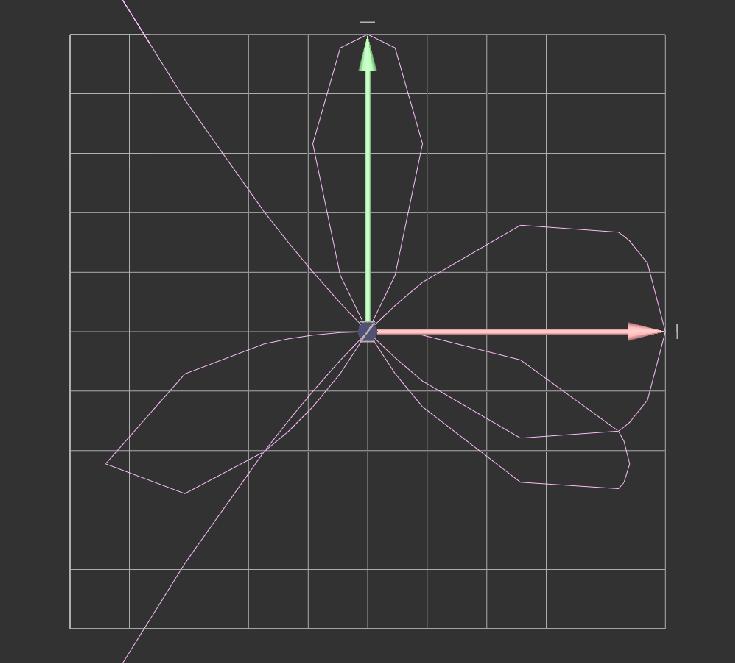
 |