![\[ p \assign x_{}^3 + 28 x_{} + 23 \]](form_518.png)
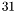 :
: typedef UPolDse<Z<31> > upol_t;
#include <synaps/arithm/Zp.h> //modular arithmetic #include <synaps/upol.h> //univariate polynomials
upol_t p("x^3-34*x+23");
![\[ p \assign x_{}^3 + 28 x_{} + 23 \]](form_518.png)
For univariate polynomials, the variables 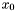 and
and 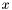 are equal. The natural operations of polynomials are available. For instance,
are equal. The natural operations of polynomials are available. For instance,
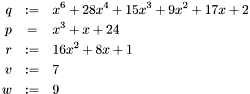
Notice that the operator % compute the remainder of the Euclidean division if the leading term is invertible (here it is the case since 31 is prime). The quotient is given by the operator /. For more details on the available operators see synaps/upol/UPolDse.h.
![]()
![]()
#include <synaps/arithm/Zp.h> #include <synaps/upol.h> typedef UPolDse< Z<31> > upol_t; int main(int argc, char** argv) { using std::cout; using std::endl; upol_t p("x^3-34*x+23"); cout<< p <<endl; upol_t q = p*p; cout<< q <<endl; p += upol_t("4*x+32"); cout<< p <<endl; upol_t r = q%p; cout<< r <<endl; Z<31> v = q(Z<31>(1)); cout<< v <<endl; }
Exercise: Build a function Wilkinson which given 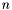 computes computes ![$W_n (x) = \prod_1^n (x - i) \in \mathbbm{Q}[x]$](form_520.png)  |
Instead of using the monomial basis, one might be interested by using coefficients in another basis, eg. the Bernstein basis. In order to manipulate such representations, one has only to change the container:
typedef UPolDse<double, bezier::rep1d<double> > upolb_t;
#include <synaps/upol/bezier/rep1d.h>
![$[0, 1]$](form_180.png) .
. upolb_t b1("x^2+1"), b2("x"), b3; VECTOR::print(cout,b1)<<endl; //b1 printed as a vector of coefficients VECTOR::print(cout,b2)<<endl; //b2 printed as a vector of coefficients b3 = b1*b2; VECTOR::print(cout,b3)<<endl; //b3 printed as a vector of coefficients
![\begin{eqnarray*} & [1, 1, 2] & (\tmop{coefficients} \tmop{of} b_1 \tmop{in} \tmop{the} \tmop{Bernstein} \tmop{basis} \tmop{on} [0, 1])\\ & [0, 1] & (\tmop{coefficients} \tmop{of} b_2 \tmop{in} \tmop{the} \tmop{Bernstein} \tmop{basis} \tmop{on} [0, 1])\\ & b_3 \assign x^3 + x & \\ & [0, 0.333333, 0.666667, 2] & (\tmop{coefficients} \tmop{of} b_3 \tmop{in} \tmop{the} \tmop{Bernstein} \tmop{basis} \tmop{on} [0, 1]) \end{eqnarray*}](form_521.png)
Notice that even if the coefficients of 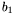 and
and 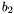 are integers, the coefficients of
are integers, the coefficients of 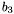 are not. {{When we use the Bernstein representation, the coefficient type of UPolDse should be a field type}}.
are not. {{When we use the Bernstein representation, the coefficient type of UPolDse should be a field type}}.
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include <synaps/arithm/Zp.h> #include <synaps/upol.h> #include "synaps/arithm/gmp.h" #include <synaps/upol/bezier/rep1d.h> typedef UPolDse<double, bezier::rep1d<double> > upolb_t; int main(int argc, char** argv) { using std::cout; using std::endl; upolb_t b1("x^2+1"), b2("x"), b3; VECTOR::print(cout,b1)<<endl; VECTOR::print(cout,b2)<<endl; b3 = b1*b2; cout <<b3<<endl; VECTOR::print(cout,b3)<<endl; } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
typedef MPol<QQ> mpol_t;
#include <synaps/arithm/gmp.h> //big numbers #include <synaps/mpol.h> //multivariate polynomials
typedef MPol<QQ,DegLex,std::list<Monom<ZZ,dynamicexp<unsigned> > > > mpol_t;
synaps/mpol/MPol.h .They share, with the univariate polynomials, algebraic operators such as addition, multiplication, ... They can also be constructed from strings. The following examples
mpol_t a("x1^2*x0+2*x1+3;"), b("x1^2+123*x2;"); a *= b;
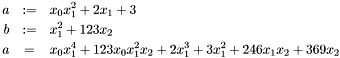
Iterators are available to scan a multivariate polynomial, as it is illustrate now:
VECTOR::print(cout,a)<<endl; for(mpol_t::iterator it =a.begin(); it !=a.end();it++) cout<< it->coeff()<<" "; cout<< endl; for(mpol_t::iterator it =a.begin(); it !=a.end();it++) it->coeff()*=it->coeff(); cout<< a <<endl;
![\[ [x_0 x_1^4, 123 x_0 x_1^2 x_2, 2 x_1^3, 3 x_1^2, 246 x_1 x_2, 369 x_2] \]](form_526.png)
(that is the list of monomials printed as a vector of monomials)
![\[ 1 123 2 3 246 369 \]](form_527.png)
(that is the list of coefficients of the monomials)
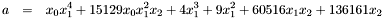
(that is the polynomial with the coefficients squared).
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include "synaps/arithm/QQ.h" #include "synaps/mpol.h" typedef MPol<QQ> mpol_t; int main(int argc, char** argv) { using std::cout; using std::endl; mpol_t a("x1^2*x0+2*x1+3"), b("x1^2+123*x2"); a *= b; cout<<a<<endl; VECTOR::print(cout,a)<<endl; for(mpol_t::iterator it=a.begin(); it !=a.end(); it++) cout<<it->coeff()<<" "; cout<<endl; for(mpol_t::iterator it =a.begin(); it !=a.end();it++) it->coeff()*=it->coeff(); cout<<a<<endl; } #else int main(int argc, char** argv) {} #endif //SYNAPS_WITH_GMP
Exercise: Define a function shifteval which given a multivariate polynomial  (s,t) (with (s,t) (with  and a value and a value 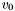 of type double, compute the mutlivariate polynomial of type double, compute the mutlivariate polynomial 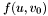 (with (with 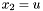 ) )  |
#include <synaps/mpol/MPolDse.h>
We need a new interface (not just a new container) since the concept of exponents is not attached to this class. Here are some examples, using the Bernstein basis:
#include <synaps/arithm/gmp.h> typedef MPolDse<QQ, MPOLDSE::bernstein<QQ> > mpolb_t;
mpolb_t A("x1^2*x0+2*x1+3"), B("x0+x1+1"), C=A*B; VECTOR::print(cout,A.rep())<<endl; VECTOR::print(cout,B.rep())<<endl; VECTOR::print(cout,C.rep())<<endl;
![\begin{eqnarray*} & & [3, 3, 4, 4, 5, 6]\\ & & [1, 2, 2, 3]\\ C & \assign & x_0^2 x_1^2 + x_0 x_1^3 + x_0 x_1^2 + 2 x_0 x_1 + 2 x_1^2 + 3 x_0 + 5 x_1 + 3\\ & & [3, \frac{14}{3}, 7, 10, \frac{9}{2}, \frac{13}{2}, \frac{28}{3}, \frac{27}{2}, 6, \frac{25}{3}, 12, 18] \end{eqnarray*}](form_535.png)
{{Here also, the coefficient type of MPolDse should be a field type, when we use the Bernstein representation}}.
The default construction
typedef MPolDse<double> mpold_t;
![]()
![]()
#include <synaps/init.h> #ifdef SYNAPS_WITH_GMP #include "synaps/arithm/gmp.h" #include "synaps/mpol.h" #include "synaps/mpol/MPolDse.h" typedef MPolDse<QQ> mpold_t; typedef MPolDse<QQ, mpoldse::bernstein<QQ> > mpolb_t; int main(int argc, char** argv) { using std::cout; using std::endl; mpolb_t A("x1^2*x0+2*x1+3"),B("x0+x1+1"),C=A*B; VECTOR::print(cout,A.rep())<<endl; VECTOR::print(cout,B.rep())<<endl; VECTOR::print(cout,C.rep())<<endl; std::cout<<C<<std::endl; } #else int main(int argc, char** argv) {} #endif
 |