R is upol::rep<C>. The corresponding basis used to store the polynomial is the monomial bais 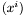 .
.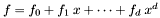 is represented by an array of coefficients
is represented by an array of coefficients ![$[f_0, \ldots, f_d]$](form_101.png) . All its coefficients are stored. It is assumed here that the coefficient ring has the basic arithmetic operations.
. All its coefficients are stored. It is assumed here that the coefficient ring has the basic arithmetic operations.The implementation is parameterised as follows:
template<class C, class R=upol::rep<C> > struct UPolDse;
where
C is the coefficient type.R corresponds to the internal representation.R is upol::rep<C>. The corresponding basis used to store the polynomial is the monomial bais 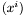 .
.std::vector<C> of the {stl} can also be used. Here also, we use the monomial basis.bezier::rep1d<C> (see synaps/upol/bezier/rep1d.h). In this case, it is assumed the polynomial is represented in the Bernstein basis 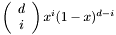 , if it is of degree
, if it is of degree 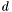 . When a polynomial is constructed for a string (eg.
. When a polynomial is constructed for a string (eg. x\^{ 2+x-1}), the conversion from the monomial basis to the Bersntein basis is performed. When the polynomial is printed, the converse transformation is applied.UPOLDAR.
synaps/upol/UPolDse.h, synaps/upol/UPOLDAR.m![]()
![]()
#include <complex> #include <synaps/upol.h> #include <synaps/upol/bezier/rep1d.h> typedef UPolDse<double> upol_t; typedef UPolDse<double,bezier::rep1d<double> > bpol_t; int main (int argc, char **argv) { using std::cout; using std::endl; upol_t p0("x^2+x+1"); double u1[]={2,0,-1,1}; upol_t p1(u1,u1+4); cout <<"p0 = "<<p0<<", p1 = "<<p1<<endl; //| p 0 = x^2 + x + 1, p 1 = x^3 - x^2 + 2 //| The variable is x. cout<<"p0(complex(0,1)) ="<<p0(std::complex<double>(0,1))<<endl; //| p0 ( ( 0, 1 ) ) = (0,1) cout<<"p1(1) ="<<p1(1.)<<endl; //| p1 (1) = 2 upol_t p2(p0+p1); cout<<p2<<endl; //| x^3 + x + 3 p2=p0-p1; cout<<p2<<endl; //| - x^3 + 2*x^2 + x - 1 p2=p0*p1; cout<<p2<<endl; //| x^5 + x^2 + 2 x + 2 p2+=p1-p0; cout<<p2<<endl; //| x^5 + x^3 - x^2 + x + 3 p2=(p1+p0)*(p1-p0*2); cout<<p2<<endl; //| x^6 - 3*x^5 - x^4 - 11*x^2 - 6*x p2=p1/p0; cout<<p2<<endl; //Quotient in the Euclidean division //| x - 2 p2=p1%p0; cout<<p2<<endl; //Remainder in the Euclidean division //| x + 4 bpol_t b0("x^2+x+1"); bpol_t b1(u1,u1+4); cout <<"b0 = "<<b0<<", b1 = "<<b1<<endl; //| b0 = 1*x^2+1*x+1, b1 = 2*x^3+3*x^2-6*x+2 cout<<"b0(comblex(0,1)) ="<<b0(std::complex<double>(0,1))<<endl; //| b0 ( ( 0, 1 ) ) = (0,1) cout<<"b1(1) ="<<b1(1.)<<endl; //| b1 (1) = 2 // Same operations and results with the Bernstein basis // representation. bpol_t b2(b0+b1); b2=b0-b1; b2=b0*b1; b2+=b1-b0; b2=(b1+b0)*(b1-b0*2); }
content(p) computes the gcd of the coefficients of p. If their type is double, it returns the leading coefficient for non-zero polynomials and 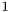 otherwise.
otherwise.gcd(p,q) computes the gcd of two polynomials. It is based on the Sturm-Habicht construction. The content of the returned polynomial is 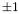 .
.lcm(p,q) computes the squarefree part of a polynomial 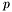 , that is
, that is 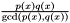 .
. synaps/upol/gcd.hsquare_free(p) computes the squarefree part of a polynomial 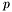 , that is
, that is 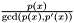 .
.square_free_factorisation(p) computes the product of factors of multiplicity 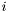 in
in 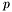 . It outputs a sequence of polynomials, the
. It outputs a sequence of polynomials, the 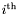 polynomial corresponding to the factors of multiplicity
polynomial corresponding to the factors of multiplicity 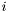 .
.synaps/upol/square_free.h  |